Question
A cuboid has a rectangular base of width \(x\) cm and length 2\(x\) cm . The height of the cuboid is \(h\) cm . The total length of the edges of the cuboid is \(72\) cm.
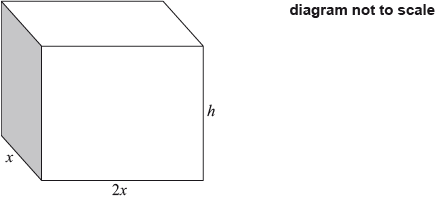
The volume, \(V\), of the cuboid can be expressed as \(V = a{x^2} – 6{x^3}\).
Find the value of \(a\).[3]
Find the value of \(x\) that makes the volume a maximum.[3]
Answer/Explanation
Markscheme
\(72 = 12x + 4h\;\;\;\)(or equivalent) (M1)
Note: Award (M1) for a correct equation obtained from the total length of the edges.
\(V = 2{x^2}(18 – 3x)\) (A1)
\((a = ){\text{ }}36\) (A1) (C3)
\(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 72x – 18{x^2}\) (A1)
\(72x – 18{x^2} = 0\;\;\;\)OR\(\;\;\;\frac{{{\text{d}}V}}{{{\text{d}}x}} = 0\) (M1)
Notes: Award (A1) for \( – 18{x^2}\) seen. Award (M1) for equating derivative to zero.
\((x = ){\text{ 4}}\) (A1)(ft) (C3)
Note: Follow through from part (a).
OR
Sketch of \(V\) with visible maximum (M1)
Sketch with \(x \geqslant 0,{\text{ }}V \geqslant 0\) and indication of maximum (e.g. coordinates) (A1)(ft)
\((x = ){\text{ 4}}\) (A1)(ft) (C3)
Notes: Follow through from part (a).
Award (M1)(A1)(A0) for \((4,{\text{ }}192)\).
Award (C3) for \(x = 4,{\text{ }}y = 192\).
Question
A company sells fruit juices in cylindrical cans, each of which has a volume of \(340\,{\text{c}}{{\text{m}}^3}\). The surface area of a can is \(A\,{\text{c}}{{\text{m}}^2}\) and is given by the formula
\(A = 2\pi {r^2} + \frac{{680}}{r}\) ,
where \(r\) is the radius of the can, in \({\text{cm}}\).
To reduce the cost of a can, its surface area must be minimized.
Find \(\frac{{{\text{d}}A}}{{{\text{d}}r}}\)[3]
Calculate the value of \(r\) that minimizes the surface area of a can.[3]
Answer/Explanation
Markscheme
\(\left( {\frac{{{\text{d}}A}}{{{\text{d}}r}}} \right) = 4\pi r – \frac{{680}}{{{r^2}}}\) (A1)(A1)(A1) (C3)
Note: Award (A1) for \(4\pi r\) (accept \(12.6r\)), (A1) for \( – 680\), (A1) for \(\frac{1}{{{r^2}}}\) or \({r^{ – 2}}\)
Award at most (A1)(A1)(A0) if additional terms are seen.
\(4\pi r – \frac{{680}}{{{r^2}}} = 0\) (M1)
Note: Award (M1) for equating their \(\frac{{{\text{d}}A}}{{{\text{d}}r}}\) to zero.
\(4\pi {r^3} – 680 = 0\) (M1)
Note: Award (M1) for initial correct rearrangement of the equation. This may be assumed if \({r^3} = \frac{{680}}{{4\pi }}\) or \(r = \sqrt[3]{{\frac{{680}}{{4\pi }}}}\) seen.
OR
sketch of \(A\) with some indication of minimum point (M1)(M1)
Note: Award (M1) for sketch of \(A\), (M1) for indication of minimum point.
OR
sketch of \(\frac{{{\text{d}}A}}{{{\text{d}}r}}\) with some indication of zero (M1)(M1)
Note: Award (M1) for sketch of \(\frac{{{\text{d}}A}}{{{\text{d}}r}}\), (M1) for indication of zero.
\((r = )\,\,3.78\,({\text{cm}})\,\,\,\,\,(3.78239…)\) (A1)(ft) (C3)
Note: Follow through from part (a).
Question
Maria owns a cheese factory. The amount of cheese, in kilograms, Maria sells in one week, \(Q\), is given by
\(Q = 882 – 45p\),
where \(p\) is the price of a kilogram of cheese in euros (EUR).
Maria earns \((p – 6.80){\text{ EUR}}\) for each kilogram of cheese sold.
To calculate her weekly profit \(W\), in EUR, Maria multiplies the amount of cheese she sells by the amount she earns per kilogram.
Write down how many kilograms of cheese Maria sells in one week if the price of a kilogram of cheese is 8 EUR.[1]
Find how much Maria earns in one week, from selling cheese, if the price of a kilogram of cheese is 8 EUR.[2]
Write down an expression for \(W\) in terms of \(p\).[1]
Find the price, \(p\), that will give Maria the highest weekly profit.[2]
Answer/Explanation
Markscheme
522 (kg) (A1) (C1)[1 mark]
\(522(8 – 6.80)\) or equivalent (M1)
Note: Award (M1) for multiplying their answer to part (a) by \((8 – 6.80)\).
626 (EUR) (626.40) (A1)(ft) (C2)
Note: Follow through from part (a).[2 marks]
\((W = ){\text{ }}(882 – 45p)(p – 6.80)\) (A1)
OR
\((W = ) – 45{p^2} + 1188p – 5997.6\) (A1) (C1)[1 mark]
sketch of \(W\) with some indication of the maximum (M1)
OR
\( – 90p + 1188 = 0\) (M1)
Note: Award (M1) for equating the correct derivative of their part (c) to zero.
OR
\((p = ){\text{ }}\frac{{ – 1188}}{{2 \times ( – 45)}}\) (M1)
Note: Award (M1) for correct substitution into the formula for axis of symmetry.
\((p = ){\text{ }}13.2{\text{ (EUR)}}\) (A1)(ft) (C2)
Note: Follow through from their part (c), if the value of \(p\) is such that \(6.80 < p < 19.6\).[2 marks]
Question
A factory produces shirts. The cost, C, in Fijian dollars (FJD), of producing x shirts can be modelled by
C(x) = (x − 75)2 + 100.
The cost of production should not exceed 500 FJD. To do this the factory needs to produce at least 55 shirts and at most s shirts.
Find the cost of producing 70 shirts.[2]
Find the value of s.[2]
Find the number of shirts produced when the cost of production is lowest.[2]
Answer/Explanation
Markscheme
(70 − 75)2 + 100 (M1)
Note: Award (M1) for substituting in x = 70.
125 (A1) (C2)[2 marks]
(s − 75)2 + 100 = 500 (M1)
Note: Award (M1) for equating C(x) to 500. Accept an inequality instead of =.
OR
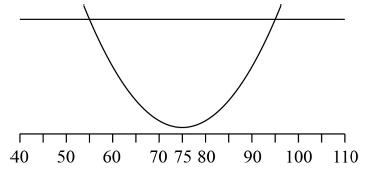 (M1)
(M1)
Note: Award (M1) for sketching correct graph(s).
(s =) 95 (A1) (C2)[2 marks]
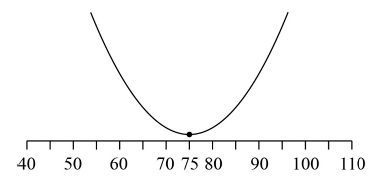 (M1)
(M1)
Note: Award (M1) for an attempt at finding the minimum point using graph.
OR
\(\frac{{95 + 55}}{2}\) (M1)
Note: Award (M1) for attempting to find the mid-point between their part (b) and 55.
OR
(C’(x) =) 2x − 150 = 0 (M1)
Note: Award (M1) for an attempt at differentiation that is correctly equated to zero.
75 (A1) (C2)[2 marks]
Question
A small manufacturing company makes and sells \(x\) machines each month. The monthly cost \(C\) , in dollars, of making \(x\) machines is given by
\[C(x) = 2600 + 0.4{x^2}{\text{.}}\]The monthly income \(I\) , in dollars, obtained by selling \(x\) machines is given by
\[I(x) = 150x – 0.6{x^2}{\text{.}}\]\(P(x)\) is the monthly profit obtained by selling \(x\) machines.
Find \(P(x)\) .[2]
Find the number of machines that should be made and sold each month to maximize \(P(x)\) .[2]
Use your answer to part (b) to find the selling price of each machine in order to maximize \(P(x)\) .[2]
Answer/Explanation
Markscheme
\(P(x) = I(x) – C(x)\) (M1)
\( = – {x^2} + 150x – 2600\) (A1) (C2)
\( – 2x + 150 = 0\) (M1)
Note: Award (M1) for setting \(P'(x) = 0\) .
OR
Award (M1) for sketch of \(P(x)\) and maximum point identified. (M1)
\(x = 75\) (A1)(ft) (C2)
Note: Follow through from their answer to part (a).
\(\frac{{7875}}{{75}}\) (M1)
Note: Award (M1) for \(7875\) seen.
\( = 105\) (A1)(ft) (C2)
Note: Follow through from their answer to part (b).

