Download IITian Academy App for accessing Online Mock Tests and More..
Question
Expand \(\sum\limits_{r = 4}^7 {{2^r}} \) as the sum of four terms.
(i) Find the value of \(\sum\limits_{r = 4}^{30} {{2^r}} \) .
(ii) Explain why \(\sum\limits_{r = 4}^\infty {{2^r}} \) cannot be evaluated.
Answer/Explanation
Markscheme
\(\sum\limits_{r = 4}^7 {{2^r}} = {2^4} + {2^5} + {2^6} + {2^7}\) (accept \(16 + 32 + 64 + 128\) ) A1 N1
[1 mark]
(i) METHOD 1
recognizing a GP (M1)
\({u_1} = {2^4}\) , \(r = 2\) , \(n = 27\) (A1)
correct substitution into formula for sum (A1)
e.g. \({S_{27}} = \frac{{{2^4}({2^{27}} – 1)}}{{2 – 1}}\)
\({S_{27}} = 2147483632\) A1 N4
METHOD 2
recognizing \(\sum\limits_{r = 4}^{30} { = \sum\limits_{r = 1}^{30} { – \sum\limits_{r = 1}^3 {} } } \) (M1)
recognizing GP with \({u_1} = 2\) , \(r = 2\) , \(n = 30\) (A1)
correct substitution into formula for sum
\({S_{30}} = \frac{{2({2^{30}} – 1)}}{{2 – 1}}\) (A1)
\( = 214783646\)
\(\sum\limits_{r = 4}^{30} {{2^r}} = 2147483646 – (2 + 4 + 8)\)
\( = 2147483632\) A1 N4
(ii) valid reason (e.g. infinite GP, diverging series), and \(r \ge 1\) (accept \(r > 1\) ) R1R1 N2
[6 marks]
Question
Ten students were surveyed about the number of hours, \(x\), they spent browsing the Internet during week 1 of the school year. The results of the survey are given below.
\[\sum\limits_{i = 1}^{10} {{x_i} = 252,{\text{ }}\sigma = 5{\text{ and median}} = 27.} \]
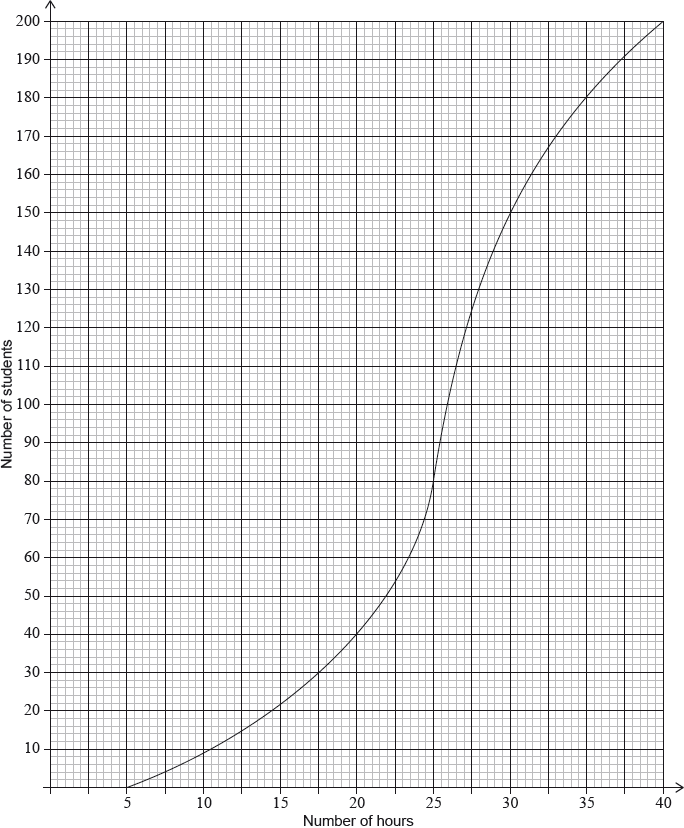
During week 4, the survey was extended to all 200 students in the school. The results are shown in the cumulative frequency graph:
Find the mean number of hours spent browsing the Internet.
During week 2, the students worked on a major project and they each spent an additional five hours browsing the Internet. For week 2, write down
(i) the mean;
(ii) the standard deviation.
During week 3 each student spent 5% less time browsing the Internet than during week 1. For week 3, find
(i) the median;
(ii) the variance.
(i) Find the number of students who spent between 25 and 30 hours browsing the Internet.
(ii) Given that 10% of the students spent more than k hours browsing the Internet, find the maximum value of \(k\).
Answer/Explanation
Markscheme
attempt to substitute into formula for mean (M1)
eg\(\,\,\,\,\,\)\(\frac{{\Sigma x}}{{10}},{\text{ }}\frac{{252}}{n},{\text{ }}\frac{{252}}{{10}}\)
mean \( = 25.2{\text{ (hours)}}\) A1 N2
[2 marks]
(i) mean \( = 30.2{\text{ (hours)}}\) A1 N1
(ii) \(\sigma = 5{\text{ (hours)}}\) A1 N1
[2 marks]
(i) valid approach (M1)
eg\(\,\,\,\,\,\)95%, 5% of 27
correct working (A1)
eg\(\,\,\,\,\,\)\(0.95 \times 27,{\text{ }}27 – (5\% {\text{ of }}27)\)
median \( = 25.65{\text{ (exact), }}25.7{\text{ (hours)}}\) A1 N2
(ii) METHOD 1
variance \( = {({\text{standard deviation}})^2}\) (seen anywhere) (A1)
valid attempt to find new standard deviation (M1)
eg\(\,\,\,\,\,\)\({\sigma _{new}} = 0.95 \times 5,{\text{ }}4.75\)
variance \( = 22.5625{\text{ }}({\text{exact}}),{\text{ }}22.6\) A1 N2
METHOD 2
variance \( = {({\text{standard deviation}})^2}\) (seen anywhere) (A1)
valid attempt to find new variance (M1)
eg\(\,\,\,\,\,\)\({0.95^2}{\text{ }},{\text{ }}0.9025 \times {\sigma ^2}\)
new variance \( = 22.5625{\text{ }}({\text{exact}}),{\text{ }}22.6\) A1 N2
[6 marks]
(i) both correct frequencies (A1)
eg\(\,\,\,\,\,\)80, 150
subtracting their frequencies in either order (M1)
eg\(\,\,\,\,\,\)\(150 – 80,{\text{ }}80 – 150\)
70 (students) A1 N2
(ii) evidence of a valid approach (M1)
eg\(\,\,\,\,\,\)10% of 200, 90%
correct working (A1)
eg\(\,\,\,\,\,\)\(0.90 \times 200,{\text{ }}200 – 20\), 180 students
\(k = 35\) A1 N3
[6 marks]
Question
Let \(f\left( x \right) = {{\text{e}}^{2\,{\text{sin}}\left( {\frac{{\pi x}}{2}} \right)}}\), for x > 0.
The k th maximum point on the graph of f has x-coordinate xk where \(k \in {\mathbb{Z}^ + }\).
Given that xk + 1 = xk + a, find a.
Hence find the value of n such that \(\sum\limits_{k = 1}^n {{x_k} = 861} \).
Answer/Explanation
Markscheme
valid approach to find maxima (M1)
eg one correct value of xk, sketch of f
any two correct consecutive values of xk (A1)(A1)
eg x1 = 1, x2 = 5
a = 4 A1 N3
[4 marks]
recognizing the sequence x1, x2, x3, …, xn is arithmetic (M1)
eg d = 4
correct expression for sum (A1)
eg \(\frac{n}{2}\left( {2\left( 1 \right) + 4\left( {n – 1} \right)} \right)\)
valid attempt to solve for n (M1)
eg graph, 2n2 − n − 861 = 0
n = 21 A1 N2
[4 marks]