Question
A graph G with vertices A, B, C, D, E has the following cost adjacency table.
\[\begin{array}{*{20}{c|ccccc}}
{}&{\text{A}}&{\text{B}}&{\text{C}}&{\text{D}}&{\text{E}} \\
\hline
{\text{A}}& – &{12}&{10}&{17}&{19} \\
{\text{B}}&{12}& – &{13}&{20}&{11} \\
{\text{C}}&{10}&{13}& – &{16}&{14} \\
{\text{D}}&{17}&{20}&{16}& – &{15} \\
{\text{E}}&{19}&{11}&{14}&{15}& –
\end{array}\]
(a) (i) Use Kruskal’s algorithm to find and draw the minimum spanning tree for G.
(ii) The graph H is formed from G by removing the vertex D and all the edges connected to D. Draw the minimum spanning tree for H and use it to find a lower bound for the travelling salesman problem for G.
(b) Show that 80 is an upper bound for this travelling salesman problem.
Answer/Explanation
Markscheme
(a) (i) the edges are joined in the order
AC
BE
AB
ED A2
 A1
A1
Note: Final A1 independent of the previous A2.
(ii)
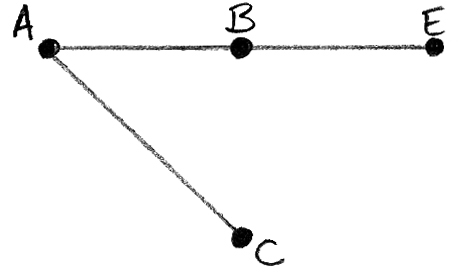 A1
A1
the weight of this spanning tree is 33 A1
to find a lower bound for the travelling salesman problem, we add to that the two smallest weights of edges to D, i.e. 15 +16, giving 64 M1A1
[7 marks]
(b) an upper bound is the weight of any Hamiltonian cycle, e.g. ABCDEA has weight 75 so 80 is certainly an upper bound M1A1
[2 marks]
Total [9 marks]
Examiners report
Part (a) was well done by many candidates although some candidates simply drew the minimum spanning tree in (i) without indicating the use of Kruskal’s Algorithm. It is important to stress to candidates that, as indicated in the rubric at the top of Page 2, answers must be supported by working and/or explanations. Part (b) caused problems for some candidates who obtained the unhelpful upper bound of 96 by doubling the weight of the minimum spanning tree. It is useful to note that the weight of any Hamiltonian cycle is an upper bound and in this case it was fairly easy to find such a cycle with weight less than or equal to 80.
Question
Mathilde delivers books to five libraries, A, B, C, D and E. She starts her deliveries at library D and travels to each of the other libraries once, before returning to library D. Mathilde wishes to keep her travelling distance to a minimum.
The weighted graph \(H\), representing the distances, measured in kilometres, between the five libraries, has the following table.
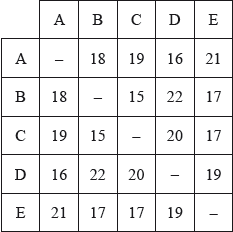
Draw the weighted graph \(H\).
Starting at library D use the nearest-neighbour algorithm, to find an upper bound for Mathilde’s minimum travelling distance. Indicate clearly the order in which the edges are selected.
By first removing library C, use the deleted vertex algorithm, to find a lower bound for Mathilde’s minimum travelling distance.
Answer/Explanation
Markscheme
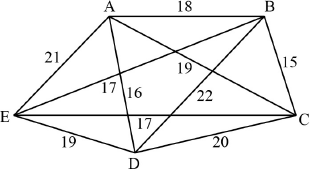
complete graph on 5 vertices A1
weights correctly marked on graph A1
[2 marks]
clear indication that the nearest-neighbour algorithm has been applied M1
DA (or 16) A1
AB (or 18) then BC (or 15) A1
CE (or 17) then ED (or 19) A1
\({\text{UB}} = 85\) A1
[5 marks]
an attempt to find the minimum spanning tree (M1)
DA (16) then BE (17) then AB (18) (total 51) A1
reconnect C with the two edges of least weight, namely CB (15) and CE (17) M1
\({\text{LB}} = 83\) A1
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
Consider the following weighted graph G.
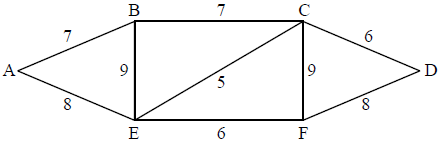
State what feature of G ensures that G has an Eulerian trail.
State what feature of G ensures that G does not have an Eulerian circuit.
Write down an Eulerian trail in G.
State the Chinese postman problem.
Starting and finishing at B, find a solution to the Chinese postman problem for G.
Calculate the total weight of the solution.
Answer/Explanation
Markscheme
G has an Eulerian trail because it has (exactly) two vertices (B and F) of odd degree R1
[1 mark]
G does not have an Eulerian circuit because not all vertices are of even degree R1
[1 mark]
for example BAEBCEFCDF A1A1
Note: Award A1 for start/finish at B/F, A1 for the middle vertices.
[2 marks]
to determine the shortest route (walk) around a weighted graph A1
using each edge (at least once, returning to the starting vertex) A1
Note: Correct terminology must be seen. Do not accept trail, path, cycle or circuit.
[2 marks]
we require the Eulerian trail in (b), (weight = 65) (M1)
and the minimum walk FEB (15) A1
for example BAEBCEFCDFEB A1
Note: Accept EB added to the end or FE added to the start of their answer in (b) in particular for follow through.
[3 marks]
total weight is (65 + 15=)80 A1
[1 mark]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
The weights of the edges of a graph G with vertices A, B, C, D and E are given in the following table.
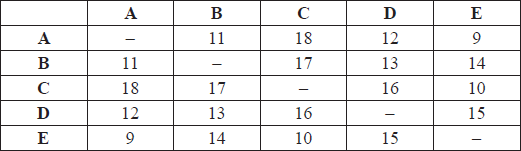
Starting at A, use the nearest neighbour algorithm to find an upper bound for the travelling salesman problem for G .
(i) Use Kruskal’s algorithm to find and draw a minimum spanning tree for the subgraph obtained by removing the vertex A from G .
(ii) Hence use the deleted vertex algorithm to find a lower bound for the travelling salesman problem for G .
Answer/Explanation
Markscheme
using the nearest neighbour algorithm, starting with A,
\({\text{A}} \to {\text{E, E}} \to {\text{C}}\) A1
\({\text{C}} \to {\text{D, D}} \to {\text{B}}\) A1
\({\text{B}} \to {\text{A}}\) A1
the upper bound is therefore 9 + 10 + 16 + 13 + 11 = 59 A1
[4 marks]
(i) the edges are added in the order CE A1
BD A1
BE A1
 A1
A1
(ii) the weight of the minimum spanning tree is 37 (A1)
we now reconnect A with the 2 edges of least weight (M1)
i.e. AE and AB A1
the lower bound is therefore 37 + 9 + 11 = 57 A1
[8 marks]
Examiners report
[N/A]
[N/A]

