Download IITian Academy App for accessing Online Mock Tests and More..
Question
Mathilde delivers books to five libraries, A, B, C, D and E. She starts her deliveries at library D and travels to each of the other libraries once, before returning to library D. Mathilde wishes to keep her travelling distance to a minimum.
The weighted graph \(H\), representing the distances, measured in kilometres, between the five libraries, has the following table.
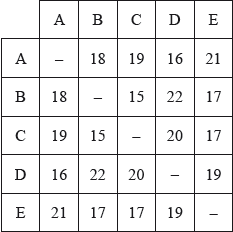
Draw the weighted graph \(H\).
Starting at library D use the nearest-neighbour algorithm, to find an upper bound for Mathilde’s minimum travelling distance. Indicate clearly the order in which the edges are selected.
By first removing library C, use the deleted vertex algorithm, to find a lower bound for Mathilde’s minimum travelling distance.
Answer/Explanation
Markscheme
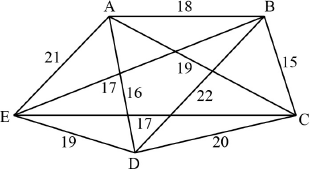
complete graph on 5 vertices A1
weights correctly marked on graph A1
[2 marks]
clear indication that the nearest-neighbour algorithm has been applied M1
DA (or 16) A1
AB (or 18) then BC (or 15) A1
CE (or 17) then ED (or 19) A1
\({\text{UB}} = 85\) A1
[5 marks]
an attempt to find the minimum spanning tree (M1)
DA (16) then BE (17) then AB (18) (total 51) A1
reconnect C with the two edges of least weight, namely CB (15) and CE (17) M1
\({\text{LB}} = 83\) A1
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
Consider the following weighted graph G.
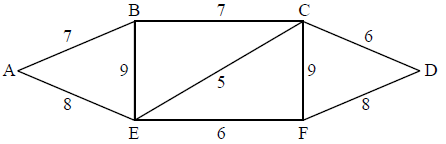
State what feature of G ensures that G has an Eulerian trail.
State what feature of G ensures that G does not have an Eulerian circuit.
Write down an Eulerian trail in G.
State the Chinese postman problem.
Starting and finishing at B, find a solution to the Chinese postman problem for G.
Calculate the total weight of the solution.
Answer/Explanation
Markscheme
G has an Eulerian trail because it has (exactly) two vertices (B and F) of odd degree R1
[1 mark]
G does not have an Eulerian circuit because not all vertices are of even degree R1
[1 mark]
for example BAEBCEFCDF A1A1
Note: Award A1 for start/finish at B/F, A1 for the middle vertices.
[2 marks]
to determine the shortest route (walk) around a weighted graph A1
using each edge (at least once, returning to the starting vertex) A1
Note: Correct terminology must be seen. Do not accept trail, path, cycle or circuit.
[2 marks]
we require the Eulerian trail in (b), (weight = 65) (M1)
and the minimum walk FEB (15) A1
for example BAEBCEFCDFEB A1
Note: Accept EB added to the end or FE added to the start of their answer in (b) in particular for follow through.
[3 marks]
total weight is (65 + 15=)80 A1
[1 mark]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]