Question
a.Use the Euclidean algorithm to express gcd (123, 2347) in the form 123p + 2347q, where \(p,{\text{ }}q \in \mathbb{Z}\).[8]
b.Find the least positive solution of \(123x \equiv 1(\bmod 2347)\) .[3]
c.Find the general solution of \(123z \equiv 5(\bmod 2347)\) .[3]
d.State the solution set of \(123y \equiv 1(\bmod 2346)\) .[1]
▶️Answer/Explanation
Markscheme
\(2347 = 19 \times 123 + 10\) M1A1
\((123 = 12 \times 10 + 3)\)
\(10 = 3 \times 3 + 1\) A1
\(1(\gcd ) = 10 – 3 \times 3 = 10 – 3 \times (123 – 12 \times 10)\) M1A1
\( = 37 \times 10 – 3 \times 123\) A1
\( = 37 \times (2347 – 19 \times 123) – 3 \times 123\) (for continuation) M1
\( = 37 \times 2347 – 706 \times 123\) A1
[8 marks]
EITHER
\(1(\bmod 2347) = ( – 706 \times 123)(\bmod 2347)\) M1A1
OR
\(x = – 706 + 2347n\) M1A1
solution: 1641 A1
[3 marks]
\(5(\bmod 2347) = ( – 3530 \times 123)(\bmod 2347)\) (M1)
\({\text{GS}}:z = – 3530 + k2347\) A1A1
Note: Other common possibilities include \(1164 + k2347\) and \(8205 + k2347\) .
[3 marks]
empty set (123 and 2346 both divisible by 3) A1
[1 mark]
Examiners report
The majority of candidates were successful in parts (a) and (b). In part (c), some candidates failed to understand the distinction between a particular solution and a general solution. Part (d) was a 1 mark question that defeated all but the few who noticed that the gcd of the numbers concerned was 3.
The majority of candidates were successful in parts (a) and (b). In part (c), some candidates failed to understand the distinction between a particular solution and a general solution. Part (d) was a 1 mark question that defeated all but the few who noticed that the gcd of the numbers concerned was 3.
The majority of candidates were successful in parts (a) and (b). In part (c), some candidates failed to understand the distinction between a particular solution and a general solution. Part (d) was a 1 mark question that defeated all but the few who noticed that the gcd of the numbers concerned was 3.
The majority of candidates were successful in parts (a) and (b). In part (c), some candidates failed to understand the distinction between a particular solution and a general solution. Part (d) was a 1 mark question that defeated all but the few who noticed that the gcd of the numbers concerned was 3.
Question
a.Use the result \(2003 = 6 \times 333 + 5\) and Fermat’s little theorem to show that \({2^{2003}} \equiv 4(\bmod 7)\) .[3]
b.Find \({2^{2003}}(\bmod 11)\) and \({2^{2003}}(\bmod 13)\).[3]
c.Use the Chinese remainder theorem, or otherwise, to evaluate \({2^{2003}}(\bmod 1001)\), noting that \(1001 = 7 \times 11 \times 13\).[7]
▶️Answer/Explanation
Markscheme
\({2^{2003}} = {2^5} \times {({2^6})^{333}}\) M1A1
\( \equiv 32 \times 1(\bmod 7)\) by Fermat’s little theorem A1
\( \equiv 4(\bmod 7)\) AG
[3 marks]
\(2003 = 3 + 10 \times 200\) (M1)
\({2^{2003}} = {2^3} \times {({2^{10}})^{200}}\left( { \equiv 8 \times 1(\bmod 11)} \right) \equiv 8(\bmod 11)\) A1
\({2^{2003}} = {2^{11}} \times {({2^{12}})^{166}} \equiv 7(\bmod 13)\) A1
[3 marks]
form \({M_1} = \frac{{1001}}{7} = 143;{\text{ }}{M_2} = \frac{{1001}}{{11}} = 91;{\text{ }}{M_3} = \frac{{1001}}{{13}} = 77\) M1
solve \(143{x_1} \equiv 1(\bmod 7) \Rightarrow {x_1} = 5\) M1A1
\({x_2} = 4;{\text{ }}{x_3} = 12\) A1A1
\(x = 4 \times 143 \times 5 + 8 \times 91 \times 4 + 7 \times 77 \times 12 = 12240 \equiv 228(\bmod 1001)\) M1A1
[7 marks]
Examiners report
Many candidates were able to complete part (a) and then went on to part (b). Some candidates raced through part (c). Others, who attempted part (c) using the alternative strategy of repeatedly solving linear congruencies, were sometimes successful.
Many candidates were able to complete part (a) and then went on to part (b). Some candidates raced through part (c). Others, who attempted part (c) using the alternative strategy of repeatedly solving linear congruencies, were sometimes successful.
Many candidates were able to complete part (a) and then went on to part (b). Some candidates raced through part (c). Others, who attempted part (c) using the alternative strategy of repeatedly solving linear congruencies, were sometimes successful.
Question
Consider the linear congruence \(ax \equiv b\left( {{\text{mod}}\,p} \right)\) where \(a,\,b,\,p,\,x \in {\mathbb{Z}^ + }\), \(p\) is prime and \(a\) is not a multiple of \(p\).
a.State Fermat’s little theorem.[2]
b.i.Use Fermat’s little theorem to show that \(x \equiv {a^{p – 2}}b\left( {{\text{mod}}\,p} \right)\).[3]
b.ii.Hence solve the linear congruence \(5x \equiv 7\left( {{\text{mod}}\,13} \right)\).[3]
▶️Answer/Explanation
Markscheme
EITHER
if \(p\) is prime (and \(a\) is any integer) then \({a^p} \equiv a\left( {{\text{mod}}\,p} \right)\) A1A1
Note: Award A1 for \(p\) prime and A1 for the congruence or for stating that \(p\left| {{a^p} – a} \right.\).
OR
A1A1
Note: Award A1 for \(p\) prime and A1 for the congruence or for stating that \(p\left| {{a^{p – 1}} – 1} \right.\).
Note: Condone use of equals sign provided \(\left( {{\text{mod}}\,p} \right)\) is seen.
[2 marks]
multiplying both sides of the linear congruence by \({a^{p – 2}}\) (M1)
\({a^{p – 1}}x \equiv {a^{p – 2}}b\left( {{\text{mod}}\,p} \right)\) A1
as \({a^{p – 1}} \equiv 1\left( {{\text{mod}}\,p} \right)\) R1
\(x \equiv {a^{p – 2}}b\left( {{\text{mod}}\,p} \right)\) AG
[3 marks]
\(x \equiv {5^{11}} \times 7\left( {{\text{mod}}\,13} \right)\) (M1)
\( \equiv 341796875\left( {{\text{mod}}\,13} \right)\) (A1)
Note: Accept equivalent calculation eg, using \({5^2} \equiv – 1\,{\text{mod}}\,13\).
\( \equiv 4\left( {{\text{mod}}\,13} \right)\) A1
[3 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
Let the greatest common divisor of 861 and 957 be h .
a.Using the Euclidean algorithm, find h .[4]
b.Hence find integers A and B such that 861A + 957B = h .[3]
c.Using part (b), solve \(287w \equiv 2(\bmod 319\)) , where \(w \in \mathbb{N},{\text{ }}w < 319\) .[5]
d.Find the general solution to the diophantine equation \(861x + 957y = 6\) .[6]
▶️Answer/Explanation
Markscheme
METHOD 1
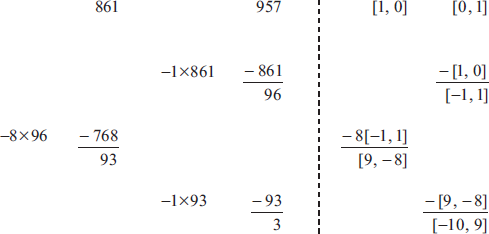
by the above working on the left (or similar) M1A1A1
Note: Award A1 for 96 and A1 for 93.
h = 3 (since 3 divides 93) A1
[4 marks]
METHOD 2
\(957 = 861 + 96\) M1A1
\(861 = 8 \times 96 + 93\) A1
\(96 = 93 + 3\)
so h = 3 (since 3 divides 93) A1
[4 marks]
METHOD 1
if method 1 was used for part (a)
by the above working on the right (or equivalent) M1
\( – 10 \times 861 + 9 \times 957 = 3\)
so A = –10 and B = 9 A1A1
[3 marks]
METHOD 2
\(3 = 96 – 93\)
\( = 96 – (861 – 8 \times 96) = 9 \times 96 – 861\) M1
\( = 9 \times (957 – 861) – 861\)
\( = – 10 \times 861 + 9 \times 957\)
so A = –10 and B = 9 A1A1
[3 marks]
from (b) \( – 10 \times 287 + 9 \times 319 = 1\) so A1
\( – 10 \times 287 \equiv 1(\bmod 319)\) A1
\(287w \equiv 2(\bmod 319) \Rightarrow – 10 \times 287w \equiv – 10 \times 2(\bmod 319)\) M1
\( \Rightarrow w \equiv – 20(\bmod 319)\) A1
so \(w = 299\) A1
[5 marks]
from (b) \( – 10 \times 861 + 9 \times 957 = 3 \Rightarrow – 20 \times 861 + 18 \times 957 = 6\) M1A1
so general solution is \(x = – 20 + 319t\) A1A1
\(y = 18 – 287t\,\,\,\,\,(t \in \mathbb{Z})\) A1A1
[6 marks]
Examiners report
The Euclidean algorithm was well applied. If it is done in the format shown in the mark scheme then the keeping track method of the linear combinations of the 2 original numbers makes part (b) easier.
Again well answered but not quite as good as (a).
Surprisingly, since it is basic bookwork, this part was answered very badly indeed. Most candidates did not realise that \( – 10\) was the number to multiply by. Sadly, of the candidates that did do it, some did not read the question carefully enough to see that a positive integer answer was required.
Again this is standard bookwork. It was answered better than part (c). There were the usual mistakes in the final answer e.g. not having the two numbers, with the parameter, co-prime.
Question
a.Convert the decimal number 51966 to base 16.[4]
b.(i) Using the Euclidean algorithm, find the greatest common divisor, d , of 901 and 612.
(ii) Find integers p and q such that 901p + 612q = d .
(iii) Find the least possible positive integers s and t such that 901s − 612t = 85.[10]
c.In each of the following cases find the solutions, if any, of the given linear congruence.
(i) \(9x \equiv 3(\bmod 18)\)
(ii) \(9x \equiv 3(\bmod 15)\)[5]
▶️Answer/Explanation
Markscheme
the relevant powers of 16 are 16, 256 and 4096
then
\(51966 = 12 \times 4096{\text{ remainder }}2814\) M1A1
\(2814 = 10 \times 256{\text{ remainder }}254\)
\(254 = 15 \times 16{\text{ remainder }}14\) A1
the hexadecimal number is CAFE A1
Note: CAFE is produced using a standard notation, accept explained alternative notations.
[4 marks]
(i) using the Euclidean Algorithm (M1)
\(901 = 612 + 289\) (A1)
\(612 = 2 \times 289 + 34\)
\(289 = 8 \times 34 + 17\)
\(\gcd (901,{\text{ }}612) = 17\) A1
(ii) working backwards (M1)
\(17 = 289 – 8 \times 34\)
\( = 289 – 8 \times (612 – 2 \times 289)\)
\( = 17 \times (901 – 612) – 8 \times 612\)
\( = 27 \times 901 – 25 \times 612\)
\({\text{so }}p = 17,{\text{ }}q = – 25\) A1A1
(iii) a particular solution is
\(s = 5p = 85,{\text{ }}t = – 5q = 125\) (A1)
the general solution is
\(s = 85 + 36\lambda ,{\text{ }}t = 125 + 53\lambda \) M1A1
by inspection the solution satisfying all conditions is
\((\lambda = – 2),{\text{ }}s = 13,{\text{ }}t = 19\) A1
[10 marks]
(i) the congruence is equivalent to \(9x = 3 + 18\lambda \) (A1)
this has no solutions as 9 does not divide the RHS R1
(ii) the congruence is equivalent to \(3x = 1 + 5\lambda ,{\text{ }}\left( {3x \equiv 1(\bmod 5)} \right)\) A1
one solution is \(x = 2\) , so the general solution is \(x = 2 + 5n\,\,\,\,\,\left( {x \equiv 2(\bmod 5)} \right)\) M1A1
[5 marks]
Examiners report
Many did not seem familiar with hexadecimal notation and often left their answer as 12101514 instead of CAFE.
The Euclidean algorithm was generally found to be easy to deal with but getting a general solution in part (iii) eluded many candidates.
Rewriting the congruence in the form \(9x = 3 + 18\lambda \) for example was not often seen but should have been the first thing thought of.
