Question
The positive integer N is expressed in base p as \({({a_n}{a_{n – 1}}…{a_1}{a_0})_p}\) .
a.Show that when p = 2 , N is even if and only if its least significant digit, \({a_0}\) , is 0.[5]
b.Show that when p = 3 , N is even if and only if the sum of its digits is even.[6]
▶️Answer/Explanation
Markscheme
\(N = {a_n} \times {2^n} + {a_{n – 1}} \times {2^{n – 1}} + … + {a_1} \times 2 + {a_0}\) M1
If \({a_0} = 0\) , then N is even because all the terms are even. R1
Now consider
\({a_0} = N – \sum\limits_{r = 1}^n {{a_r} \times {2^r}} \) M1
If N is even, then \({a_0}\) is the difference of two even numbers and is therefore even. R1
It must be zero since that is the only even digit in binary arithmetic. R1
[5 marks]
\(N = {a_n} \times {3^n} + {a_{n – 1}} \times {3^{n – 1}} + … + {a_1} \times 3 + {a_0}\)
\( = {a_n} \times ({3^n} – 1) + {a_{n – 1}} \times ({3^{n – 1}} – 1) + … + {a_1} \times (3 – 1) + {a_n} + {a_{n – 1}} + … + {a_1} + {a_0}\) M1A1
Since \({3^n}\) is odd for all \(n \in {\mathbb{Z}^ + }\) , it follows that \({3^n} – 1\) is even. R1
Therefore if the sum of the digits is even, N is the sum of even numbers and is even. R1
Now consider
\({a_n} + {a_{n – 1}} + … + {a_1} + {a_0} = N – \sum\limits_{r = 1}^n {{a_r}({3^r} – 1)} \) M1
If N is even, then the sum of the digits is the difference of even numbers and is therefore even. R1
[6 marks]
Examiners report
The response to this question was disappointing. Many candidates were successful in showing the ‘if’ parts of (a) and (b) but failed even to realise that they had to continue to prove the ‘only if’ parts.
The response to this question was disappointing. Many candidates were successful in showing the ‘if’ parts of (a) and (b) but failed even to realise that they had to continue to prove the ‘only if’ parts.
Question
a.Convert the decimal number 51966 to base 16.[4]
b.(i) Using the Euclidean algorithm, find the greatest common divisor, d , of 901 and 612.
(ii) Find integers p and q such that 901p + 612q = d .
(iii) Find the least possible positive integers s and t such that 901s − 612t = 85.[10]
c.In each of the following cases find the solutions, if any, of the given linear congruence.
(i) \(9x \equiv 3(\bmod 18)\)
(ii) \(9x \equiv 3(\bmod 15)\)[5]
▶️Answer/Explanation
Markscheme
the relevant powers of 16 are 16, 256 and 4096
then
\(51966 = 12 \times 4096{\text{ remainder }}2814\) M1A1
\(2814 = 10 \times 256{\text{ remainder }}254\)
\(254 = 15 \times 16{\text{ remainder }}14\) A1
the hexadecimal number is CAFE A1
Note: CAFE is produced using a standard notation, accept explained alternative notations.
[4 marks]
(i) using the Euclidean Algorithm (M1)
\(901 = 612 + 289\) (A1)
\(612 = 2 \times 289 + 34\)
\(289 = 8 \times 34 + 17\)
\(\gcd (901,{\text{ }}612) = 17\) A1
(ii) working backwards (M1)
\(17 = 289 – 8 \times 34\)
\( = 289 – 8 \times (612 – 2 \times 289)\)
\( = 17 \times (901 – 612) – 8 \times 612\)
\( = 27 \times 901 – 25 \times 612\)
\({\text{so }}p = 17,{\text{ }}q = – 25\) A1A1
(iii) a particular solution is
\(s = 5p = 85,{\text{ }}t = – 5q = 125\) (A1)
the general solution is
\(s = 85 + 36\lambda ,{\text{ }}t = 125 + 53\lambda \) M1A1
by inspection the solution satisfying all conditions is
\((\lambda = – 2),{\text{ }}s = 13,{\text{ }}t = 19\) A1
[10 marks]
(i) the congruence is equivalent to \(9x = 3 + 18\lambda \) (A1)
this has no solutions as 9 does not divide the RHS R1
(ii) the congruence is equivalent to \(3x = 1 + 5\lambda ,{\text{ }}\left( {3x \equiv 1(\bmod 5)} \right)\) A1
one solution is \(x = 2\) , so the general solution is \(x = 2 + 5n\,\,\,\,\,\left( {x \equiv 2(\bmod 5)} \right)\) M1A1
[5 marks]
Examiners report
Many did not seem familiar with hexadecimal notation and often left their answer as 12101514 instead of CAFE.
The Euclidean algorithm was generally found to be easy to deal with but getting a general solution in part (iii) eluded many candidates.
Rewriting the congruence in the form \(9x = 3 + 18\lambda \) for example was not often seen but should have been the first thing thought of.
Question
Show that a positive integer, written in base 10, is divisible by 9 if the sum of its digits is divisible by 9.
The representation of the positive integer N in base p is denoted by \({(N)_p}\) .
If \({({5^{{{(126)}_7}}})_7} = {({a_n}{a_{n – 1}} \ldots {a_1}{a_0})_7}\) , find \({a_0}\) .
▶️Answer/Explanation
Markscheme
consider the decimal number \(A = {a_n}{a_{n – 1}} \ldots {a_0}\) M1
\(A = {A_n} \times {10^n} + {a_{n – 1}} \times {10^{n – 1}} + \ldots + {a_1} \times 10 + {a_0}\) M1
\( = {a_n} \times ({10^n} – 1) + {a_{n – 1}} \times ({10^{n – 1}} – 1) + \ldots + {a_1} \times (10 – 1) + {a_n} + {a_{n – 1}} + \ldots + {a_0}\) M1A1
\( = {a_n} \times 99 \ldots 9(n{\text{ digits}}) + {a_{n – 1}} \times 99 \ldots 9(n – 1{\text{ digits}}) + \ldots + 9{a_1} + {a_n} + {a_{n – 1}} + \ldots + {a_0}\) A1
all the numbers of the form 99…9 are divisible by 9 (to give 11…1), R1
hence A is divisible by 9 if \(\sum\limits_{i = 0}^n {{a_i}} \) is divisible by 9 R1
Note: A method that uses the fact that \({10^t} \equiv 1(\bmod 9)\) is equally valid.
[7 marks]
by Fermat’s Little Theorem \({5^6} \equiv 1(\bmod 7)\) M1A1
\({(126)_7} = {(49 + 14 + 6)_{10}} = {(69)_{10}}\) M1A1
\({5^{{{(126)}_7}}} \equiv {5^{{{(11 \times 6 + 3)}_{10}}}} \equiv {5^{{{(3)}_{10}}}}(\bmod 7)\) M1A1
\({5^{{{(3)}_{10}}}} = {(125)_{10}} = {(17 \times 7 + 6)_{10}} \equiv 6(\bmod 7)\) M1A1
hence \({a_0} = 6\) A1
[9 marks]
Examiners report
Questions similar to (a) have been asked in the past so it was surprising to see that solutions this time were generally disappointing.
In (b), most candidates changed the base 7 number 126 to the base 10 number 69. After that the expectation was that Fermat’s little theorem would be used to complete the solution but few candidates actually did that. Many were unable to proceed any further and others used a variety of methods, for example working modulo 7,
\({5^{69}} = {({5^2})^{34}}.5 = {4^{34}}.5 = {({4^2})^{17}}.5 = {2^{17}}.5\) etc
This is of course a valid method, but somewhat laborious.
Question
The positive integer N is expressed in base 9 as \({({a_n}{a_{n – 1}} \ldots {a_0})_9}\).
(a) Show that N is divisible by 3 if the least significant digit, \({a_0}\), is divisible by 3.
(b) Show that N is divisible by 2 if the sum of its digits is even.
(c) Without using a conversion to base 10, determine whether or not \({(464860583)_9}\) is divisible by 12.
Answer/Explanation
Markscheme
(a) let \(N = {a_n}{a_{n – 1}} \ldots {a_1}{a_0} = {a_n} \times {9^n} + {a_{n – 1}} \times {9^{n – 1}} + \ldots + {a_1} \times 9 + {a_0}\) M1A1
all terms except the last are divisible by 3 and so therefore is their sum R1
it follows that N is divisible by 3 if \({a_0}\) is divisible by 3 AG
[3 marks]
(b) EITHER
consider N in the form
\(N = {a_n} \times ({9^n} – 1) + {a_{n – 1}} \times ({9^{n – 1}} – 1) + \ldots + {a_1}(9 – 1) + \sum\limits_{i = 1}^n {{a_i}} \) M1A1
all terms except the last are even so therefore is their sum R1
it follows that N is even if \(\sum\limits_{i = 0}^n {{a_i}} \) is even AG
OR
working modulo 2, \({9^k} \equiv 1(\bmod 2)\) M1A1
hence \(N = {a_n}{a_{n – 1}} \ldots {a_1}{a_0} = {a_n} \times {9^n} + {a_{n – 1}} \times {9^{n – 1}} + \ldots + {a_1} \times 9 + {a_0} = \sum\limits_{i = 0}^n {{a_i}(\bmod 2)} \) R1
it follows that N is even if \(\sum\limits_{i = 0}^n {{a_i}} \) is even AG
[3 marks]
(c) the number is divisible by 3 because the least significant digit is 3 R1
it is divisible by 2 because the sum of the digits is 44 which is even R1
dividing the number by 2 gives \({(232430286)_9}\) M1A1
which is even because the sum of the digits is 30 which is even R1
N is therefore divisible by a further 2 and is therefore divisible by 12 R1
Note: Accept alternative valid solutions.
[6 marks]
Total [12 marks]
Examiners report
Parts (a) and (b) were generally well answered. Part (c), however, caused problems for many candidates with some candidates even believing that showing divisibility by 2 and 3 was sufficient to prove divisibility by 12. Some candidates stated that the fact that the sum of the digits was 44 (which itself is divisible by 4) indicated divisibility by 4 but this was only accepted if the candidates extended their proof in (b) to cover divisibility by 4.
Question
(a) Write down Fermat’s little theorem.
(b) In base 5 the representation of a natural number X is \({\left( {k00013(5 – k)} \right)_5}\).
This means that \(X = k \times {5^6} + 1 \times {5^2} + 3 \times 5 + (5 – k)\).
In base 7 the representation of X is \({({a_n}{a_{n – 1}} \ldots {a_2}{a_1}{a_0})_7}\).
Find \({a_0}\).
(c) Given that k = 2, find X in base 7.
▶️Answer/Explanation
Markscheme
(a) EITHER
if p is a prime \({a^p} \equiv a(\bmod p)\) A1A1
OR
if p is a prime and \(a\) \(0(\bmod p)\) then \({a^{p – 1}} \equiv 1(\bmod p)\) A1A1
Note: Award A1 for p being prime and A1 for the congruence.
[2 marks]
(b) \({a_0} \equiv X(\bmod 7)\) M1
\(X = k \times {5^6} + 25 + 15 + 5 – k\)
by Fermat \({5^6} \equiv 1(\bmod 7)\) R1
\(X = k + 45 – k(\bmod 7)\) (M1)
\(X = 3(\bmod 7)\) A1
\({a_0} = 3\) A1
[5 marks]
(c) \(X = 2 \times {5^6} + 25 + 15 + 3 = 31\,293\) A1
EITHER
\(X – {7^5} = 14\,486\) (M1)
\(X – {7^5} – 6 \times {7^4} = 80\)
\(X – {7^5} – 6 \times {7^4} – {7^2} = 31\)
\(X – {7^5} – 6 \times {7^4} – {7^2} – 4 \times 7 = 3\)
\(X = {7^5} + 6 \times {7^4} + {7^2} + 4 \times 7 + 3\) (A1)
\(X = {(160\,143)_7}\) A1
OR
\(31\,293 = 7 \times 4470 + 3\) (M1)
\(4470 = 7 \times 638 + 4\)
\(638 = 7 \times 91 + 1\)
\(91 = 7 \times 13 + 0\)
\(13 = 7 \times 1 + 6\) (A1)
\(X = {(160\,143)_7}\) A1
[4 marks]
Total [11 marks]
Examiners report
Fermat’s little theorem was reasonably well known. Not all candidates took the hint to use this in the next part and this part was not done well. Part (c) could and was done even if part (b) was not.
Question
Given that a , \(b \in \mathbb{N}\) and \(c \in {\mathbb{Z}^ + }\), show that if \(a \equiv 1(\bmod c)\) , then \(ab \equiv b(\bmod c)\) .
Using mathematical induction, show that \({9^n} \equiv 1(\bmod 4)\) , for \(n \in \mathbb{N}\) .
The positive integer M is expressed in base 9. Show that M is divisible by 4 if the sum of its digits is divisible by 4.
▶️Answer/Explanation
Markscheme
\(a = \lambda c + 1\) M1
so \(ab = \lambda bc + b \Rightarrow ab \equiv b(\bmod c)\) A1AG
[2 marks]
the result is true for n = 0 since \({9^0} = 1 \equiv 1(\bmod 4)\) A1
assume the result is true for n = k , i.e. \({9^k} \equiv 1(\bmod 4)\) M1
consider \({9^{k + 1}} = 9 \times {9^k}\) M1
\( \equiv 9 \times 1(\bmod 4)\) or \(1 \times {9^k}(\bmod 4)\) A1
\( \equiv 1(\bmod 4)\) A1
so true for \(n = k \Rightarrow \) true for n = k + 1 and since true for n = 0 result follows by induction R1
Note: Do not award the final R1 unless both M1 marks have been awarded.
Note: Award the final R1 if candidates state n = 1 rather than n = 0
[6 marks]
let \(M = {({a_n}{a_{n – 1}}…{a_0})_9}\) (M1)
\( = {a_n} \times {9^n} + {a_{n – 1}} \times {9^{n – 1}} + … + {a_0} \times {9^0}\) A1
EITHER
\( \equiv {a_n}(\bmod 4) + {a_{n – 1}}(\bmod 4) + … + {a_0}(\bmod 4)\) A1
\( \equiv \sum {{a_i}(\bmod 4)} \) A1
so M is divisible by 4 if \(\sum {{a_i}} \) is divisible by 4 AG
OR
\( = {a_n}({9^n} – 1) + {a_{n – 1}}({9^{n – 1}} – 1) + … + {a_1}({9^1} – 1)\)
\( + {a_n} + {a_{n – 1}} + … + {a_1} + {a_0}\) A1
Since \({9^n} \equiv 1(\bmod 4)\) , it follows that \({9^n} – 1\) is divisible by 4, R1
so M is divisible by 4 if \(\sum {{a_i}} \) is divisible by 4 AG
[4 marks]
Examiners report
Part (a) was generally well answered. In (b), many candidates tested the result for n = 1 instead of n = 0. It has been suggested that the reason for this was a misunderstanding of the symbol N with some candidates believing it to denote the positive integers. It is important for candidates to be familiar with IB notation in which N denotes the positive integers and zero. In some scripts the presentation of the proof by induction was poor.
Part (a) was generally well answered. In (b), many candidates tested the result for n = 1 instead of n = 0. It has been suggested that the reason for this was a misunderstanding of the symbol N with some candidates believing it to denote the positive integers. It is important for candidates to be familiar with IB notation in which N denotes the positive integers and zero. In some scripts the presentation of the proof by induction was poor.
Part (a) was generally well answered. In (b), many candidates tested the result for n = 1 instead of n = 0. It has been suggested that the reason for this was a misunderstanding of the symbol N with some candidates believing it to denote the positive integers. It is important for candidates to be familiar with IB notation in which N denotes the positive integers and zero. In some scripts the presentation of the proof by induction was poor.
Question
Consider an integer \(a\) with \((n + 1)\) digits written as \(a = {10^n}{a_n} + {10^{n – 1}}{a_{n – 1}} + \ldots + 10{a_1} + {a_0}\), where \(0 \leqslant {a_i} \leqslant 9\) for \(0 \leqslant i \leqslant n\), and \({a_n} \ne 0\).
(a) Show that \(a \equiv ({a_n} + {a_{n – 1}} + \ldots + {a_0}) ({\text{mod9}})\).
(b) Hence find all pairs of values of the single digits \(x\) and \(y\) such that the number \(a = 476x212y\) is a multiple of \(45\).
(c) (i) If \(b = 34\,390\) in base 10, show that \(b\) is \(52\,151\) written in base 9.
(ii) Hence find \({b^2}\) in base 9, by performing all the calculations without changing base.
▶️Answer/Explanation
Markscheme
(a) \(10 \equiv 1(\bmod 9) \Rightarrow {10^i} \equiv 1({\text{mod9}}),{\text{ }}i = 1,{\text{ }} … ,{\text{ }}n\) M1A1
\( \Rightarrow {10^i}{a_i} \equiv {a_i}({\text{mod9}}),{\text{ }}i = 1,{\text{ }}n\) M1
Note: Allow \(i = 0\) but do not penalize its omission.
\( \Rightarrow ({10^n}{a_n} + {10^{n – 1}}{a_{n – 1}} + \ldots + {a_0}) \equiv ({a_n} + {a_{n – 1}} + \ldots + {a_0})({\text{mod9}})\) AG
[3 marks]
(b) \(4 + 7 + 6 + x + 2 + 1 + 2 + y = 9k,{\text{ }}k \in \mathbb{Z}\) (M1)
\( \Rightarrow (22 + x + y) \equiv 0(\bmod 9),{\text{ }} \Rightarrow (x + y) \equiv 5({\text{mod9}})\)
\( \Rightarrow x + y = 5\) or \(14\) A1
if \(5\) divides \(a\), then \(y = 0\) or \(5\) M1
so \(y = 0 \Rightarrow x = 5,{\text{ }}\left( {ie{\text{ }}(x,{\text{ }}y) = (5,{\text{ }}0)} \right)\) A1
\(y = 5 \Rightarrow x = 0\) or \(x = 9,{\text{ }}\left( {ie{\text{ }}(x,{\text{ }}y) = (0,{\text{ }}5){\text{ or }}(x,{\text{ }}y) = (9,{\text{ }}5)} \right)\) A1A1
[6 marks]
(c) (i)  (M1)A1
(M1)A1
\(b = {(52\,151)_9}\) AG
(ii) 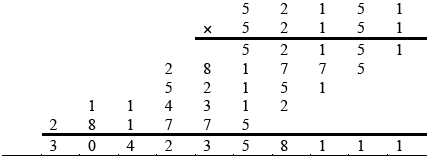 M1A3
M1A3
Note: M1 for attempt, A1 for two correct lines of multiplication, A2 for two correct lines of multiplication and a correct addition, A3 for all correct.
[6 marks]
Examiners report
Surprisingly few good answers. Part (a) had a number of correct solutions, but there were also many that seemed to be a memorised solution, not properly expressed – and consequently wrong. In part (b) many failed to understand the question, not registering that x and y were digits rather than numbers. Part (c)(i) was generally well answered, although there were a number of longer methods applied, and few managed to do (c)(ii).

