Question
Let \(f(x) = \frac{{3x}}{2} + 1\) , \(g(x) = 4\cos \left( {\frac{x}{3}} \right) – 1\) . Let \(h(x) = (g \circ f)(x)\) .
Find an expression for \(h(x)\) .
Write down the period of \(h\) .
Write down the range of \(h\) .
Answer/Explanation
Markscheme
attempt to form any composition (even if order is reversed) (M1)
correct composition \(h(x) = g\left( {\frac{{3x}}{2} + 1} \right)\) (A1)
\(h(x) = 4\cos \left( {\frac{{\frac{{3x}}{2} + 1}}{3}} \right) – 1\) \(\left( {4\cos \left( {\frac{1}{2}x + \frac{1}{3}} \right) – 1,4\cos \left( {\frac{{3x + 2}}{6}} \right) – 1} \right)\) A1 N3
[3 marks]
period is \(4\pi (12.6)\) A1 N1
[1 mark]
range is \( – 5 \le h(x) \le 3\) \(\left( {\left[ { – 5,3} \right]} \right)\) A1A1 N2
[2 marks]
Question
Let \(f(x) = 3x\) , \(g(x) = 2x – 5\) and \(h(x) = (f \circ g)(x)\) .
Find \(h(x)\) .
Find \({h^{ – 1}}(x)\) .
Answer/Explanation
Markscheme
attempt to form composite (M1)
e.g. \(f(2x – 5)\)
\(h(x) = 6x – 15\) A1 N2
[2 marks]
interchanging x and y (M1)
evidence of correct manipulation (A1)
e.g. \(y + 15 = 6x\) , \(\frac{x}{6} = y – \frac{5}{2}\)
\({h^{ – 1}}(x) = \frac{{x + 15}}{6}\) A1 N3
[3 marks]
Question
Let \(f(x) = 2x + 4\) and \(g(x) = 7{x^2}\) .
Find \({f^{ – 1}}(x)\) .
Find \((f \circ g)(x)\) .
Find \((f \circ g)(3.5)\) .
Answer/Explanation
Markscheme
interchanging x and y (may be seen at any time) (M1)
evidence of correct manipulation (A1)
e.g. \(x = 2y + 4\)
\({f^{ – 1}}(x) = \frac{{x – 4}}{2}\) (accept \(y = \frac{{x – 4}}{2},\frac{{x – 4}}{2}\) ) A1 N2
[3 marks]
attempt to form composite (in any order) (M1)
e.g. \(f(7{x^2}){\text{, }}2(7{x^2}) + 4{\text{, }}7{(2x + 4)^2}\)
\((f \circ g)(x) = 14{x^2} + 4\) A1 N2
correct substitution (A1)
e.g. \(7 \times {3.5^2}\) , \(14{(3.5)^2} + 4\)
\((f \circ g)(3.5) = 175.5\) (accept 176) A1 N2
[2 marks]
Question
Let \(f(x) = 2x + 3\) and \(g(x) = {x^3}\).
Find \((f \circ g)(x)\).
Solve the equation \((f \circ g)(x) = 0\).
Answer/Explanation
Markscheme
attempt to form composite (in any order) (M1)
eg\(\;\;\;f({x^3}),{\text{ }}{(2x + 3)^3}\)
\((f \circ g)(x) = 2{x^3} + 3\) A1 N2
[2 marks]
evidence of appropriate approach (M1)
eg\(\;\;\;2{x^3} = – 3\), sketch
correct working (A1)
eg\(\;\;\;{x^3} = \frac{{ – 3}}{2}\), sketch
\( – 1.14471\)
\(x = \sqrt[3]{{\frac{{ – 3}}{2}}}\;\;\;{\text{(exact), }} – 1.14{\text{ }}[ – 1.15,{\text{ }} – 1.14]\) A1 N3
[3 marks]
Total [5 marks]
Question
Consider a function \(f\), for \(0 \le x \le 10\). The following diagram shows the graph of \(f’\), the derivative of \(f\).
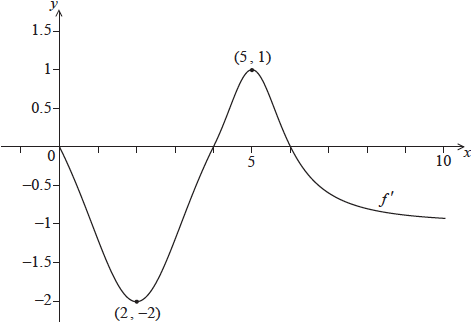
The graph of \(f’\) passes through \((2,{\text{ }} – 2)\) and \((5,{\text{ }}1)\), and has \(x\)-intercepts at \(0\), \(4\) and \(6\).
The graph of \(f\) has a local maximum point when \(x = p\). State the value of \(p\), and justify your answer.
Write down \(f'(2)\).
Let \(g(x) = \ln \left( {f(x)} \right)\) and \(f(2) = 3\).
Find \(g'(2)\).
Verify that \(\ln 3 + \int_2^a {g'(x){\text{d}}x = g(a)} \), where \(0 \le a \le 10\).
The following diagram shows the graph of \(g’\), the derivative of \(g\).
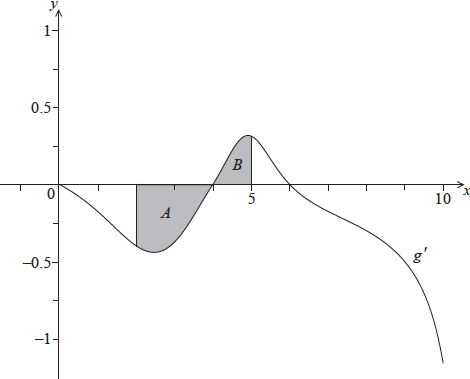
The shaded region \(A\) is enclosed by the curve, the \(x\)-axis and the line \(x = 2\), and has area \({\text{0.66 unit}}{{\text{s}}^{\text{2}}}\).
The shaded region \(B\) is enclosed by the curve, the \(x\)-axis and the line \(x = 5\), and has area \({\text{0.21 unit}}{{\text{s}}^{\text{2}}}\).
Find \(g(5)\).
Answer/Explanation
Markscheme
\(p = 6\) A1 N1
recognizing that turning points occur when \(f'(x) = 0\) R1 N1
eg\(\;\;\;\)correct sign diagram
\(f’\) changes from positive to negative at \(x = 6\) R1 N1
[3 marks]
\(f'(2) = – 2\) A1 N1
[1 mark]
attempt to apply chain rule (M1)
eg\(\;\;\;\ln (x)’ \times f'(x)\)
correct expression for \(g'(x)\) (A1)
eg\(\;\;\;g'(x) = \frac{1}{{f(x)}} \times f'(x)\)
substituting \(x = 2\) into their \(g’\) (M1)
eg\(\;\;\;\frac{{f'(2)}}{{f(2)}}\)
\( – 0.666667\)
\(g'(2) = – \frac{2}{3}{\text{ (exact), }} – 0.667\) A1 N3
[4 marks]
evidence of integrating \(g'(x)\) (M1)
eg\(\;\;\;g(x)|_2^a,{\text{ }}g(x)|_a^2\)
applying the fundamental theorem of calculus (seen anywhere) R1
eg\(\;\;\;\int_2^a {g'(x) = g(a) – g(2)} \)
correct substitution into integral (A1)
eg\(\;\;\;\ln 3 + g(a) – g(2),{\text{ }}\ln 3 + g(a) – \ln \left( {f(2)} \right)\)
\(\ln 3 + g(a) – \ln 3\) A1
\(\ln 3 + \int_2^a {g'(x) = g(a)} \) AG N0
[4 marks]
METHOD 1
substituting \(a = 5\) into the formula for \(g(a)\) (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x,{\text{ }}g(5) = \ln 3 + \int_2^5 {g'(x){\text{d}}x\;\;\;} } \left( {{\text{do not accept only }}g(5)} \right)\)
attempt to substitute areas (M1)
eg\(\;\;\;\ln 3 + 0.66 – 0.21,{\text{ }}\ln 3 + 0.66 + 0.21\)
correct working
eg\(\;\;\;g(5) = \ln 3 + ( – 0.66 + 0.21)\) (A1)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 2
attempt to set up an equation for one shaded region (M1)
eg\(\;\;\;\int_4^5 {g'(x){\text{d}}x = 0.21,{\text{ }}\int_2^4 {g'(x){\text{d}}x = – 0.66,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } } \)
two correct equations (A1)
eg\(\;\;\;g(5) – g(4) = 0.21,{\text{ }}g(2) – g(4) = 0.66\)
combining equations to eliminate \(g(4)\) (M1)
eg\(\;\;\;g(5) – [\ln 3 – 0.66] = 0.21\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 3
attempt to set up a definite integral (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x = – 0.66 + 0.21,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } \)
correct working (A1)
eg\(\;\;\;g(5) – g(2) = – 0.45\)
correct substitution (A1)
eg\(\;\;\;g(5) – \ln 3 = – 0.45\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
[4 marks]
Total [16 marks]
Question
Let \(f(x) = {x^2} + 2x + 1\) and \(g(x) = x – 5\), for \(x \in \mathbb{R}\).
Find \(f(8)\).
Find \((g \circ f)(x)\).
Solve \((g \circ f)(x) = 0\).
Answer/Explanation
Markscheme
attempt to substitute \(x = 8\) (M1)
eg\(\,\,\,\,\,\)\({8^2} + 2 \times 8 + 1\)
\(f(8) = 81\) A1 N2
[2 marks]
attempt to form composition (in any order) (M1)
eg\(\,\,\,\,\,\)\(f(x – 5),{\text{ }}g\left( {f(x)} \right),{\text{ }}\left( {{x^2} + 2x + 1} \right) – 5\)
\((g \circ f)(x) = {x^2} + 2x – 4\) A1 N2
[2 marks]
valid approach (M1)
eg \(x = \frac{{ – 2 \pm \sqrt {20} }}{2}\), 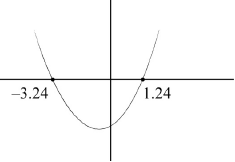
\(1.23606,{\text{ }} – 3.23606\)
\(x = 1.24,{\text{ }}x = – 3.24\) A1A1 N3
[3 marks]
Question
Let \(f(x) = {x^2} – 1\) and \(g(x) = {x^2} – 2\), for \(x \in \mathbb{R}\).
Show that \((f \circ g)(x) = {x^4} – 4{x^2} + 3\).
On the following grid, sketch the graph of \((f \circ g)(x)\), for \(0 \leqslant x \leqslant 2.25\).
The equation \((f \circ g)(x) = k\) has exactly two solutions, for \(0 \leqslant x \leqslant 2.25\). Find the possible values of \(k\).
Answer/Explanation
Markscheme
attempt to form composite in either order (M1)
eg\(\,\,\,\,\,\)\(f({x^2} – 2),{\text{ }}{({x^2} – 1)^2} – 2\)
\(({x^4} – 4{x^2} + 4) – 1\) A1
\((f \circ g)(x) = {x^4} – 4{x^2} + 3\) AG N0
[2 marks]
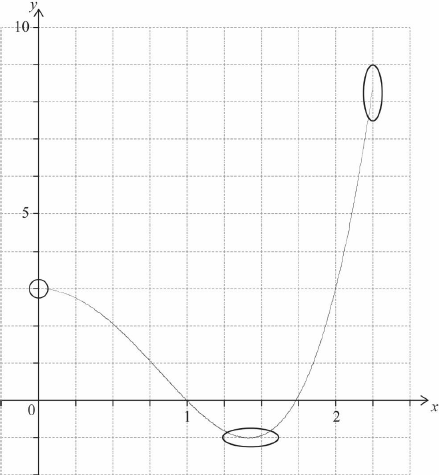 A1
A1
A1A1 N3
Note: Award A1 for approximately correct shape which changes from concave down to concave up. Only if this A1 is awarded, award the following:
A1 for left hand endpoint in circle and right hand endpoint in oval,
A1 for minimum in oval.
[3 marks]
evidence of identifying max/min as relevant points (M1)
eg\(\,\,\,\,\,\)\(x = 0,{\text{ }}1.41421,{\text{ }}y = – 1,{\text{ }}3\)
correct interval (inclusion/exclusion of endpoints must be correct) A2 N3
eg\(\,\,\,\,\,\)\( – 1 < k \leqslant 3,{\text{ }}\left] { – 1,{\text{ 3}}} \right],{\text{ }}( – 1,{\text{ }}3]\)
[3 marks]

