Question
Let f be the function given by \(f(x) = {{\rm{e}}^{0.5x}}\) , \(0 \le x \le 3.5\) . The diagram shows the graph of f .
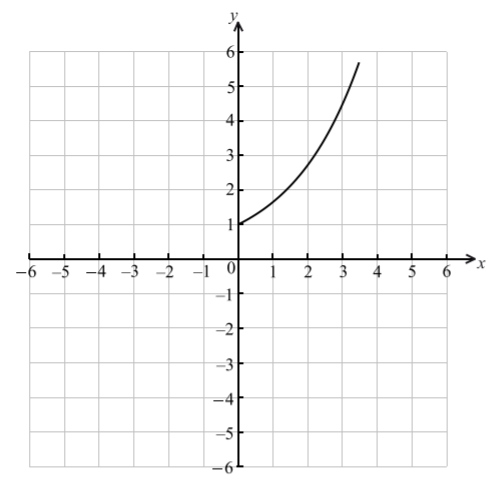
On the same diagram, sketch the graph of \({f^{ – 1}}\) .
Write down the range of \({f^{ – 1}}\) .
Find \({f^{ – 1}}(x)\) .
Answer/Explanation
Markscheme
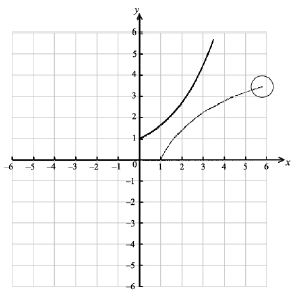
A1A1A1 N3
Note: Award A1 for approximately correct (reflected) shape, A1 for right end point in circle, A1 for through \((1{\text{, }}0)\) .
\(0 \le y \le 3.5\) A1 N1
[1 mark]
interchanging x and y (seen anywhere) M1
e.g. \(x = {e^{0.5y}}\)
evidence of changing to log form A1
e.g. \(\ln x = 0.5y\) , \(\ln x = \ln {{\rm{e}}^{0.5y}}\) (any base), \(\ln x = 0.5y\ln {\rm{e}}\) (any base)
\({f^{ – 1}}(x) = 2\ln x\) A1 N1
[3 marks]
Question
Let \(f(x) = {{\rm{e}}^{x + 3}}\) .
(i) Show that \({f^{ – 1}}(x) = \ln x – 3\) .
(ii) Write down the domain of \({f^{ – 1}}\) .
Solve the equation \({f^{ – 1}}(x) = \ln \frac{1}{x}\) .
Answer/Explanation
Markscheme
(i) interchanging x and y (seen anywhere) M1
e.g. \(x = {{\rm{e}}^{y + 3}}\)
correct manipulation A1
e.g. \(\ln x = y + 3\) , \(\ln y = x + 3\)
\({f^{ – 1}}(x) = \ln x – 3\) AG N0
(ii) \(x > 0\) A1 N1
[3 marks]
collecting like terms; using laws of logs (A1)(A1)
e.g. \(\ln x – \ln \left( {\frac{1}{x}} \right) = 3\) , \(\ln x + \ln x = 3\) , \(\ln \left( {\frac{x}{{\frac{1}{x}}}} \right) = 3\) , \(\ln {x^2} = 3\)
simplify (A1)
e.g. \(\ln x = \frac{3}{2}\) , \({x^2} = {{\rm{e}}^3}\)
\(x = {{\rm{e}}^{\frac{3}{2}}}\left( { = \sqrt {{{\rm{e}}^3}} } \right)\) A1 N2
[4 marks]
Examiners report
Many candidates interchanged the \(x\) and \(y\) to find the inverse function, but very few could write down the correct domain of the inverse, often giving \(x \ge 0\) , \(x > 3\) and “all real numbers” as responses.
Where students attempted to solve the equation in (b), most treated \(\ln x – 3\) as \(\ln (x – 3)\) and created an incorrect equation from the outset. The few who applied laws of logarithms often carried the algebra through to completion.
Question
Let \(f(x) = lo{g_3}\sqrt x \) , for \(x > 0\) .
Show that \({f^{ – 1}}(x) = {3^{2x}}\) .
Write down the range of \({f^{ – 1}}\) .
Let \(g(x) = {\log _3}x\) , for \(x > 0\) .
Find the value of \(({f^{ – 1}} \circ g)(2)\) , giving your answer as an integer.
Answer/Explanation
Markscheme
interchanging x and y (seen anywhere) (M1)
e.g. \(x = \log \sqrt y \) (accept any base)
evidence of correct manipulation A1
e.g. \(3^x = \sqrt y \) , \({3^y} = {x^{\frac{1}{2}}}\) , \(x = \frac{1}{2}{\log _3}y\) , \(2y = {\log _3}x\)
\({f^{ – 1}}(x) = {3^{2x}}\) AG N0
[2 marks]
\(y > 0\) , \({f^{ – 1}}(x) > 0\) A1 N1
[1 mark]
METHOD 1
finding \(g(2) = lo{g_3}2\) (seen anywhere) A1
attempt to substitute (M1)
e.g. \(({f^{ – 1}} \circ g)(2) = {3^{2\log {_3}2}}\)
evidence of using log or index rule (A1)
e.g. \(({f^{ – 1}} \circ g)(2) = {3^{\log {_3}4}}\) , \({3^{{{\log }_3}2^2}}\)
\(({f^{ – 1}} \circ g)(2) = 4\) A1 N1
METHOD 2
attempt to form composite (in any order) (M1)
e.g. \(({f^{ – 1}} \circ g)(x) = {3^{2{{\log }_3}x}}\)
evidence of using log or index rule (A1)
e.g. \(({f^{ – 1}} \circ g)(x) = {3^{{{\log }_3}{x^2}}}\) , \({3^{{{\log }_3}{x^{}}}}^2\)
\(({f^{ – 1}} \circ g)(x) = {x^2}\) A1
\(({f^{ – 1}} \circ g)(2) = 4\) A1 N1
[4 marks]
Question
Let \(f(x) = \sqrt {x – 5} \) , for \(x \ge 5\) .
Find \({f^{ – 1}}(2)\) .
Let \(g\) be a function such that \({g^{ – 1}}\) exists for all real numbers. Given that \(g(30) = 3\) , find \((f \circ {g^{ – 1}})(3)\) .
Answer/Explanation
Markscheme
METHOD 1
attempt to set up equation (M1)
eg \(2 = \sqrt {y – 5} \) , \(2 = \sqrt {x – 5} \)
correct working (A1)
eg \(4 = y – 5\) , \(x = {2^2} + 5\)
\({f^{ – 1}}(2) = 9\) A1 N2
METHOD 2
interchanging \(x\) and \(y\) (seen anywhere) (M1)
eg \(x = \sqrt {y – 5} \)
correct working (A1)
eg \({x^2} = y – 5\) , \(y = {x^2} + 5\)
\({f^{ – 1}}(2) = 9\) A1 N2
[3 marks]
recognizing \({g^{ – 1}}(3) = 30\) (M1)
eg \(f(30)\)
correct working (A1)
eg \((f \circ {g^{ – 1}})(3) = \sqrt {30 – 5} \) , \(\sqrt {25} \)
\((f \circ {g^{ – 1}})(3) = 5\) A1 N2
Note: Award A0 for multiple values, eg \( \pm 5\) .
[3 marks]
Question
Consider \(f(x) = \ln ({x^4} + 1)\) .
The second derivative is given by \(f”(x) = \frac{{4{x^2}(3 – {x^4})}}{{{{({x^4} + 1)}^2}}}\) .
The equation \(f”(x) = 0\) has only three solutions, when \(x = 0\) , \( \pm \sqrt[4]{3}\) \(( \pm 1.316 \ldots )\) .
Find the value of \(f(0)\) .
Find the set of values of \(x\) for which \(f\) is increasing.
(i) Find \(f”(1)\) .
(ii) Hence, show that there is no point of inflexion on the graph of \(f\) at \(x = 0\) .
There is a point of inflexion on the graph of \(f\) at \(x = \sqrt[4]{3}\) \((x = 1.316 \ldots )\) .
Sketch the graph of \(f\) , for \(x \ge 0\) .
Answer/Explanation
Markscheme
substitute \(0\) into \(f\) (M1)
eg \(\ln (0 + 1)\) , \(\ln 1\)
\(f(0) = 0\) A1 N2
[2 marks]
\(f'(x) = \frac{1}{{{x^4} + 1}} \times 4{x^3}\) (seen anywhere) A1A1
Note: Award A1 for \(\frac{1}{{{x^4} + 1}}\) and A1 for \(4{x^3}\) .
recognizing \(f\) increasing where \(f'(x) > 0\) (seen anywhere) R1
eg \(f'(x) > 0\) , diagram of signs
attempt to solve \(f'(x) > 0\) (M1)
eg \(4{x^3} = 0\) , \({x^3} > 0\)
\(f\) increasing for \(x > 0\) (accept \(x \ge 0\) ) A1 N1
[5 marks]
(i) substituting \(x = 1\) into \(f”\) (A1)
eg \(\frac{{4(3 – 1)}}{{{{(1 + 1)}^2}}}\) , \(\frac{{4 \times 2}}{4}\)
\(f”(1) = 2\) A1 N2
(ii) valid interpretation of point of inflexion (seen anywhere) R1
eg no change of sign in \(f”(x)\) , no change in concavity,
\(f’\) increasing both sides of zero
attempt to find \(f”(x)\) for \(x < 0\) (M1)
eg \(f”( – 1)\) , \(\frac{{4{{( – 1)}^2}(3 – {{( – 1)}^4})}}{{{{({{( – 1)}^4} + 1)}^2}}}\) , diagram of signs
correct working leading to positive value A1
eg \(f”( – 1) = 2\) , discussing signs of numerator and denominator
there is no point of inflexion at \(x = 0\) AG N0
[5 marks]
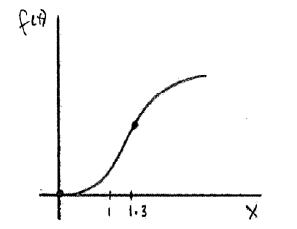
A1A1A1 N3
Notes: Award A1 for shape concave up left of POI and concave down right of POI.
Only if this A1 is awarded, then award the following:
A1 for curve through (\(0\), \(0\)) , A1 for increasing throughout.
Sketch need not be drawn to scale. Only essential features need to be clear.
[3 marks]
Question
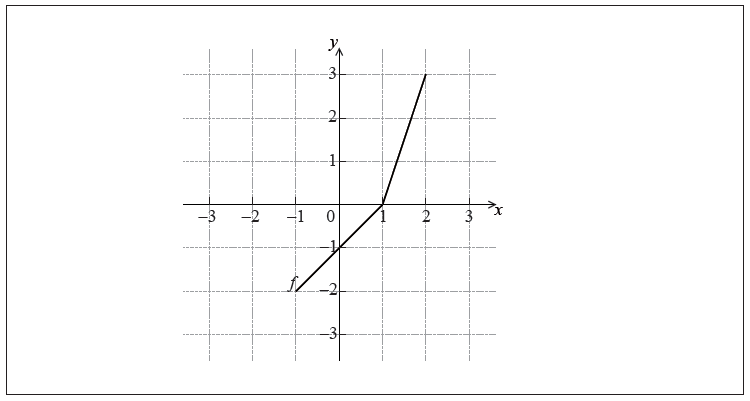
The diagram below shows the graph of a function \(f\) , for \( – 1 \le x \le 2\) .
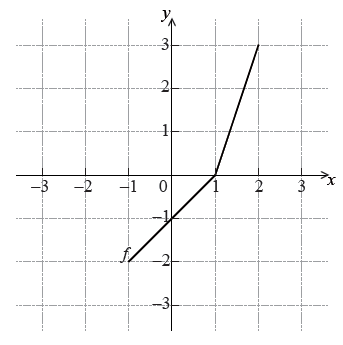
Write down the value of \(f(2)\).
Write down the value of \({f^{ – 1}}( – 1)\) .
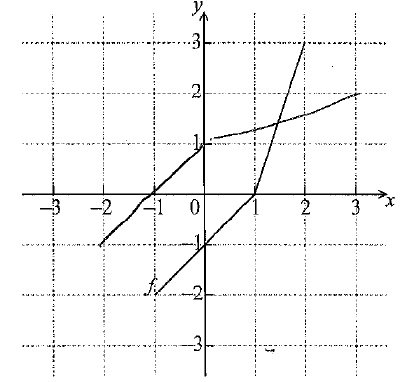
Sketch the graph of \({f^{ – 1}}\) on the grid below.
Answer/Explanation
Markscheme
\(f(2) = 3\) A1 N1
[1 mark]
\({f^{ – 1}}( – 1) = 0\) A2 N2
[2 marks]
EITHER
attempt to draw \(y = x\) on grid (M1)
OR
attempt to reverse x and y coordinates (M1)
eg writing or plotting at least two of the points
\(( – 2, – 1)\) , \(( – 1,0)\) , \((0,1)\) , \((3,2)\)
THEN
correct graph A2 N3
[3 marks]
Question
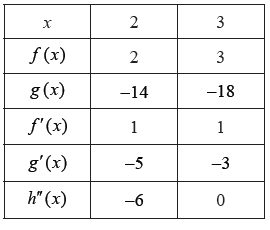
Consider the functions \(f(x)\) , \(g(x)\) and \(h(x)\) . The following table gives some values associated with these functions.
The following diagram shows parts of the graphs of \(h\) and \(h”\) .
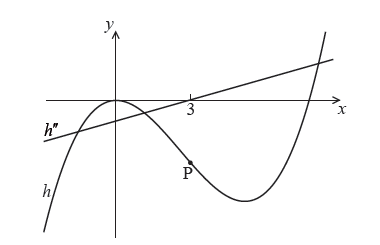
There is a point of inflexion on the graph of \(h\) at P, when \(x = 3\) .
Given that \(h(x) = f(x) \times g(x)\) ,
Write down the value of \(g(3)\) , of \(f'(3)\) , and of \(h”(2)\) .
Explain why P is a point of inflexion.
find the \(y\)-coordinate of P.
find the equation of the normal to the graph of \(h\) at P.
Answer/Explanation
Markscheme
\(g(3) = – 18\) , \(f'(3) = 1\) , \(h”(2) = – 6\) A1A1A1 N3
[3 marks]
\(h”(3) = 0\) (A1)
valid reasoning R1
eg \({h”}\) changes sign at \(x = 3\) , change in concavity of \(h\) at \(x = 3\)
so P is a point of inflexion AG N0
[2 marks]
writing \(h(3)\) as a product of \(f(3)\) and \(g(3)\) A1
eg \(f(3) \times g(3)\) , \(3 \times ( – 18)\)
\(h(3) = – 54\) A1 N1
[2 marks]
recognizing need to find derivative of \(h\) (R1)
eg \({h’}\) , \(h'(3)\)
attempt to use the product rule (do not accept \(h’ = f’ \times g’\) ) (M1)
eg \(h’ = fg’ + gf’\) , \(h'(3) = f(3) \times g'(3) + g(3) \times f'(3)\)
correct substitution (A1)
eg \(h'(3) = 3( – 3) + ( – 18) \times 1\)
\(h'(3) = – 27\) A1
attempt to find the gradient of the normal (M1)
eg \( – \frac{1}{m}\) , \( – \frac{1}{{27}}x\)
attempt to substitute their coordinates and their normal gradient into the equation of a line (M1)
eg \( – 54 = \frac{1}{{27}}(3) + b\) , \(0 = \frac{1}{{27}}(3) + b\) , \(y + 54 = 27(x – 3)\) , \(y – 54 = \frac{1}{{27}}(x + 3)\)
correct equation in any form A1 N4
eg \(y + 54 = \frac{1}{{27}}(x – 3)\) , \(y = \frac{1}{{27}}x – 54\frac{1}{9}\)
[7 marks]
Question
Let \(f(x) = 3x – 2\) and \(g(x) = \frac{5}{{3x}}\), for \(x \ne 0\).
Let \(h(x) = \frac{5}{{x + 2}}\), for \(x \geqslant 0\). The graph of h has a horizontal asymptote at \(y = 0\).
Find \({f^{ – 1}}(x)\).
Show that \(\left( {g \circ {f^{ – 1}}} \right)(x) = \frac{5}{{x + 2}}\).
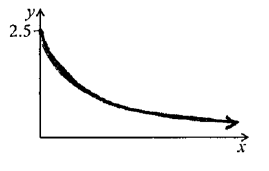
Find the \(y\)-intercept of the graph of \(h\).
Hence, sketch the graph of \(h\).
For the graph of \({h^{ – 1}}\), write down the \(x\)-intercept;
For the graph of \({h^{ – 1}}\), write down the equation of the vertical asymptote.
Given that \({h^{ – 1}}(a) = 3\), find the value of \(a\).
Answer/Explanation
Markscheme
interchanging \(x\) and \(y\) (M1)
eg \(x = 3y – 2\)
\({f^{ – 1}}(x) = \frac{{x + 2}}{3}{\text{ }}\left( {{\text{accept }}y = \frac{{x + 2}}{3},{\text{ }}\frac{{x + 2}}{3}} \right)\) A1 N2
[2 marks]
attempt to form composite (in any order) (M1)
eg \(g\left( {\frac{{x + 2}}{3}} \right),{\text{ }}\frac{{\frac{5}{{3x}} + 2}}{3}\)
correct substitution A1
eg \(\frac{5}{{3\left( {\frac{{x + 2}}{3}} \right)}}\)
\(\left( {g \circ {f^{ – 1}}} \right)(x) = \frac{5}{{x + 2}}\) AG N0
[2 marks]
valid approach (M1)
eg \(h(0),{\text{ }}\frac{5}{{0 + 2}}\)
\(y = \frac{5}{2}{\text{ }}\left( {{\text{accept (0, 2.5)}}} \right)\) A1 N2
[2 marks]
A1A2 N3
Notes: Award A1 for approximately correct shape (reciprocal, decreasing, concave up).
Only if this A1 is awarded, award A2 for all the following approximately correct features: y-intercept at \((0, 2.5)\), asymptotic to x-axis, correct domain \(x \geqslant 0\).
If only two of these features are correct, award A1.
[3 marks]
\(x = \frac{5}{2}{\text{ }}\left( {{\text{accept (2.5, 0)}}} \right)\) A1 N1
[1 mark]
\(x = 0\) (must be an equation) A1 N1
[1 mark]
METHOD 1
attempt to substitute \(3\) into \(h\) (seen anywhere) (M1)
eg \(h(3),{\text{ }}\frac{5}{{3 + 2}}\)
correct equation (A1)
eg \(a = \frac{5}{{3 + 2}},{\text{ }}h(3) = a\)
\(a = 1\) A1 N2
[3 marks]
METHOD 2
attempt to find inverse (may be seen in (d)) (M1)
eg \(x = \frac{5}{{y + 2}},{\text{ }}{h^{ – 1}} = \frac{5}{x} – 2,{\text{ }}\frac{5}{x} + 2\)
correct equation, \(\frac{5}{x} – 2 = 3\) (A1)
\(a = 1\) A1 N2
[3 marks]
Question
The following diagram shows the graph of \(y = f(x)\), for \( – 4 \le x \le 5\).
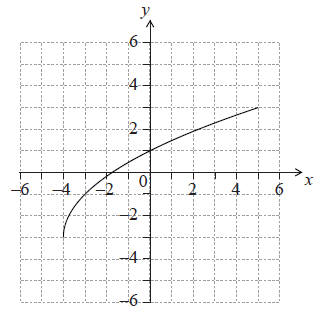
Write down the value of \(f( – 3)\).
Write down the value of \({f^{ – 1}}(1)\).
Find the domain of \({f^{ – 1}}\).
On the grid above, sketch the graph of \({f^{ – 1}}\).
Answer/Explanation
Markscheme
\(f( – 3) = – 1\) A1 N1
[1 mark]
\({f^{ – 1}}(1) = 0\) (accept \(y = 0\)) A1 N1
[1 mark]
domain of \({f^{ – 1}}\) is range of \(f\) (R1)
eg \({\text{R}}f = {\text{D}}{f^{ – 1}}\)
correct answer A1 N2
eg \( – 3 \leqslant x \leqslant 3,{\text{ }}x \in [ – 3,{\text{ }}3]{\text{ (accept }} – 3 < x < 3,{\text{ }} – 3 \leqslant y \leqslant 3)\)
[2 marks]
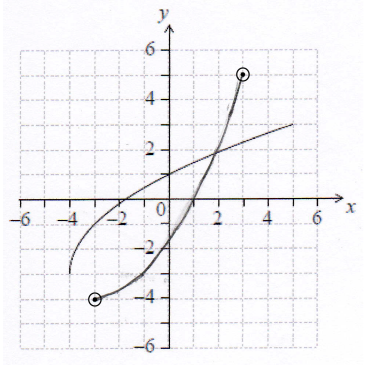A1A1 N2
Note: Graph must be approximately correct reflection in \(y = x\).
Only if the shape is approximately correct, award the following:
A1 for x-intercept at \(1\), and A1 for endpoints within circles.
[2 marks]
Question
Let \(f(x) = 8x + 3\) and \(g(x) = 4x\), for \(x \in \mathbb{R}\).
Write down \(g(2)\).
Find \((f \circ g)(x)\).
Find \({f^{ – 1}}(x)\).
Answer/Explanation
Markscheme
\(g(2) = 8\) A1 N1
[1 mark]
attempt to form composite (in any order) (M1)
eg\(\,\,\,\,\,\)\(f(4x),{\text{ }}4 \times (8x + 3)\)
\((f \circ g)(x) = 32x + 3\) A1 N2
[2 marks]
interchanging \(x\) and \(y\) (may be seen at any time) (M1)
eg\(\,\,\,\,\,\)\(x = 8y + 3\)
\({f^{ – 1}}(x) = \frac{{x – 3}}{8}\,\,\,\,\,\left( {{\text{accept }}\frac{{x – 3}}{8},{\text{ }}y = \frac{{x – 3}}{8}} \right)\) A1 N2
[2 marks]
Question
The following diagram shows the graph of a function \(f\), with domain \( – 2 \leqslant x \leqslant 4\).
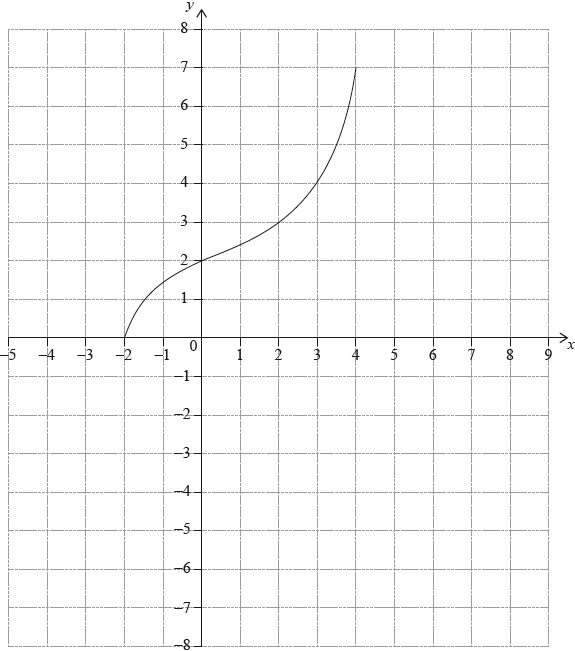
The points \(( – 2,{\text{ }}0)\) and \((4,{\text{ }}7)\) lie on the graph of \(f\).
Write down the range of \(f\).
Write down \(f(2)\);
Write down \({f^{ – 1}}(2)\).
On the grid, sketch the graph of \({f^{ – 1}}\).
Answer/Explanation
Markscheme
correct range (do not accept \(0 \leqslant x \leqslant 7\)) A1 N1
eg\(\,\,\,\,\,\)\([0,{\text{ }}7],{\text{ }}0 \leqslant y \leqslant 7\)
[1 mark]
\(f(2) = 3\) A1 N1
[1 mark]
\({f^{ – 1}}(2) = 0\) A1 N1
[1 mark]
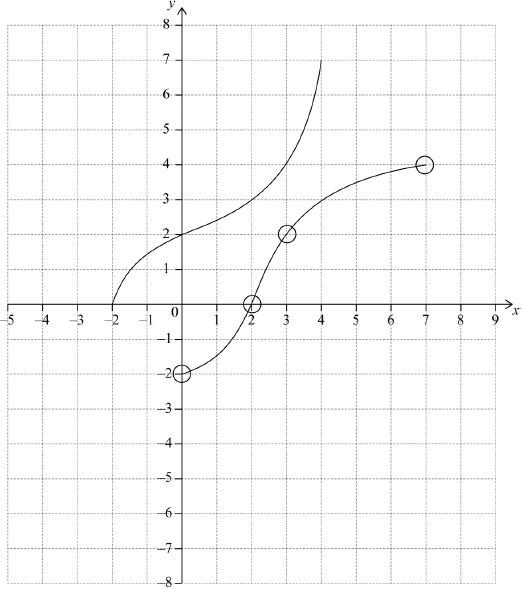A1A1A1 N3
Notes: Award A1 for both end points within circles,
A1 for images of \((2,{\text{ }}3)\) and \((0,{\text{ }}2)\) within circles,
A1 for approximately correct reflection in \(y = x\), concave up then concave down shape (do not accept line segments).
[3 marks]
Question
Let \(f\left( x \right) = \sqrt {x + 2} \) for x ≥ 2 and g(x) = 3x − 7 for \(x \in \mathbb{R}\).
Write down f (14).
Find \(\left( {g \circ f} \right)\) (14).
Find g−1(x).
Answer/Explanation
Markscheme
f (14) = 4 A1 N1
[1 mark]
attempt to substitute (M1)
eg g (4), 3 × 4 − 7
5 A1 N2
[2 marks]
interchanging x and y (seen anywhere) (M1)
eg x = 3y − 7
evidence of correct manipulation (A1)
eg x + 7 = 3y
\({g^{ – 1}}\left( x \right) = \frac{{x + 7}}{3}\) A1 N3
[3 marks]
Question
Consider a function f (x) , for −2 ≤ x ≤ 2 . The following diagram shows the graph of f.
Write down the value of f (0).
Write down the value of f −1 (1).
Write down the range of f −1.
On the grid above, sketch the graph of f −1.
Answer/Explanation
Markscheme
\(f\left( 0 \right) = – \frac{1}{2}\) A1 N1
[1 mark]
f −1 (1) = 2 A1 N1
[1 mark]
−2 ≤ y ≤ 2, y∈ [−2, 2] (accept −2 ≤ x ≤ 2) A1 N1
[1 mark]
A1A1A1A1 N4
Note: Award A1 for evidence of approximately correct reflection in y = x with correct curvature.
(y = x does not need to be explicitly seen)
Only if this mark is awarded, award marks as follows:
A1 for both correct invariant points in circles,
A1 for the three other points in circles,
A1 for correct domain.
[4 marks]