Download IITian Academy App for accessing Online Mock Tests and More..
Question
Let \(f(x) = 3x\) , \(g(x) = 2x – 5\) and \(h(x) = (f \circ g)(x)\) .
Find \(h(x)\) .
Find \({h^{ – 1}}(x)\) .
Answer/Explanation
Markscheme
attempt to form composite (M1)
e.g. \(f(2x – 5)\)
\(h(x) = 6x – 15\) A1 N2
[2 marks]
interchanging x and y (M1)
evidence of correct manipulation (A1)
e.g. \(y + 15 = 6x\) , \(\frac{x}{6} = y – \frac{5}{2}\)
\({h^{ – 1}}(x) = \frac{{x + 15}}{6}\) A1 N3
[3 marks]
Question
Let \(f(x) = 2x + 4\) and \(g(x) = 7{x^2}\) .
Find \({f^{ – 1}}(x)\) .
Find \((f \circ g)(x)\) .
Find \((f \circ g)(3.5)\) .
Answer/Explanation
Markscheme
interchanging x and y (may be seen at any time) (M1)
evidence of correct manipulation (A1)
e.g. \(x = 2y + 4\)
\({f^{ – 1}}(x) = \frac{{x – 4}}{2}\) (accept \(y = \frac{{x – 4}}{2},\frac{{x – 4}}{2}\) ) A1 N2
[3 marks]
attempt to form composite (in any order) (M1)
e.g. \(f(7{x^2}){\text{, }}2(7{x^2}) + 4{\text{, }}7{(2x + 4)^2}\)
\((f \circ g)(x) = 14{x^2} + 4\) A1 N2
correct substitution (A1)
e.g. \(7 \times {3.5^2}\) , \(14{(3.5)^2} + 4\)
\((f \circ g)(3.5) = 175.5\) (accept 176) A1 N2
[2 marks]
Question
Let \(f(x) = \ln x\) and \(g(x) = 3 + \ln \left( {\frac{x}{2}} \right)\), for \(x > 0\).
The graph of \(g\) can be obtained from the graph of \(f\) by two transformations:
\[\begin{array}{*{20}{l}} {{\text{a horizontal stretch of scale factor }}q{\text{ followed by}}} \\ {{\text{a translation of }}\left( {\begin{array}{*{20}{c}} h \\ k \end{array}} \right).} \end{array}\]
Let \(h(x) = g(x) \times \cos (0.1x)\), for \(0 < x < 4\). The following diagram shows the graph of \(h\) and the line \(y = x\).
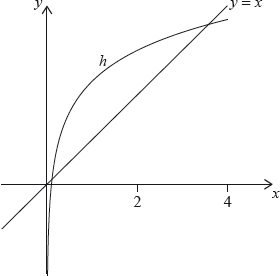
The graph of \(h\) intersects the graph of \({h^{ – 1}}\) at two points. These points have \(x\) coordinates 0.111 and 3.31 correct to three significant figures.
Write down the value of \(q\);
Write down the value of \(h\);
Write down the value of \(k\).
Find \(\int_{0.111}^{3.31} {\left( {h(x) – x} \right){\text{d}}x} \).
Hence, find the area of the region enclosed by the graphs of \(h\) and \({h^{ – 1}}\).
Let \(d\) be the vertical distance from a point on the graph of \(h\) to the line \(y = x\). There is a point \({\text{P}}(a,{\text{ }}b)\) on the graph of \(h\) where \(d\) is a maximum.
Find the coordinates of P, where \(0.111 < a < 3.31\).
Answer/Explanation
Markscheme
\(q = 2\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
\(h = 0\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
\(k = 3\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
2.72409
2.72 A2 N2
[2 marks]
recognizing area between \(y = x\) and \(h\) equals 2.72 (M1)
eg\(\,\,\,\,\,\)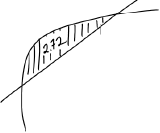
recognizing graphs of \(h\) and \({h^{ – 1}}\) are reflections of each other in \(y = x\) (M1)
eg\(\,\,\,\,\,\)area between \(y = x\) and \(h\) equals between \(y = x\) and \({h^{ – 1}}\)
\(2 \times 2.72\int_{0.111}^{3.31} {\left( {x – {h^{ – 1}}(x)} \right){\text{d}}x = 2.72} \)
5.44819
5.45 A1 N3
[??? marks]
valid attempt to find \(d\) (M1)
eg\(\,\,\,\,\,\)difference in \(y\)-coordinates, \(d = h(x) – x\)
correct expression for \(d\) (A1)
eg\(\,\,\,\,\,\)\(\left( {\ln \frac{1}{2}x + 3} \right)(\cos 0.1x) – x\)
valid approach to find when \(d\) is a maximum (M1)
eg\(\,\,\,\,\,\)max on sketch of \(d\), attempt to solve \(d’ = 0\)
0.973679
\(x = 0.974\) A2 N4
substituting their \(x\) value into \(h(x)\) (M1)
2.26938
\(y = 2.27\) A1 N2
[7 marks]
Question
Let \(h(x) = \frac{{2x – 1}}{{x + 1}}\) , \(x \ne – 1\) .
Find \({h^{ – 1}}(x)\) .
(i) Sketch the graph of h for \( – 4 \le x \le 4\) and \( – 5 \le y \le 8\) , including any asymptotes.
(ii) Write down the equations of the asymptotes.
(iii) Write down the x-intercept of the graph of h .
Let R be the region in the first quadrant enclosed by the graph of h , the x-axis and the line \(x = 3\).
(i) Find the area of R.
(ii) Write down an expression for the volume obtained when R is revolved through \({360^ \circ }\) about the x-axis.
Answer/Explanation
Markscheme
\(y = \frac{{2x – 1}}{{x + 1}}\)
interchanging x and y (seen anywhere) M1
e.g. \(x = \frac{{2y – 1}}{{y + 1}}\)
correct working A1
e.g. \(xy + x = 2y – 1\)
collecting terms A1
e.g. \(x + 1 = 2y – xy\) , \(x + 1 = y(2 – x)\)
\({h^{ – 1}}(x) = \frac{{x + 1}}{{2 – x}}\) A1 N2
[4 marks]
A1A1A1A1 N4
Note: Award A1 for approximately correct intercepts, A1 for correct shape, A1 for asymptotes, A1 for approximately correct domain and range.
(ii) \(x = – 1\) , \(y = 2\) A1A1 N2
(iii) \(\frac{1}{2}\) A1 N1
[7 marks]
(i) \({\text{area}} = 2.06\) A2 N2
(ii) attempt to substitute into volume formula (do not accept \(\pi \int_a^b {{y^2}{\rm{d}}x} \) ) M1
volume \( = \pi {\int_{\frac{1}{2}}^3 {\left( {\frac{{2x – 1}}{{x + 1}}} \right)} ^2}{\rm{d}}x\) A2 N3
[5 marks]