Download IITian Academy App for accessing Online Mock Tests and More..
Question
Let \(f(x) = 4{\tan ^2}x – 4\sin x\) , \( – \frac{\pi }{3} \le x \le \frac{\pi }{3}\) .
On the grid below, sketch the graph of \(y = f(x)\) .
Solve the equation \(f(x) = 1\) .
Answer/Explanation
Markscheme
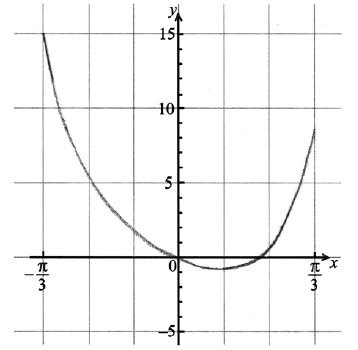A1A1A1 N3
Note: Award A1 for passing through \((0{\text{, }}0)\), A1 for correct shape, A1 for a range of approximately \( – 1\) to 15.
[3 marks]
evidence of attempt to solve \(f(x) = 1\) (M1)
e.g. line on sketch, using \(\tan x = \frac{{\sin x}}{{\cos x}}\)
\(x = – 0.207\) , \(x = 0.772\) A1A1 N3
[3 marks]
Question
Let \(f(x) = x\cos (x – \sin x)\) , \(0 \le x \le 3\) .
Sketch the graph of f on the following set of axes.
The graph of f intersects the x-axis when \(x = a\) , \(a \ne 0\) . Write down the value of a.
The graph of f is revolved \(360^\circ \) about the x-axis from \(x = 0\) to \(x = a\) . Find the volume of the solid formed.
Answer/Explanation
Markscheme
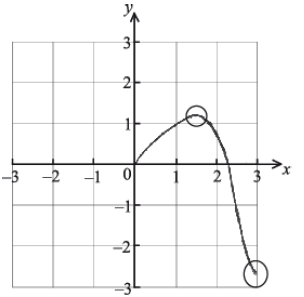A1A2 N3
Notes: Award A1 for correct domain, \(0 \le x \le 3\) . Award A2 for approximately correct shape, with local maximum in circle 1 and right endpoint in circle 2.
[3 marks]
\(a = 2.31\) A1 N1
[1 mark]
evidence of using \(V = \pi {\int {\left[ {f(x)} \right]} ^2}{\rm{d}}x\) (M1)
fully correct integral expression A2
e.g. \(V = \pi {\int_0^{2.31} {\left[ {x\cos (x – \sin x)} \right]} ^2}{\rm{d}}x\) , \(V = \pi {\int_0^{2.31} {\left[ {f(x)} \right]} ^2}{\rm{d}}x\) A1 N2
\(V = 5.90\)
[4 marks]
Question
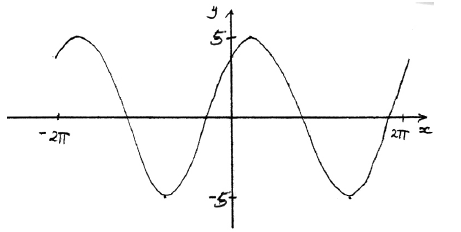
Let \(f(x) = 3\sin x + 4\cos x\) , for \( – 2\pi \le x \le 2\pi \) .
Sketch the graph of f .
Write down
(i) the amplitude;
(ii) the period;
(iii) the x-intercept that lies between \( – \frac{\pi }{2}\) and 0.
Hence write \(f(x)\) in the form \(p\sin (qx + r)\) .
Write down one value of x such that \(f'(x) = 0\) .
Write down the two values of k for which the equation \(f(x) = k\) has exactly two solutions.
Let \(g(x) = \ln (x + 1)\) , for \(0 \le x \le \pi \) . There is a value of x, between \(0\) and \(1\), for which the gradient of f is equal to the gradient of g. Find this value of x.
Answer/Explanation
Markscheme
A1A1A1 N3
Note: Award A1 for approximately sinusoidal shape, A1 for end points approximately correct \(( – 2\pi {\text{, }}4)\) \((2\pi {\text{, }}4)\), A1 for approximately correct position of graph, (y-intercept \((0{\text{, }}4)\), maximum to right of y-axis).
[3 marks]
(i) 5 A1 N1
(ii) \(2\pi \) (6.28) A1 N1
(iii) \( – 0.927\) A1 N1
[3 marks]
\(f(x) = 5\sin (x + 0.927)\) (accept \(p = 5\) , \(q = 1\) , \(r = 0.927\) ) A1A1A1 N3
[3 marks]
evidence of correct approach (M1)
e.g. max/min, sketch of \(f'(x)\) indicating roots
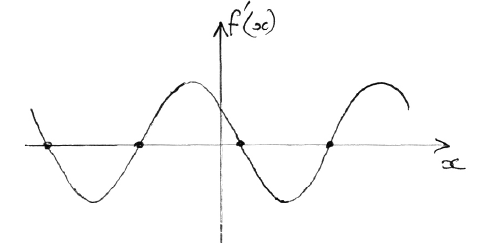
one 3 s.f. value which rounds to one of \( – 5.6\), \( – 2.5\), \(0.64\), \(3.8\) A1 N2
[2 marks]
\(k = – 5\) , \(k = 5\) A1A1 N2
[2 marks]
METHOD 1
graphical approach (but must involve derivative functions) M1
e.g.
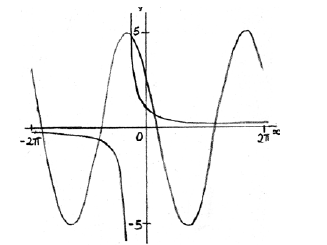
each curve A1A1
\(x = 0.511\) A2 N2
METHOD 2
\(g'(x) = \frac{1}{{x + 1}}\) A1
\(f'(x) = 3\cos x – 4\sin x\) \((5\cos (x + 0.927))\) A1
evidence of attempt to solve \(g'(x) = f'(x)\) M1
\(x = 0.511\) A2 N2
[5 marks]
Question
A farmer wishes to create a rectangular enclosure, ABCD, of area 525 m2, as shown below.
The fencing used for side AB costs \(\$ 11\) per metre. The fencing for the other three sides costs \(\$ 3\) per metre. The farmer creates an enclosure so that the cost is a minimum. Find this minimum cost.
Answer/Explanation
Markscheme
METHOD 1
correct expression for second side, using area = 525 (A1)
e.g. let \({\rm{AB}} = x\) , \({\rm{AD}} = \frac{{525}}{x}\)
attempt to set up cost function using $3 for three sides and $11 for one side (M1)
e.g. \(3({\rm{AD}} + {\rm{BC}} + {\rm{CD}}) + 11{\rm{AB}}\)
correct expression for cost A2
e.g. \(\frac{{525}}{x} \times 3 + \frac{{525}}{x} \times 3 + 11x + 3x\) , \(\frac{{525}}{{{\rm{AB}}}} \times 3 + \frac{{525}}{{{\rm{AB}}}} \times 3 + 11{\rm{AB}} + 3{\rm{AB}}\) , \(\frac{{3150}}{x} + 14x\)
EITHER
sketch of cost function (M1)
identifying minimum point (A1)
e.g. marking point on graph, \(x = 15\)
minimum cost is 420 (dollars) A1 N4
OR
correct derivative (may be seen in equation below) (A1)
e.g. \(C'(x) = \frac{{ – 1575}}{{{x^2}}} + \frac{{ – 1575}}{{{x^2}}} + 14\)
setting their derivative equal to 0 (seen anywhere) (M1)
e.g. \(\frac{{ – 3150}}{{{x^2}}} + 14 = 0\)
minimum cost is 420 (dollars) A1 N4
METHOD 2
correct expression for second side, using area = 525 (A1)
e.g. let \({\rm{AD}} = x\) , \({\rm{AB}} = \frac{{525}}{x}\)
attempt to set up cost function using \(\$ 3\) for three sides and \(\$ 11\) for one side (M1)
e.g. \(3({\rm{AD}} + {\rm{BC}} + {\rm{CD}}) + 11{\rm{AB}}\)
correct expression for cost A2
e.g. \(3\left( {x + x + \frac{{525}}{x}} \right) + \frac{{525}}{x} \times 11\) , \(3\left( {{\rm{AD}} + {\rm{AD}} + \frac{{525}}{{{\rm{AD}}}}} \right) + \frac{{525}}{{{\rm{AD}}}} \times 11\) , \(6x + \frac{{7350}}{x}\)
EITHER
sketch of cost function (M1)
identifying minimum point (A1)
e.g. marking point on graph, \(x = 35\)
minimum cost is 420 (dollars) A1 N4
OR
correct derivative (may be seen in equation below) (A1)
e.g. \(C'(x) = 6 – \frac{{7350}}{{{x^2}}}\)
setting their derivative equal to 0 (seen anywhere) (M1)
e.g. \(6 – \frac{{7350}}{{{x^2}}} = 0\)
minimum cost is 420 (dollars) A1 N4
[7 marks]
Question
Let \(f(x) = 5\cos \frac{\pi }{4}x\) and \(g(x) = – 0.5{x^2} + 5x – 8\) for \(0 \le x \le 9\) .
On the same diagram, sketch the graphs of f and g .
Consider the graph of \(f\) . Write down
(i) the x-intercept that lies between \(x = 0\) and \(x = 3\) ;
(ii) the period;
(iii) the amplitude.
Consider the graph of g . Write down
(i) the two x-intercepts;
(ii) the equation of the axis of symmetry.
Let R be the region enclosed by the graphs of f and g . Find the area of R.
Answer/Explanation
Markscheme
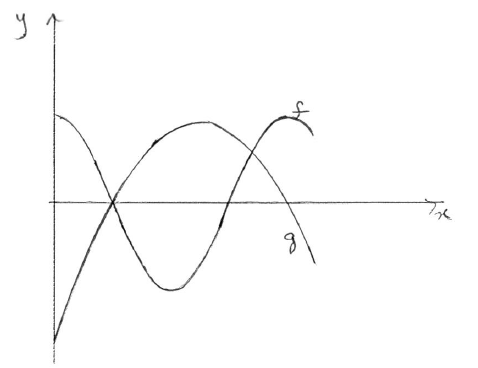A1A1A1 N3
Note: Award A1 for f being of sinusoidal shape, with 2 maxima and one minimum, A1 for g being a parabola opening down, A1 for two intersection points in approximately correct position.
[3 marks]
(i) \((2{\text{, }}0)\) (accept \(x = 2\) ) A1 N1
(ii) \({\text{period}} = 8\) A2 N2
(iii) \({\text{amplitude}} = 5\) A1 N1
[4 marks]
(i) \((2{\text{, }}0)\) , \((8{\text{, }}0)\) (accept \(x = 2\) , \(x = 8\) ) A1A1 N1N1
(ii) \(x = 5\) (must be an equation) A1 N1
[3 marks]
METHOD 1
intersect when \(x = 2\) and \(x = 6.79\) (may be seen as limits of integration) A1A1
evidence of approach (M1)
e.g. \(\int {g – f} \) , \(\int {f(x){\rm{d}}x – \int {g(x){\rm{d}}x}}\) , \(\int_2^{6.79} {\left( {( – 0.5{x^2} + 5x – 8) – \left( {5\cos \frac{\pi }{4}x} \right)} \right)}\)
\({\text{area}} = 27.6\) A2 N3
METHOD 2
intersect when \(x = 2\) and \(x = 6.79\) (seen anywhere) A1A1
evidence of approach using a sketch of g and f , or \(g – f\) . (M1)
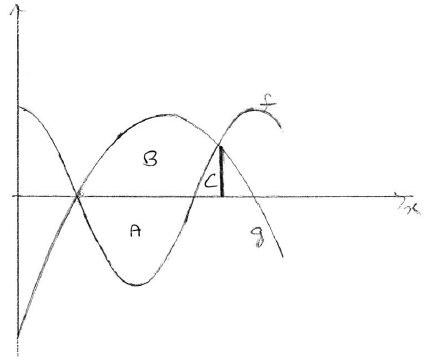
e.g. area = \(A + B – C\) , \(12.7324 + 16.0938 – 1.18129 \ldots \)
\({\text{area}} = 27.6\) A2 N3
[5 marks]
Question
Let \(f(x) = \frac{{20x}}{{{{\rm{e}}^{0.3x}}}}\) , for \(0 \le x \le 20\) .
Sketch the graph of f .
(i) Write down the x-coordinate of the maximum point on the graph of f .
(ii) Write down the interval where f is increasing.
Show that \(f'(x) = \frac{{20 – 6x}}{{{{\rm{e}}^{0.3x}}}}\) .
Find the interval where the rate of change of f is increasing.
Answer/Explanation
Markscheme
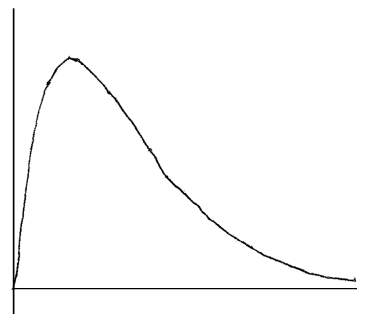A1A1A1 N3
Note: Award A1 for approximately correct shape with inflexion/change of curvature, A1 for maximum skewed to the left, A1 for asymptotic behaviour to the right.
[3 marks]
(i) \(x = 3.33\) A1 N1
(ii) correct interval, with right end point \(3\frac{1}{3}\) A1A1 N2
e.g. \(0 < x \le 3.33\) , \(0 \le x < 3\frac{1}{3}\)
Note: Accept any inequalities in the right direction.
[3 marks]
valid approach (M1)
e.g. quotient rule, product rule
2 correct derivatives (must be seen in product or quotient rule) (A1)(A1)
e.g. \(20\) , \(0.3{{\rm{e}}^{0.3x}}\) or \( – 0.3{{\rm{e}}^{ – 0.3x}}\)
correct substitution into product or quotient rule A1
e.g. \(\frac{{20{{\rm{e}}^{0.3x}} – 20x(0.3){{\rm{e}}^{0.3x}}}}{{{{({{\rm{e}}^{0.3x}})}^2}}}\) , \(20{{\rm{e}}^{ – 0.3x}} + 20x( – 0.3){{\rm{e}}^{ – 0.3x}}\)
correct working A1
e.g. \(\frac{{20{{\rm{e}}^{0.3x}} – 6x{{\rm{e}}^{0.3x}}}}{{{{\rm{e}}^{0.6x}}}}\) , \(\frac{{{{\rm{e}}^{0.3x}}(20 – 20x(0.3))}}{{{{{\rm{(}}{{\rm{e}}^{0.3x}})}^2}}}\) , \({{\rm{e}}^{ – 0.3x}}(20 + 20x( – 0.3))\)
\(f'(x) = \frac{{20 – 6x}}{{{{\rm{e}}^{0.3x}}}}\) AG N0
[5 marks]
consideration of \(f’\) or \(f”\) (M1)
valid reasoning R1
e.g. sketch of \(f’\) , \(f”\) is positive, \(f” = 0\) , reference to minimum of \(f’\)
correct value \(6.6666666 \ldots \) \(\left( {6\frac{2}{3}} \right)\) (A1)
correct interval, with both endpoints A1 N3
e.g. \(6.67 < x \le 20\) , \(6\frac{2}{3} \le x < 20\)
[4 marks]
Question
A particle’s displacement, in metres, is given by \(s(t) = 2t\cos t\) , for \(0 \le t \le 6\) , where t is the time in seconds.
On the grid below, sketch the graph of \(s\) .
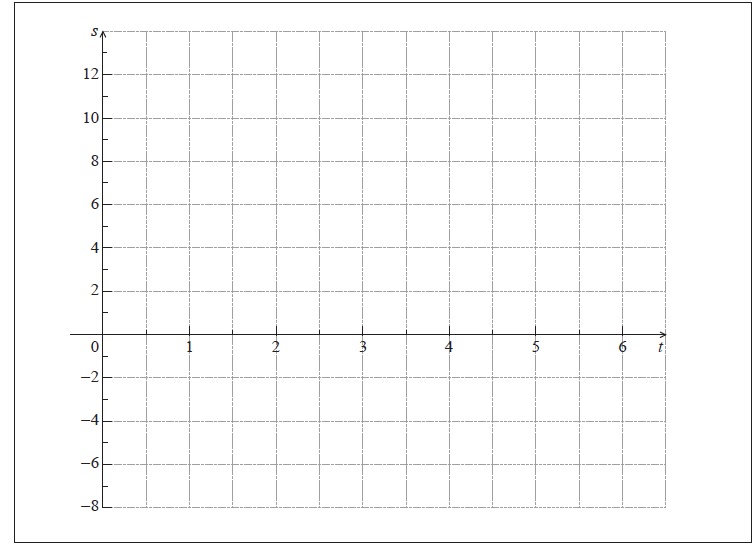
Find the maximum velocity of the particle.
Answer/Explanation
Markscheme
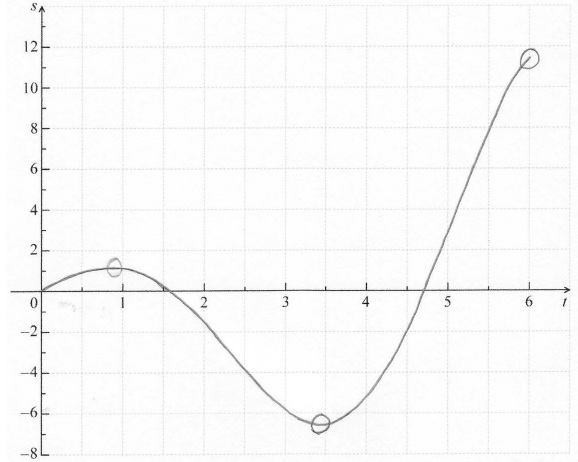A1A1A1A1 N4
Note: Award A1 for approximately correct shape (do not accept line segments).
Only if this A1 is awarded, award the following:
A1 for maximum and minimum within circles,
A1 for x-intercepts between 1 and 2 and between 4 and 5,
A1 for left endpoint at \((0{\text{, }}0)\) and right endpoint within circle.
[4 marks]
appropriate approach (M1)
e.g. recognizing that \(v = s’\) , finding derivative, \(a = s”\)
valid method to find maximum (M1)
e.g. sketch of \(v\) , \(v'(t) = 0\) , \(t = 5.08698 \ldots \)
\(v = 10.20025 \ldots \)
\(v = 10.2\) \([10.2{\text{, }}10.3]\) A1 N2
[3 marks]
Question
The velocity of a particle in ms−1 is given by \(v = {{\rm{e}}^{\sin t}} – 1\) , for \(0 \le t \le 5\) .
On the grid below, sketch the graph of \(v\) .
Find the total distance travelled by the particle in the first five seconds.
Write down the positive \(t\)-intercept.
Answer/Explanation
Markscheme
A1A1A1 N3
Note: Award A1 for approximately correct shape crossing x-axis with \(3 < x < 3.5\) .
Only if this A1 is awarded, award the following:
A1 for maximum in circle, A1 for endpoints in circle.
[3 marks]
\(t = \pi \) (exact), \(3.14\) A1 N1
[1 mark]
recognizing distance is area under velocity curve (M1)
eg \(s = \int v \) , shading on diagram, attempt to integrate
valid approach to find the total area (M1)
eg \({\text{area A}} + {\text{area B}}\) , \(\int {v{\rm{d}}t – \int {v{\rm{d}}t} } \) , \(\int_0^{3.14} {v{\rm{d}}t + } \int_{3.14}^5 {v{\rm{d}}t} \) , \(\int {\left| v \right|} \)
correct working with integration and limits (accept \({\rm{d}}x\) or missing \({\rm{d}}t\) ) (A1)
eg \(\int_0^{3.14} {v{\rm{d}}t + } \int_5^{3.14} {v{\rm{d}}t} \) , \(3.067 \ldots + 0.878 \ldots \) , \(\int_0^5 {\left| {{{\rm{e}}^{\sin t}} – 1} \right|} \)
distance \( = 3.95\) (m) A1 N3
[4 marks]
Question
Let \(f(x) = {{\rm{e}}^{\frac{x}{4}}}\) and \(g(x) = mx\) , where \(m \ge 0\) , and \( – 5 \le x \le 5\) . Let \(R\) be the region enclosed by the \(y\)-axis, the graph of \(f\) , and the graph of \(g\) .
Let \(m = 1\).
(i) Sketch the graphs of \(f\) and \(g\) on the same axes.
(ii) Find the area of \(R\) .
Find the area of \(R\) .
Consider all values of \(m\) such that the graphs of \(f\) and \(g\) intersect. Find the value of \(m\) that gives the greatest value for the area of \(R\) .
Answer/Explanation
Markscheme
(i)
A1A1 N2
Notes: Award A1 for the graph of \(f\) positive, increasing and concave up.
Award A1 for graph of \(g\) increasing and linear with \(y\)-intercept of \(0\).
Penalize one mark if domain is not [\( – 5\), \(5\)] and/or if \(f\) and \(g\) do not intersect in the first quadrant.
[2 marks]
(ii)
attempt to find intersection of the graphs of \(f\) and \(g\) (M1)
eg \({{\rm{e}}^{\frac{x}{4}}} = x\)
\(x = 1.42961 \ldots \) A1
valid attempt to find area of \(R\) (M1)
eg \(\int {(x – {{\rm{e}}^{\frac{x}{4}}}} ){\rm{d}}x\) , \(\int_0^1 {(g – f)} \) , \(\int {(f – g)} \)
area \( = 0.697\) A2 N3
[5 marks]
attempt to find intersection of the graphs of \(f\) and \(g\) (M1)
eg \({{\rm{e}}^{\frac{x}{4}}} = x\)
\(x = 1.42961 \ldots \) A1
valid attempt to find area of \(R\) (M1)
eg \(\int {(x – {{\rm{e}}^{\frac{x}{4}}}} ){\rm{d}}x\) , \(\int_0^1 {(g – f)} \) , \(\int {(f – g)} \)
area \( = 0.697\) A2 N3
[5 marks]
recognize that area of \(R\) is a maximum at point of tangency (R1)
eg \(m = f'(x)\)
equating functions (M1)
eg \(f(x) = g(x)\) , \({{\rm{e}}^{\frac{x}{4}}} = mx\)
\(f'(x) = \frac{1}{4}{{\rm{e}}^{\frac{x}{4}}}\) (A1)
equating gradients (A1)
eg \(f'(x) = g'(x)\) , \(\frac{1}{4}{{\rm{e}}^{\frac{x}{4}}} = m\)
attempt to solve system of two equations for \(x\) (M1)
eg \(\frac{1}{4}{{\rm{e}}^{\frac{x}{4}}} \times x = {{\rm{e}}^{\frac{x}{4}}}\)
\(x = 4\) (A1)
attempt to find \(m\) (M1)
eg \(f'(4)\) , \(\frac{1}{4}{{\rm{e}}^{\frac{4}{4}}}\)
\(m = \frac{1}{4}e\) (exact), \(0.680\) A1 N3
[8 marks]
Question
A particle moves along a straight line such that its velocity, \(v{\text{ m}}{{\text{s}}^{ – 1}}\), is given by \(v(t) = 10t{{\text{e}}^{ – 1.7t}}\), for \(t \geqslant 0\).
On the grid below, sketch the graph of \(v\), for \(0 \leqslant t \leqslant 4\).
Find the distance travelled by the particle in the first three seconds.
Find the velocity of the particle when its acceleration is zero.
Answer/Explanation
Markscheme
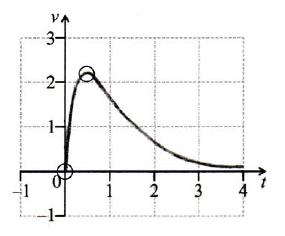A1A2 N3
Notes: Award A1 for approximately correct domain \(0 \leqslant t \leqslant 4\).
The shape must be approximately correct, with maximum skewed left. Only if the shape is approximately correct, award A2 for all the following approximately correct features, in circle of tolerance where drawn (accept seeing correct coordinates for the maximum, even if point outside circle):
Maximum point, passes through origin, asymptotic to \(t\)-axis (but must not touch the axis).
If only two of these features are correct, award A1.
[3 marks]
valid approach (including \(0\) and \(3\)) (M1)
eg \(\int_0^3 {10t{{\text{e}}^{ – 1.7t}}{\text{d}}t,{\text{ }}\int_0^3 {f(x)} } \), area from \(0\) to \(3\) (may be shaded in diagram)
\({\text{distance}} = 3.33{\text{ (m)}}\) A1 N2
[2 marks]
recognizing acceleration is derivative of velocity (R1)
eg \(a = \frac{{{\text{d}}v}}{{{\text{d}}t}}\), attempt to find \(\frac{{{\text{d}}v}}{{{\text{d}}t}}\), reference to maximum on the graph of \(v\)
valid approach to find \(v\) when \(a = 0\) (may be seen on graph) (M1)
eg \(\frac{{{\text{d}}v}}{{{\text{d}}t}} = 0,{\text{ }}10{{\text{e}}^{ – 1.7t}} – 17t{{\text{e}}^{ – 1.7t}} = 0,{\text{ }}t = 0.588\)
\({\text{velocity}} = 2.16{\text{ (m}}{{\text{s}}^{ – 1}})\) A1 N3
Note: Award R1M1A0 for \((0.588, 216)\) if velocity is not identified as final answer
[3 marks]
Question
Let \(f(x) = \cos \left( {\frac{\pi }{4}x} \right) + \sin \left( {\frac{\pi }{4}x} \right),{\text{ for }} – 4 \leqslant x \leqslant 4.\)
Sketch the graph of \(f\).
Find the values of \(x\) where the function is decreasing.
The function \(f\) can also be written in the form \(f(x) = a\sin \left( {\frac{\pi }{4}(x + c)} \right)\), where \(a \in \mathbb{R}\), and \(0 \leqslant c \leqslant 2\). Find the value of \(a\);
The function \(f\) can also be written in the form \(f(x) = a\sin \left( {\frac{\pi }{4}(x + c)} \right)\), where \(a \in \mathbb{R}\), and \(0 \leqslant c \leqslant 2\). Find the value of \(c\).
Answer/Explanation
Markscheme
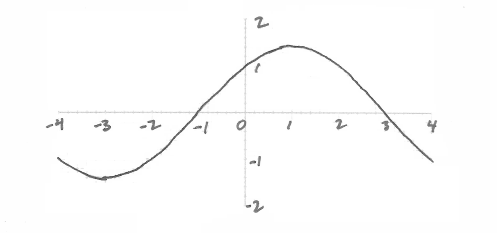A1A1A1 N3
Note: Award A1 for approximately correct sinusoidal shape.
Only if this A1 is awarded, award the following:
A1 for correct domain,
A1 for approximately correct range.
[3 marks]
recognizes decreasing to the left of minimum or right of maximum,
eg \(f'(x) < 0\) (R1)
x-values of minimum and maximum (may be seen on sketch in part (a)) (A1)(A1)
eg \(x = – 3,{\text{ (1, 1.4)}}\)
two correct intervals A1A1 N5
eg \( – 4 < x < – 3,{\text{ }}1 \leqslant x \leqslant 4;{\text{ }}x < – 3,{\text{ }}x \geqslant 1\)
[5 marks]
recognizes that \(a\) is found from amplitude of wave (R1)
y-value of minimum or maximum (A1)
eg (−3, −1.41) , (1, 1.41)
\(a = 1.41421\)
\(a = \sqrt 2 {\text{, (exact), 1.41,}}\) A1 N3
[3 marks]
METHOD 1
recognize that shift for sine is found at x-intercept (R1)
attempt to find x-intercept (M1)
eg \(\cos \left( {\frac{\pi }{4}x} \right) + \sin \left( {\frac{\pi }{4}x} \right) = 0,{\text{ }}x = 3 + 4k,{\text{ }}k \in \mathbb{Z}\)
\(x = – 1\) (A1)
\(c = 1\) A1 N4
METHOD 2
attempt to use a coordinate to make an equation (R1)
eg \(\sqrt 2 \sin \left( {\frac{\pi }{4}c} \right) = 1,{\text{ }}\sqrt 2 \sin \left( {\frac{\pi }{4}(3 – c)} \right) = 0\)
attempt to solve resulting equation (M1)
eg sketch, \(x = 3 + 4k,{\text{ }}k \in \mathbb{Z}\)
\(x = – 1\) (A1)
\(c = 1\) A1 N4
[4 marks]
Question
Let \(G(x) = 95{{\text{e}}^{( – 0.02x)}} + 40\), for \(20 \le x \le 200\).
On the following grid, sketch the graph of \(G\).
Robin and Pat are planning a wedding banquet. The cost per guest, \(G\) dollars, is modelled by the function \(G(n) = 95{{\text{e}}^{( – 0.02n)}} + 40\), for \(20 \le n \le 200\), where \(n\) is the number of guests.
Calculate the total cost for \(45\) guests.
Answer/Explanation
Markscheme
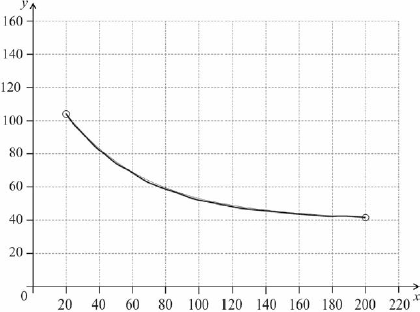A1A1A1 N3
Note: Curve must be approximately correct exponential shape (concave up and decreasing). Only if the shape is approximately correct, award the following:
A1 for left endpoint in circle,
A1 for right endpoint in circle,
A1 for asymptotic to \(y = 40\) (must not go below \(y = 40\)).
[3 marks]
attempt to find \(G(45)\) (M1)
eg\(\;\;\;78.6241\), value read from their graph
multiplying cost times number of people (M1)
eg\(\;\;\;45 \times 78.6241,{\text{ }}G(45) \times 45\)
\(3538.08\)
\(3540\) (dollars) A1 N2
[3 marks]
Total [6 marks]
Question
Let \(f(x) = {{\text{e}}^{x + 1}} + 2\), for \( – 4 \le x \le 1\).
On the following grid, sketch the graph of \(f\).
The graph of \(f\) is translated by the vector \(\left( {\begin{array}{*{20}{c}} 3 \\ { – 1} \end{array}} \right)\) to obtain the graph of a function \(g\).
Find an expression for \(g(x)\).
Answer/Explanation
Markscheme
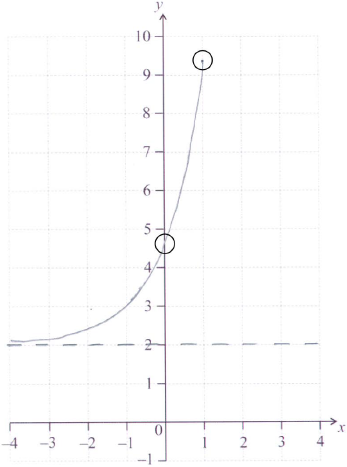1A1A1 N3
Note: Curve must be approximately correct exponential shape (increasing and concave up). Only if the shape is approximately correct, award the following:
A1 for right end point in circle,
A1 for \(y\)-intercept in circle,
A1 for asymptotic to \(y = 2\), (must be above \(y = 2\)).
[3 marks]
valid attempt to find \(g\) (M1)
eg\(\;\;\;f(x – 3) – 1,{\text{ }}g(x) = {{\text{e}}^{x + 1 – 3}} + 2 – 1,{\text{ }}{{\text{e}}^{x + 1 – 3}},{\text{ }}2 – 1\), sketch
\(g(x) = {{\text{e}}^{x – 2}} + 1\) A2 N3
[3 marks]
Total [6 marks]
Question
Let \(f(x) = 0.225{x^3} – 2.7x\), for \( – 3 \leqslant x \leqslant 3\). There is a local minimum point at A.
On the following grid,
Find the coordinates of A.
(i) sketch the graph of \(f\), clearly indicating the point A;
(ii) sketch the tangent to the graph of \(f\) at A.
Answer/Explanation
Markscheme
\({\text{A }}(2,{\text{ }}-3.6)\) A1A1 N2
[2 marks]
(i) (ii)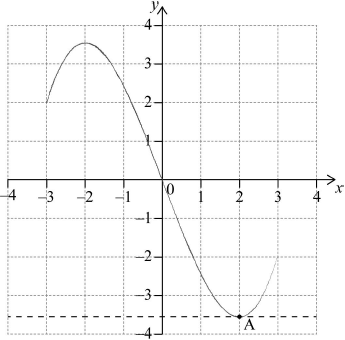 
A1
A1A1A1 N4
A1 N1
Notes: (i) Award A1 for correct cubic shape with correct curvature.
Only if this A1 is awarded, award the following:
A1 for passing through their point A and the origin,
A1 for endpoints,
A1 for maximum.
(ii) Award A1 for horizontal line through their A.
[5 marks]
Question
Let \(f(x) = {x^2} – 1\) and \(g(x) = {x^2} – 2\), for \(x \in \mathbb{R}\).
Show that \((f \circ g)(x) = {x^4} – 4{x^2} + 3\).
On the following grid, sketch the graph of \((f \circ g)(x)\), for \(0 \leqslant x \leqslant 2.25\).
The equation \((f \circ g)(x) = k\) has exactly two solutions, for \(0 \leqslant x \leqslant 2.25\). Find the possible values of \(k\).
Answer/Explanation
Markscheme
attempt to form composite in either order (M1)
eg\(\,\,\,\,\,\)\(f({x^2} – 2),{\text{ }}{({x^2} – 1)^2} – 2\)
\(({x^4} – 4{x^2} + 4) – 1\) A1
\((f \circ g)(x) = {x^4} – 4{x^2} + 3\) AG N0
[2 marks]
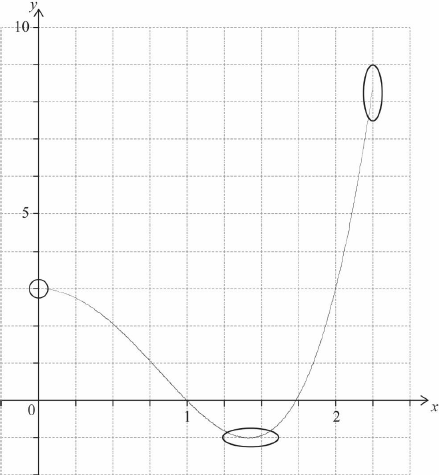A1
A1A1 N3
Note: Award A1 for approximately correct shape which changes from concave down to concave up. Only if this A1 is awarded, award the following:
A1 for left hand endpoint in circle and right hand endpoint in oval,
A1 for minimum in oval.
[3 marks]
evidence of identifying max/min as relevant points (M1)
eg\(\,\,\,\,\,\)\(x = 0,{\text{ }}1.41421,{\text{ }}y = – 1,{\text{ }}3\)
correct interval (inclusion/exclusion of endpoints must be correct) A2 N3
eg\(\,\,\,\,\,\)\( – 1 < k \leqslant 3,{\text{ }}\left] { – 1,{\text{ 3}}} \right],{\text{ }}( – 1,{\text{ }}3]\)
[3 marks]
Question
Let \(f(x) = \frac{{6{x^2} – 4}}{{{{\text{e}}^x}}}\), for \(0 \leqslant x \leqslant 7\).
Find the \(x\)-intercept of the graph of \(f\).
The graph of \(f\) has a maximum at the point A. Write down the coordinates of A.
On the following grid, sketch the graph of \(f\).
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(f(x) = 0,{\text{ }} \pm 0.816\)
0.816496
\(x = \sqrt {\frac{2}{3}} \) (exact), 0.816 A1 N2
[2 marks]
\((2.29099,{\text{ }}2.78124)\)
\({\text{A}}(2.29,{\text{ }}2.78)\) A1A1 N2
[2 marks]
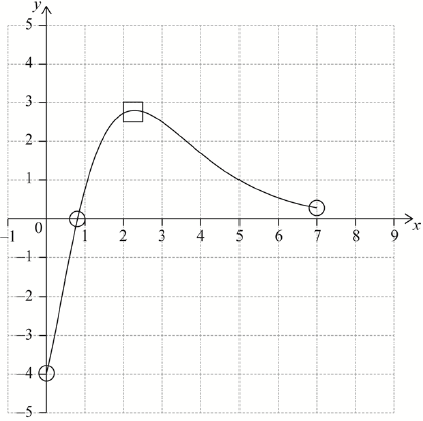A1A1A1 N3
Notes: Award A1 for correct domain and endpoints at \(x = 0\) and \(x = 7\) in circles,
A1 for maximum in square,
A1 for approximately correct shape that passes through their \(x\)-intercept in circle and has changed from concave down to concave up between 2.29 and 7.
[3 marks]
Question
Let g(x) = −(x − 1)2 + 5.
Let f(x) = x2. The following diagram shows part of the graph of f.
The graph of g intersects the graph of f at x = −1 and x = 2.
Write down the coordinates of the vertex of the graph of g.
On the grid above, sketch the graph of g for −2 ≤ x ≤ 4.
Find the area of the region enclosed by the graphs of f and g.
Answer/Explanation
Markscheme
(1,5) (exact) A1 N1
[1 mark]
A1A1A1 N3
Note: The shape must be a concave-down parabola.
Only if the shape is correct, award the following for points in circles:
A1 for vertex,
A1 for correct intersection points,
A1 for correct endpoints.
[3 marks]
integrating and subtracting functions (in any order) (M1)
eg \(\int {f – g} \)
correct substitution of limits or functions (accept missing dx, but do not accept any errors, including extra bits) (A1)
eg \(\int_{ – 1}^2 {g – f,\,\,\int { – {{\left( {x – 1} \right)}^2}} } + 5 – {x^2}\)
area = 9 (exact) A1 N2
[3 marks]
Question
Let \(f(x) = 4x – {{\rm{e}}^{x – 2}} – 3\) , for \(0 \le x \le 5\) .
Find the x-intercepts of the graph of f .
On the grid below, sketch the graph of f .
Write down the gradient of the graph of f at \(x = 3\) .
Answer/Explanation
Markscheme
intercepts when \(f(x) = 0\) M1
(0.827, 0) (4.78, 0) (accept \(x = 0.827\), \(x = 4.78\) ) A1A1 N3
[3 marks]
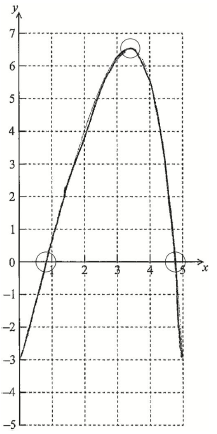A1A1A1 N3
Note: Award A1 for maximum point in circle, A1 for x-intercepts in circles, A1 for correct shape (y approximately greater than \( – 3.14\)).
[3 marks]
gradient is 1.28 A1 N1
[1 mark]
Question
Let \(h(x) = \frac{{2x – 1}}{{x + 1}}\) , \(x \ne – 1\) .
Find \({h^{ – 1}}(x)\) .
(i) Sketch the graph of h for \( – 4 \le x \le 4\) and \( – 5 \le y \le 8\) , including any asymptotes.
(ii) Write down the equations of the asymptotes.
(iii) Write down the x-intercept of the graph of h .
Let R be the region in the first quadrant enclosed by the graph of h , the x-axis and the line \(x = 3\).
(i) Find the area of R.
(ii) Write down an expression for the volume obtained when R is revolved through \({360^ \circ }\) about the x-axis.
Answer/Explanation
Markscheme
\(y = \frac{{2x – 1}}{{x + 1}}\)
interchanging x and y (seen anywhere) M1
e.g. \(x = \frac{{2y – 1}}{{y + 1}}\)
correct working A1
e.g. \(xy + x = 2y – 1\)
collecting terms A1
e.g. \(x + 1 = 2y – xy\) , \(x + 1 = y(2 – x)\)
\({h^{ – 1}}(x) = \frac{{x + 1}}{{2 – x}}\) A1 N2
[4 marks]
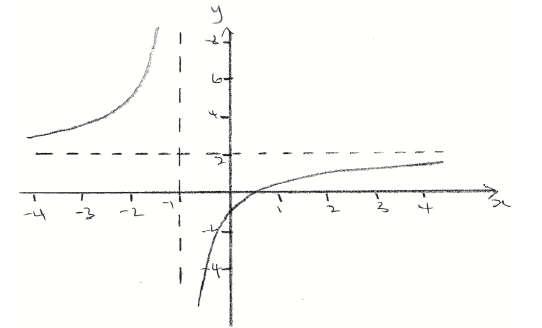A1A1A1A1 N4
Note: Award A1 for approximately correct intercepts, A1 for correct shape, A1 for asymptotes, A1 for approximately correct domain and range.
(ii) \(x = – 1\) , \(y = 2\) A1A1 N2
(iii) \(\frac{1}{2}\) A1 N1
[7 marks]
(i) \({\text{area}} = 2.06\) A2 N2
(ii) attempt to substitute into volume formula (do not accept \(\pi \int_a^b {{y^2}{\rm{d}}x} \) ) M1
volume \( = \pi {\int_{\frac{1}{2}}^3 {\left( {\frac{{2x – 1}}{{x + 1}}} \right)} ^2}{\rm{d}}x\) A2 N3
[5 marks]
Question
A rock falls off the top of a cliff. Let \(h\) be its height above ground in metres, after \(t\) seconds.
The table below gives values of \(h\) and \(t\) .
Jane thinks that the function \(f(t) = – 0.25{t^3} – 2.32{t^2} + 1.93t + 106\) is a suitable model for the data. Use Jane’s model to
(i) write down the height of the cliff;
(ii) find the height of the rock after 4.5 seconds;
(iii) find after how many seconds the height of the rock is \(30{\text{ m}}\).
Kevin thinks that the function \(g(t) = – 5.2{t^2} + 9.5t + 100\) is a better model for the data. Use Kevin’s model to find when the rock hits the ground.
(i) On graph paper, using a scale of 1 cm to 1 second, and 1 cm to 10 m, plot the data given in the table.
(ii) By comparing the graphs of f and g with the plotted data, explain which function is a better model for the height of the falling rock.
Answer/Explanation
Markscheme
(i) \(106{\text{ m}}\) A1 N1
(ii) substitute \(t = 4.5\) M1
\(h = 44.9{\text{ m}}\) A1 N2
(iii) set up suitable equation M1
e.g. \(f(t) = 30\)
\(t = 4.91\) A1 N1
[5 marks]
recognizing that height is 0 A1
set up suitable equation M1
e.g. \(g(t) = 0\)
\(t = 5.39{\text{ secs}}\) A1 N2
[3 marks]
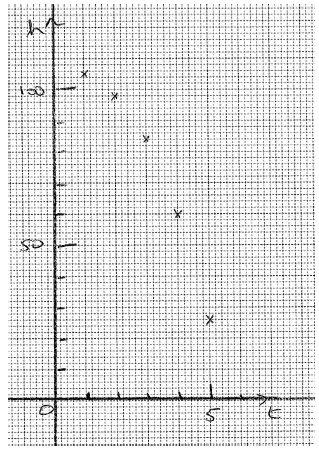A1A2 N3
Note: Award A1 for correct scales on axes, A2 for 5 correct points, A1 for 3 or 4 correct points.
(ii) Jane’s function, with 2 valid reasons A1R1R1 N3
e.g. Jane’s passes very close to all the points, Kevin’s has the rock clearly going up initially – not possible if rock falls
Note: Although Jane’s also goes up initially, it only goes up very slightly, and so is the better model.
[6 marks]