Download IITian Academy App for accessing Online Mock Tests and More..
Question
Let \(f(x) = {{\rm{e}}^x}(1 – {x^2})\) .
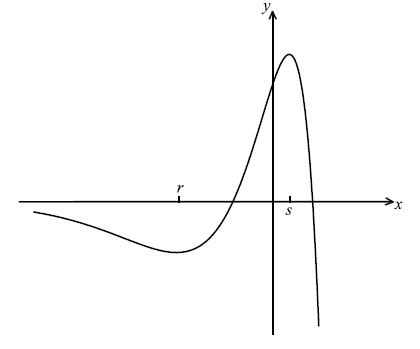
Part of the graph of \(y = f(x)\), for \( – 6 \le x \le 2\) , is shown below. The x-coordinates of the local minimum and maximum points are r and s respectively.
Show that \(f'(x) = {{\rm{e}}^x}(1 – 2x – {x^2})\) .
Write down the equation of the horizontal asymptote.
Write down the value of r and of s.
Let L be the normal to the curve of f at \({\text{P}}(0{\text{, }}1)\) . Show that L has equation \(x + y = 1\) .
Let R be the region enclosed by the curve \(y = f(x)\) and the line L.
(i) Find an expression for the area of R.
(ii) Calculate the area of R.
Answer/Explanation
Markscheme
evidence of using the product rule M1
\(f'(x) = {{\rm{e}}^x}(1 – {x^2}) + {{\rm{e}}^x}( – 2x)\) A1A1
Note: Award A1 for \({{\rm{e}}^x}(1 – {x^2})\) , A1 for \({{\rm{e}}^x}( – 2x)\) .
\(f'(x) = {{\rm{e}}^x}(1 – 2x – {x^2})\) AG N0
[3 marks]
\(y = 0\) A1 N1
[1 mark]
at the local maximum or minimum point
\(f'(x) = 0\) \(({{\rm{e}}^x}(1 – 2x – {x^2}) = 0)\) (M1)
\( \Rightarrow 1 – 2x – {x^2} = 0\) (M1)
\(r = – 2.41\) \(s = 0.414\) A1A1 N2N2
[4 marks]
\(f'(0) = 1\) A1
gradient of the normal \(= – 1\) A1
evidence of substituting into an equation for a straight line (M1)
correct substitution A1
e.g. \(y – 1 = – 1(x – 0)\) , \(y – 1 = – x\) , \(y = – x + 1\)
\(x + y = 1\) AG N0
[4 marks]
(i) intersection points at \(x = 0\) and \(x = 1\) (may be seen as the limits) (A1)
approach involving subtraction and integrals (M1)
fully correct expression A2 N4
e.g. \(\int_0^1 {\left( {{{\rm{e}}^x}(1 – {x^2}) – (1 – x)} \right)} {\rm{d}}x\) , \(\int_0^1 {f(x){\rm{d}}x – \int_0^1 {(1 – x){\rm{d}}x} } \)
(ii) area \(R = 0.5\) A1 N1
[5 marks]
Question
Let \(f(x) = x\cos (x – \sin x)\) , \(0 \le x \le 3\) .
Sketch the graph of f on the following set of axes.
The graph of f intersects the x-axis when \(x = a\) , \(a \ne 0\) . Write down the value of a.
The graph of f is revolved \(360^\circ \) about the x-axis from \(x = 0\) to \(x = a\) . Find the volume of the solid formed.
Answer/Explanation
Markscheme
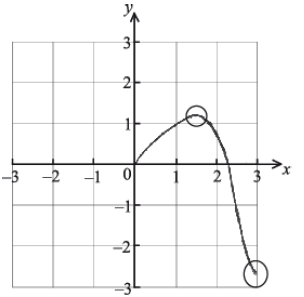A1A2 N3
Notes: Award A1 for correct domain, \(0 \le x \le 3\) . Award A2 for approximately correct shape, with local maximum in circle 1 and right endpoint in circle 2.
[3 marks]
\(a = 2.31\) A1 N1
[1 mark]
evidence of using \(V = \pi {\int {\left[ {f(x)} \right]} ^2}{\rm{d}}x\) (M1)
fully correct integral expression A2
e.g. \(V = \pi {\int_0^{2.31} {\left[ {x\cos (x – \sin x)} \right]} ^2}{\rm{d}}x\) , \(V = \pi {\int_0^{2.31} {\left[ {f(x)} \right]} ^2}{\rm{d}}x\) A1 N2
\(V = 5.90\)
[4 marks]
Question
Let \(f(x) = 3\sin x + 4\cos x\) , for \( – 2\pi \le x \le 2\pi \) .
Sketch the graph of f .
Write down
(i) the amplitude;
(ii) the period;
(iii) the x-intercept that lies between \( – \frac{\pi }{2}\) and 0.
Hence write \(f(x)\) in the form \(p\sin (qx + r)\) .
Write down one value of x such that \(f'(x) = 0\) .
Write down the two values of k for which the equation \(f(x) = k\) has exactly two solutions.
Let \(g(x) = \ln (x + 1)\) , for \(0 \le x \le \pi \) . There is a value of x, between \(0\) and \(1\), for which the gradient of f is equal to the gradient of g. Find this value of x.
Answer/Explanation
Markscheme
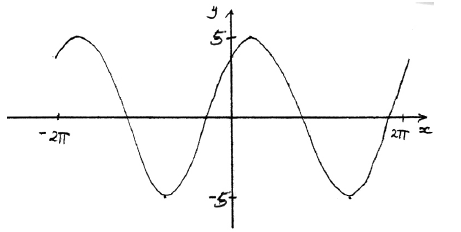A1A1A1 N3
Note: Award A1 for approximately sinusoidal shape, A1 for end points approximately correct \(( – 2\pi {\text{, }}4)\) \((2\pi {\text{, }}4)\), A1 for approximately correct position of graph, (y-intercept \((0{\text{, }}4)\), maximum to right of y-axis).
[3 marks]
(i) 5 A1 N1
(ii) \(2\pi \) (6.28) A1 N1
(iii) \( – 0.927\) A1 N1
[3 marks]
\(f(x) = 5\sin (x + 0.927)\) (accept \(p = 5\) , \(q = 1\) , \(r = 0.927\) ) A1A1A1 N3
[3 marks]
evidence of correct approach (M1)
e.g. max/min, sketch of \(f'(x)\) indicating roots
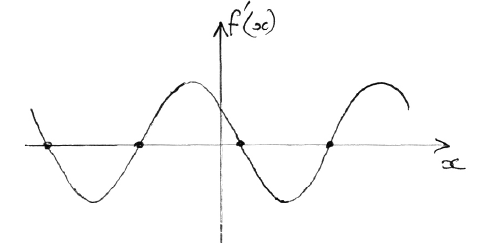
one 3 s.f. value which rounds to one of \( – 5.6\), \( – 2.5\), \(0.64\), \(3.8\) A1 N2
[2 marks]
\(k = – 5\) , \(k = 5\) A1A1 N2
[2 marks]
METHOD 1
graphical approach (but must involve derivative functions) M1
e.g.
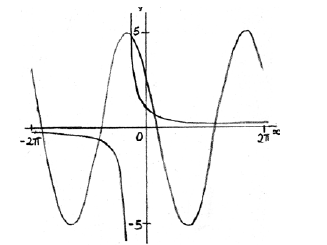
each curve A1A1
\(x = 0.511\) A2 N2
METHOD 2
\(g'(x) = \frac{1}{{x + 1}}\) A1
\(f'(x) = 3\cos x – 4\sin x\) \((5\cos (x + 0.927))\) A1
evidence of attempt to solve \(g'(x) = f'(x)\) M1
\(x = 0.511\) A2 N2
[5 marks]
Question
Let \(f(x) = {{\rm{e}}^x}\sin 2x + 10\) , for \(0 \le x \le 4\) . Part of the graph of f is given below.
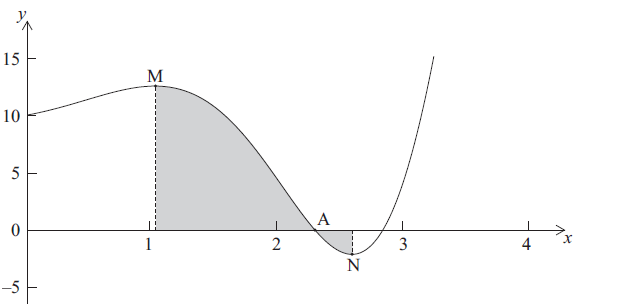
There is an x-intercept at the point A, a local maximum point at M, where \(x = p\) and a local minimum point at N, where \(x = q\) .
Write down the x-coordinate of A.
Find the value of
(i) p ;
(ii) q .
Find \(\int_p^q {f(x){\rm{d}}x} \) . Explain why this is not the area of the shaded region.
Answer/Explanation
Markscheme
\(2.31\) A1 N1
[1 mark]
(i) 1.02 A1 N1
(ii) 2.59 A1 N1
[2 marks]
\(\int_p^q {f(x){\rm{d}}x} = 9.96\) A1 N1
split into two regions, make the area below the x-axis positive R1R1 N2
[3 marks]
Question
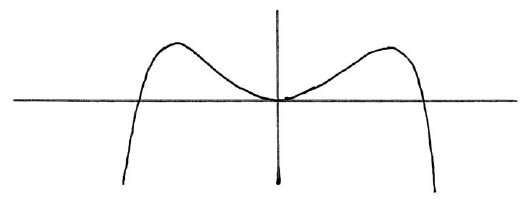
Consider \(f(x) = x\ln (4 – {x^2})\) , for \( – 2 < x < 2\) . The graph of f is given below.
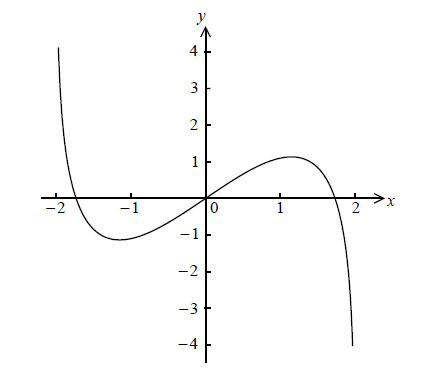
Let P and Q be points on the curve of f where the tangent to the graph of f is parallel to the x-axis.
(i) Find the x-coordinate of P and of Q.
(ii) Consider \(f(x) = k\) . Write down all values of k for which there are exactly two solutions.
Let \(g(x) = {x^3}\ln (4 – {x^2})\) , for \( – 2 < x < 2\) .
Show that \(g'(x) = \frac{{ – 2{x^4}}}{{4 – {x^2}}} + 3{x^2}\ln (4 – {x^2})\) .
Let \(g(x) = {x^3}\ln (4 – {x^2})\) , for \( – 2 < x < 2\) .
Sketch the graph of \(g’\) .
Let \(g(x) = {x^3}\ln (4 – {x^2})\) , for \( – 2 < x < 2\) .
Consider \(g'(x) = w\) . Write down all values of w for which there are exactly two solutions.
Answer/Explanation
Markscheme
(i) \( – 1.15{\text{, }}1.15\) A1A1 N2
(ii) recognizing that it occurs at P and Q (M1)
e.g. \(x = – 1.15\) , \(x = 1.15\)
\(k = – 1.13\) , \(k = 1.13\) A1A1 N3
[5 marks]
evidence of choosing the product rule (M1)
e.g. \(uv’ + vu’\)
derivative of \({x^3}\) is \(3{x^2}\) (A1)
derivative of \(\ln (4 – {x^2})\) is \(\frac{{ – 2x}}{{4 – {x^2}}}\) (A1)
correct substitution A1
e.g. \({x^3} \times \frac{{ – 2x}}{{4 – {x^2}}} + \ln (4 – {x^2}) \times 3{x^2}\)
\(g'(x) = \frac{{ – 2{x^4}}}{{4 – {x^2}}} + 3{x^2}\ln (4 – {x^2})\) AG N0
[4 marks]
A1A1 N2
[2 marks]
\(w = 2.69\) , \(w < 0\) A1A2 N2
[3 marks]
Question
Let \(f'(x) = – 24{x^3} + 9{x^2} + 3x + 1\) .
There are two points of inflexion on the graph of f . Write down the x-coordinates of these points.
Let \(g(x) = f”(x)\) . Explain why the graph of g has no points of inflexion.
Answer/Explanation
Markscheme
valid approach R1
e.g. \(f”(x) = 0\) , the max and min of \(f’\) gives the points of inflexion on f
\( – 0.114{\text{, }}0.364\) (accept (\( – 0.114{\text{, }}0.811\)) and (\(0.364{\text{, }}2.13)\)) A1A1 N1N1
[3 marks]
METHOD 1
graph of g is a quadratic function R1 N1
a quadratic function does not have any points of inflexion R1 N1
METHOD 2
graph of g is concave down over entire domain R1 N1
therefore no change in concavity R1 N1
METHOD 3
\(g”(x) = – 144\) R1 N1
therefore no points of inflexion as \(g”(x) \ne 0\) R1 N1
[2 marks]
Question
Let \(f(x) = x\ln (4 – {x^2})\) , for \( – 2 < x < 2\) . The graph of f is shown below.
The graph of f crosses the x-axis at \(x = a\) , \(x = 0\) and \(x = b\) .
Find the value of a and of b .
The graph of f has a maximum value when \(x = c\) .
Find the value of c .
The region under the graph of f from \(x = 0\) to \(x = c\) is rotated \({360^ \circ }\) about the x-axis. Find the volume of the solid formed.
Let R be the region enclosed by the curve, the x-axis and the line \(x = c\) , between \(x = a\) and \(x = c\) .
Find the area of R .
Answer/Explanation
Markscheme
evidence of valid approach (M1)
e.g. \(f(x) = 0\) , graph
\(a = – 1.73\) , \(b = 1.73\) \((a = – \sqrt 3 {\text{, }}b = \sqrt 3 )\) A1A1 N3
[3 marks]
attempt to find max (M1)
e.g. setting \(f'(x) = 0\) , graph
\(c = 1.15\) (accept (1.15, 1.13)) A1 N2
[2 marks]
attempt to substitute either limits or the function into formula M1
e.g. \(V = \pi {\int_0^c {\left[ {f(x)} \right]} ^2}{\rm{d}}x\) , \(\pi {\int {\left[ {x\ln (4 – {x^2})} \right]} ^2}\) , \(\pi \int_0^{1.149 \ldots } {{y^2}{\rm{d}}x} \)
\(V = 2.16\) A2 N2
[3 marks]
valid approach recognizing 2 regions (M1)
e.g. finding 2 areas
correct working (A1)
e.g. \(\int_0^{ – 1.73 \ldots } {f(x){\rm{d}}x + } \int_0^{1.149 \ldots } {f(x){\rm{d}}x} \) , \( – \int_{ – 1.73 \ldots }^0 {f(x){\rm{d}}x + } \int_0^{1.149 \ldots } {f(x){\rm{d}}x} \)
area \( = 2.07\) (accept 2.06) A2 N3
[4 marks]
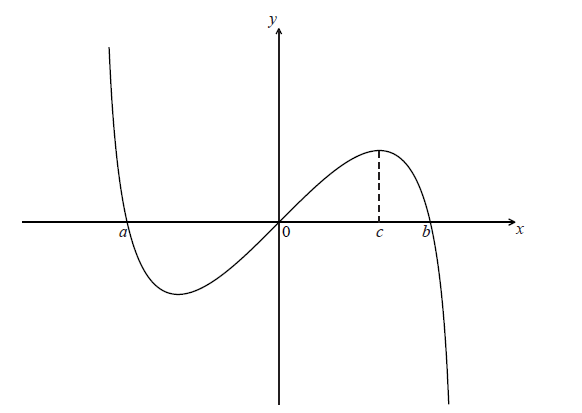
Question
Let \(f(x) = a{x^3} + b{x^2} + c\) , where a , b and c are real numbers. The graph of f passes through the point (2, 9) .
Show that \(8a + 4b + c = 9\) .
The graph of f has a local minimum at \((1{\text{, }}4)\) .
Find two other equations in a , b and c , giving your answers in a similar form to part (a).
Find the value of a , of b and of c .
Answer/Explanation
Markscheme
attempt to substitute coordinates in f (M1)
e.g. \(f(2) = 9\)
correct substitution A1
e.g. \(a \times {2^3} + b \times {2^2} + c = 9\)
\(8a + 4b + c = 9\) AG N0
[2 marks]
recognizing that \((1{\text{, }}4)\) is on the graph of f (M1)
e.g. \(f(1) = 4\)
correct equation A1
e.g. \(a + b + c = 4\)
recognizing that \(f’ = 0\) at minimum (seen anywhere) (M1)
e.g. \(f'(1) = 0\)
\(f'(x) = 3a{x^2} + 2bx\) (seen anywhere) A1A1
correct substitution into derivative (A1)
e.g. \(3a \times {1^2} + 2b \times 1 = 0\)
correct simplified equation A1
e.g. \(3a + 2b = 0\)
[7 marks]
valid method for solving system of equations (M1)
e.g. inverse of a matrix, substitution
\(a = 2\) , \(b = – 3\) , \(c = 5\) A1A1A1 N4
[4 marks]
Question
Let \(f(x) = {x^3} – 2x – 4\) . The following diagram shows part of the curve of f .
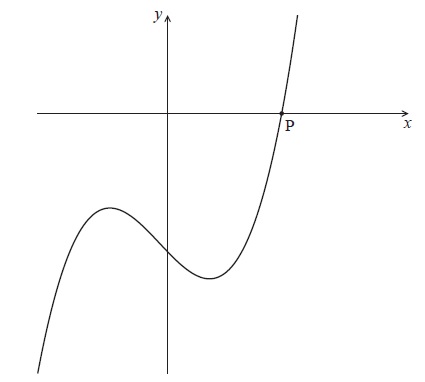
The curve crosses the x-axis at the point P.
Write down the x-coordinate of P.
Write down the gradient of the curve at P.
Find the equation of the normal to the curve at P, giving your equation in the form \(y = ax + b\) .
Answer/Explanation
Markscheme
\(x = 2\) (accept \((2{\text{, }}0)\)) A1 N1
[1 mark]
evidence of finding gradient of f at \(x = 2\) (M1)
e.g. \(f'(2)\)
the gradient is 10 A1 N2
[2 marks]
evidence of negative reciprocal of gradient (M1)
e.g. \(\frac{{ – 1}}{{f'(x)}}\) , \( – \frac{1}{{10}}\)
evidence of correct substitution into equation of a line (A1)
e.g. \(y – 0 = \frac{{ – 1}}{{10}}(x – 2)\) , \(0 = – 0.1(2) + b\)
\(y = – \frac{1}{{10}}x + \frac{2}{{10}}\) (accept \(a = – 0.1\) , \(b = 0.2\) ) A1 N2
[3 marks]
Question
Let \(f(x) = a\cos (b(x – c))\) . The diagram below shows part of the graph of f , for \(0 \le x \le 10\) .
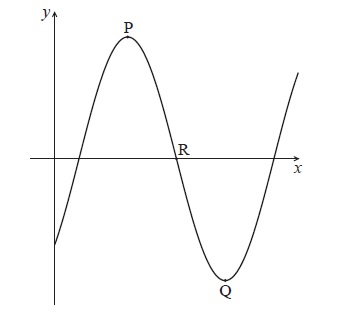
The graph has a local maximum at P(3, 5) , a local minimum at Q(7, − 5) , and crosses the x-axis at R.
Write down the value of
(i) \(a\) ;
(ii) \(c\) .
Find the value of b .
Find the x-coordinate of R.
Answer/Explanation
Markscheme
(i) \(a = 5\) (accept \( – 5\) ) A1 N1
(ii) \(c = 3\) (accept \(c = 7\) , if \(a = – 5\) ) A1 N1
Note: Accept other correct values of c, such as 11, \( – 5\), etc.
[2 marks]
attempt to find period (M1)
e.g. 8 , \(b = \frac{{2\pi }}{{{\rm{period}}}}\)
\(0.785398 \ldots \)
\(b = \frac{{2\pi }}{8}\) (exact), \(\frac{\pi }{4}\) , 0.785 [\(0.785{\text{, }}0.786\)] (do not accept 45) A1 N2
[2 marks]
valid approach (M1)
e.g. \(f(x) = 0\) , symmetry of curve
\(x = 5\) (accept \((5{\text{ ,}}0))\) A1 N2
[2 marks]
Question
The velocity of a particle in ms−1 is given by \(v = {{\rm{e}}^{\sin t}} – 1\) , for \(0 \le t \le 5\) .
On the grid below, sketch the graph of \(v\) .
Find the total distance travelled by the particle in the first five seconds.
Write down the positive \(t\)-intercept.
Answer/Explanation
Markscheme
A1A1A1 N3
Note: Award A1 for approximately correct shape crossing x-axis with \(3 < x < 3.5\) .
Only if this A1 is awarded, award the following:
A1 for maximum in circle, A1 for endpoints in circle.
[3 marks]
\(t = \pi \) (exact), \(3.14\) A1 N1
[1 mark]
recognizing distance is area under velocity curve (M1)
eg \(s = \int v \) , shading on diagram, attempt to integrate
valid approach to find the total area (M1)
eg \({\text{area A}} + {\text{area B}}\) , \(\int {v{\rm{d}}t – \int {v{\rm{d}}t} } \) , \(\int_0^{3.14} {v{\rm{d}}t + } \int_{3.14}^5 {v{\rm{d}}t} \) , \(\int {\left| v \right|} \)
correct working with integration and limits (accept \({\rm{d}}x\) or missing \({\rm{d}}t\) ) (A1)
eg \(\int_0^{3.14} {v{\rm{d}}t + } \int_5^{3.14} {v{\rm{d}}t} \) , \(3.067 \ldots + 0.878 \ldots \) , \(\int_0^5 {\left| {{{\rm{e}}^{\sin t}} – 1} \right|} \)
distance \( = 3.95\) (m) A1 N3
[4 marks]
Question
Let \(f(x) = 5 – {x^2}\). Part of the graph of \(f\)is shown in the following diagram.
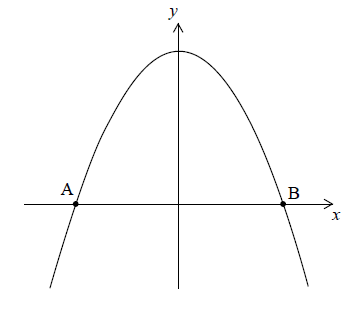
The graph crosses the \(x\)-axis at the points \(\rm{A}\) and \(\rm{B}\).
Find the \(x\)-coordinate of \({\text{A}}\) and of \({\text{B}}\).
The region enclosed by the graph of \(f\) and the \(x\)-axis is revolved \(360^\circ \) about the \(x\)-axis.
Find the volume of the solid formed.
Answer/Explanation
Markscheme
recognizing \(f(x) = 0\) (M1)
eg \(f = 0,{\text{ }}{x^2} = 5\)
\(x = \pm 2.23606\)
\(x = \pm \sqrt 5 {\text{ (exact), }}x = \pm 2.24\) A1A1 N3
[3 marks]
attempt to substitute either limits or the function into formula
involving \({f^2}\) (M1)
eg \(\pi \int {{{\left( {5 – {x^2}} \right)}^2}{\text{d}}x,{\text{ }}\pi \int_{ – 2.24}^{2.24} {\left( {{x^4} – 10{x^2} + 25} \right)} ,{\text{ }}2\pi \int_0^{\sqrt 5 } {{f^2}} } \)
\(187.328\)
volume \(= 187\) A2 N3
[3 marks]
Question
Let \(f(x) = \frac{{2x – 6}}{{1 – x}}\), for \(x \ne 1\).
For the graph of \(f\)
(i) find the \(x\)-intercept;
(ii) write down the equation of the vertical asymptote;
(iii) find the equation of the horizontal asymptote.
Find \(\mathop {\lim }\limits_{x \to \infty } f(x)\).
Answer/Explanation
Markscheme
(i) valid approach (M1)
eg\(\;\;\;\)sketch, \(f(x) = 0,{\text{ }}0 = 2x – 6\)
\(x = 3\) or \((3,{\text{ }}0)\) A1 N2
(ii) \(x = 1\;\;\;\)(must be equation) A1 N1
(iii) valid approach (M1)
eg\(\;\;\;\)sketch, \(\frac{{2x}}{{ – 1x}}\), inputting large values of \(x\), L’Hopital’s rule
\(y = – 2\;\;\;\)(must be equation) A1 N2
[5 marks]
valid approach (M1)
eg\(\;\;\;\)recognizing that \(\mathop {\lim }\limits_{x \to \infty } \) is related to the horizontal asymptote, table with large values of \(x\), their \(y\) value from (a)(iii), L’Hopital’s rule
\(\mathop {\lim }\limits_{x \to \infty } f(x) = – 2\) A1 N2
[2 marks]
Total [7 marks]
Question
The following diagram shows part of the graph of \(f(x) = – 2{x^3} + 5.1{x^2} + 3.6x – 0.4\).
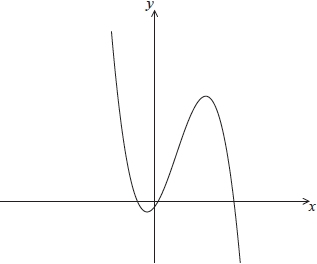
Find the coordinates of the local minimum point.
The graph of \(f\) is translated to the graph of \(g\) by the vector \(\left( {\begin{array}{*{20}{c}} 0 \\ k \end{array}} \right)\). Find all values of \(k\) so that \(g(x) = 0\) has exactly one solution.
Answer/Explanation
Markscheme
\(( – 0.3,{\text{ }} – 0.967)\)
\(x = – 0.3\) (exact), \(y = – 0.967\) (exact) A1A1 N2
[2 marks]
\(y\)-coordinate of local maximum is \(y = 11.2\) (A1)
negating the \(y\)-coordinate of one of the max/min (M1)
eg\(\;\;\;y = 0.967,{\text{ }}y = – 11.2\)
recognizing that the solution set has two intervals R1
eg\(\;\;\;\)two answers,
\(k < – 11.2,{\text{ }}k > 0.967\) A1A1 N3N2
[5 marks]
Notes: If working shown, do not award the final mark if strict inequalities are not used.
If no working shown, award N2 for \(k \le – 11.2\) or N1 for \(k \ge 0.967\)
Total [7 marks]
Question
Consider a function \(f\), for \(0 \le x \le 10\). The following diagram shows the graph of \(f’\), the derivative of \(f\).
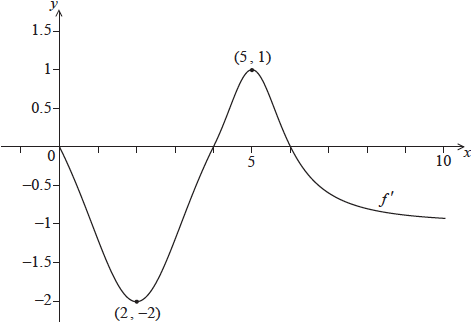
The graph of \(f’\) passes through \((2,{\text{ }} – 2)\) and \((5,{\text{ }}1)\), and has \(x\)-intercepts at \(0\), \(4\) and \(6\).
The graph of \(f\) has a local maximum point when \(x = p\). State the value of \(p\), and justify your answer.
Write down \(f'(2)\).
Let \(g(x) = \ln \left( {f(x)} \right)\) and \(f(2) = 3\).
Find \(g'(2)\).
Verify that \(\ln 3 + \int_2^a {g'(x){\text{d}}x = g(a)} \), where \(0 \le a \le 10\).
The following diagram shows the graph of \(g’\), the derivative of \(g\).
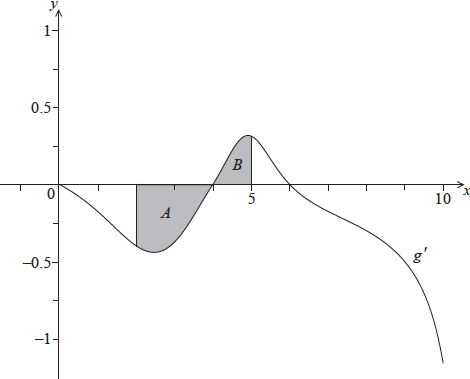
The shaded region \(A\) is enclosed by the curve, the \(x\)-axis and the line \(x = 2\), and has area \({\text{0.66 unit}}{{\text{s}}^{\text{2}}}\).
The shaded region \(B\) is enclosed by the curve, the \(x\)-axis and the line \(x = 5\), and has area \({\text{0.21 unit}}{{\text{s}}^{\text{2}}}\).
Find \(g(5)\).
Answer/Explanation
Markscheme
\(p = 6\) A1 N1
recognizing that turning points occur when \(f'(x) = 0\) R1 N1
eg\(\;\;\;\)correct sign diagram
\(f’\) changes from positive to negative at \(x = 6\) R1 N1
[3 marks]
\(f'(2) = – 2\) A1 N1
[1 mark]
attempt to apply chain rule (M1)
eg\(\;\;\;\ln (x)’ \times f'(x)\)
correct expression for \(g'(x)\) (A1)
eg\(\;\;\;g'(x) = \frac{1}{{f(x)}} \times f'(x)\)
substituting \(x = 2\) into their \(g’\) (M1)
eg\(\;\;\;\frac{{f'(2)}}{{f(2)}}\)
\( – 0.666667\)
\(g'(2) = – \frac{2}{3}{\text{ (exact), }} – 0.667\) A1 N3
[4 marks]
evidence of integrating \(g'(x)\) (M1)
eg\(\;\;\;g(x)|_2^a,{\text{ }}g(x)|_a^2\)
applying the fundamental theorem of calculus (seen anywhere) R1
eg\(\;\;\;\int_2^a {g'(x) = g(a) – g(2)} \)
correct substitution into integral (A1)
eg\(\;\;\;\ln 3 + g(a) – g(2),{\text{ }}\ln 3 + g(a) – \ln \left( {f(2)} \right)\)
\(\ln 3 + g(a) – \ln 3\) A1
\(\ln 3 + \int_2^a {g'(x) = g(a)} \) AG N0
[4 marks]
METHOD 1
substituting \(a = 5\) into the formula for \(g(a)\) (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x,{\text{ }}g(5) = \ln 3 + \int_2^5 {g'(x){\text{d}}x\;\;\;} } \left( {{\text{do not accept only }}g(5)} \right)\)
attempt to substitute areas (M1)
eg\(\;\;\;\ln 3 + 0.66 – 0.21,{\text{ }}\ln 3 + 0.66 + 0.21\)
correct working
eg\(\;\;\;g(5) = \ln 3 + ( – 0.66 + 0.21)\) (A1)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 2
attempt to set up an equation for one shaded region (M1)
eg\(\;\;\;\int_4^5 {g'(x){\text{d}}x = 0.21,{\text{ }}\int_2^4 {g'(x){\text{d}}x = – 0.66,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } } \)
two correct equations (A1)
eg\(\;\;\;g(5) – g(4) = 0.21,{\text{ }}g(2) – g(4) = 0.66\)
combining equations to eliminate \(g(4)\) (M1)
eg\(\;\;\;g(5) – [\ln 3 – 0.66] = 0.21\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 3
attempt to set up a definite integral (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x = – 0.66 + 0.21,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } \)
correct working (A1)
eg\(\;\;\;g(5) – g(2) = – 0.45\)
correct substitution (A1)
eg\(\;\;\;g(5) – \ln 3 = – 0.45\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
[4 marks]
Total [16 marks]
Question
Let \(f(x) = k{x^2} + kx\) and \(g(x) = x – 0.8\). The graphs of \(f\) and \(g\) intersect at two distinct points.
Find the possible values of \(k\).
Answer/Explanation
Markscheme
attempt to set up equation (M1)
eg\(\;\;\;f = g,{\text{ }}k{x^2} + kx = x – 0.8\)
rearranging their equation to equal zero M1
eg\(\;\;\;k{x^2} + kx – x + 0.8 = 0,{\text{ }}k{x^2} + x(k – 1) + 0.8 = 0\)
evidence of discriminant (if seen explicitly, not just in quadratic formula) (M1)
eg\(\;\;\;{b^2} – 4ac,{\text{ }}\Delta = {(k – 1)^2} – 4k \times 0.8,{\text{ }}D = 0\)
correct discriminant (A1)
eg\(\;\;\;{(k – 1)^2} – 4k \times 0.8,{\text{ }}{k^2} – 5.2k + 1\)
evidence of correct discriminant greater than zero R1
eg\(\;\;\;{k^2} – 5.2k + 1 > 0,{\text{ }}{(k – 1)^2} – 4k \times 0.8 > 0\), correct answer
both correct values (A1)
eg\(\;\;\;0.2,{\text{ }}5\)
correct answer A2 N3
eg\(\;\;\;k < 0.2,{\text{ }}k \ne 0,{\text{ }}k > 5\)
[8 marks]
Question
Let \(f(x) = 2\ln (x – 3)\), for \(x > 3\). The following diagram shows part of the graph of \(f\).
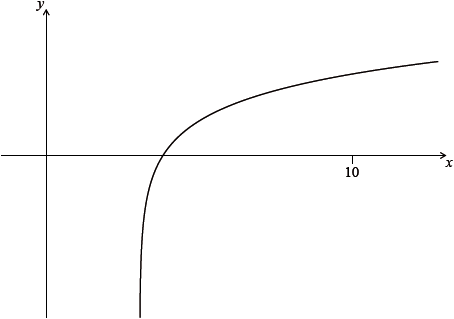
Find the equation of the vertical asymptote to the graph of \(f\).
Find the \(x\)-intercept of the graph of \(f\).
The region enclosed by the graph of \(f\), the \(x\)-axis and the line \(x = 10\) is rotated \(360\)° about the \(x\)-axis. Find the volume of the solid formed.
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\;\;\;\)horizontal translation \(3\) units to the right
\(x = 3\) (must be an equation) A1 N2
[2 marks]
valid approach (M1)
eg\(\;\;\;f(x) = 0,{\text{ }}{e^0} = x – 3\)
\(4,{\text{ }}x = 4,{\text{ }}(4,{\text{ }}0)\) A1 N2
[2 marks]
attempt to substitute either their correct limits or the function into formula involving \({f^2}\) (M1)
eg\(\;\;\;\int_4^{10} {{f^2},{\text{ }}\pi \int {{{\left( {2\ln (x – 3)} \right)}^2}{\text{d}}x} } \)
\(141.537\)
volume = \(142\) A2 N3
[3 marks]
Total [7 marks]
Question
A particle P moves along a straight line so that its velocity, \(v\,{\text{m}}{{\text{s}}^{ – 1}}\), after \(t\) seconds, is given by \(v = \cos 3t – 2\sin t – 0.5\), for \(0 \leqslant t \leqslant 5\). The initial displacement of P from a fixed point O is 4 metres.
The following sketch shows the graph of \(v\).
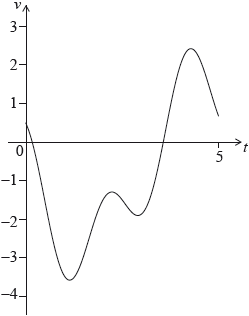
Find the displacement of P from O after 5 seconds.
Find when P is first at rest.
Write down the number of times P changes direction.
Find the acceleration of P after 3 seconds.
Find the maximum speed of P.
Answer/Explanation
Markscheme
METHOD 1
recognizing \(s = \int v \) (M1)
recognizing displacement of P in first 5 seconds (seen anywhere) A1
(accept missing \({\text{d}}t\))
eg\(\,\,\,\,\,\)\(\int_0^5 {v{\text{d}}t,{\text{ }} – 3.71591} \)
valid approach to find total displacement (M1)
eg\(\,\,\,\,\,\)\(4 + ( – 3.7159),{\text{ }}s = 4 + \int_0^5 v \)
0.284086
0.284 (m) A2 N3
METHOD 2
recognizing \(s = \int v \) (M1)
correct integration A1
eg\(\,\,\,\,\,\)\(\frac{1}{3}\sin 3t + 2\cos t – \frac{t}{2} + c\) (do not penalize missing “\(c\)”)
attempt to find \(c\) (M1)
eg\(\,\,\,\,\,\)\(4 = \frac{1}{3}\sin (0) + 2\cos (0)–\frac{0}{2} + c,{\text{ }}4 = \frac{1}{3}\sin 3t + 2\cos t – \frac{t}{2} + c,{\text{ }}2 + c = 4\)
attempt to substitute \(t = 5\) into their expression with \(c\) (M1)
eg\(\,\,\,\,\,\)\(s(5),{\text{ }}\frac{1}{3}\sin (15) + 2\cos (5)5–\frac{5}{2} + 2\)
0.284086
0.284 (m) A1 N3
[5 marks]
recognizing that at rest, \(v = 0\) (M1)
\(t = 0.179900\)
\(t = 0.180{\text{ (secs)}}\) A1 N2
[2 marks]
recognizing when change of direction occurs (M1)
eg\(\,\,\,\,\,\)\(v\) crosses \(t\) axis
2 (times) A1 N2
[2 marks]
acceleration is \({v’}\) (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(v'(3)\)
0.743631
\(0.744{\text{ }}({\text{m}}{{\text{s}}^{ – 2}})\) A1 N2
[2 marks]
valid approach involving max or min of \(v\) (M1)
eg\(\,\,\,\,\,\)\(v\prime = 0,{\text{ }}a = 0\), graph
one correct co-ordinate for min (A1)
eg\(\,\,\,\,\,\)\(1.14102,{\text{ }}-3.27876\)
\(3.28{\text{ }}({\text{m}}{{\text{s}}^{ – 1}})\) A1 N2
[3 marks]
Question
Let \(f(x) = \frac{1}{{x – 1}} + 2\), for \(x > 1\).
Let \(g(x) = a{e^{ – x}} + b\), for \(x \geqslant 1\). The graphs of \(f\) and \(g\) have the same horizontal asymptote.
Write down the equation of the horizontal asymptote of the graph of \(f\).
Find \(f'(x)\).
Write down the value of \(b\).
Given that \(g'(1) = – e\), find the value of \(a\).
There is a value of \(x\), for \(1 < x < 4\), for which the graphs of \(f\) and \(g\) have the same gradient. Find this gradient.
Answer/Explanation
Markscheme
\(y = 2\) (correct equation only) A2 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\({(x – 1)^{ – 1}} + 2,{\text{ }}f'(x) = \frac{{0(x – 1) – 1}}{{{{(x – 1)}^2}}}\)
\( – {(x – 1)^{ – 2}},{\text{ }}f'(x) = \frac{{ – 1}}{{{{(x – 1)}^2}}}\) A1 N2
[2 marks]
correct equation for the asymptote of \(g\)
eg\(\,\,\,\,\,\)\(y = b\) (A1)
\(b = 2\) A1 N2
[2 marks]
correct derivative of g (seen anywhere) (A2)
eg\(\,\,\,\,\,\)\(g'(x) = – a{{\text{e}}^{ – x}}\)
correct equation (A1)
eg\(\,\,\,\,\,\)\( – {\text{e}} = – a{{\text{e}}^{ – 1}}\)
7.38905
\(a = {{\text{e}}^2}{\text{ }}({\text{exact}}),{\text{ }}7.39\) A1 N2
[4 marks]
attempt to equate their derivatives (M1)
eg\(\,\,\,\,\,\)\(f'(x) = g'(x),{\text{ }}\frac{{ – 1}}{{{{(x – 1)}^2}}} = – a{{\text{e}}^{ – x}}\)
valid attempt to solve their equation (M1)
eg\(\,\,\,\,\,\)correct value outside the domain of \(f\) such as 0.522 or 4.51,
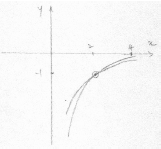
correct solution (may be seen in sketch) (A1)
eg\(\,\,\,\,\,\)\(x = 2,{\text{ }}(2,{\text{ }} – 1)\)
gradient is \( – 1\) A1 N3
[4 marks]
Question
Let \(f(x) = 0.225{x^3} – 2.7x\), for \( – 3 \leqslant x \leqslant 3\). There is a local minimum point at A.
On the following grid,
Find the coordinates of A.
(i) sketch the graph of \(f\), clearly indicating the point A;
(ii) sketch the tangent to the graph of \(f\) at A.
Answer/Explanation
Markscheme
\({\text{A }}(2,{\text{ }}-3.6)\) A1A1 N2
[2 marks]
(i) (ii)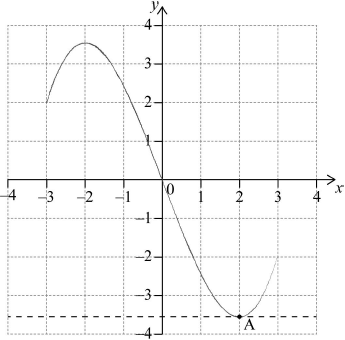 
A1
A1A1A1 N4
A1 N1
Notes: (i) Award A1 for correct cubic shape with correct curvature.
Only if this A1 is awarded, award the following:
A1 for passing through their point A and the origin,
A1 for endpoints,
A1 for maximum.
(ii) Award A1 for horizontal line through their A.
[5 marks]
Question
Let \(f(x) = – 0.5{x^4} + 3{x^2} + 2x\). The following diagram shows part of the graph of \(f\).
There are \(x\)-intercepts at \(x = 0\) and at \(x = p\). There is a maximum at A where \(x = a\), and a point of inflexion at B where \(x = b\).
Find the value of \(p\).
Write down the coordinates of A.
Write down the rate of change of \(f\) at A.
Find the coordinates of B.
Find the the rate of change of \(f\) at B.
Let \(R\) be the region enclosed by the graph of \(f\) , the \(x\)-axis, the line \(x = b\) and the line \(x = a\). The region \(R\) is rotated 360° about the \(x\)-axis. Find the volume of the solid formed.
Answer/Explanation
Markscheme
evidence of valid approach (M1)
eg\(\,\,\,\,\,\)\(f(x) = 0,{\text{ }}y = 0\)
2.73205
\(p = 2.73\) A1 N2
[2 marks]
1.87938, 8.11721
\((1.88,{\text{ }}8.12)\) A2 N2
[2 marks]
rate of change is 0 (do not accept decimals) A1 N1
[1 marks]
METHOD 1 (using GDC)
valid approach M1
eg\(\,\,\,\,\,\)\(f’’ = 0\), max/min on \(f’,{\text{ }}x = – 1\)
sketch of either \(f’\) or \(f’’\), with max/min or root (respectively) (A1)
\(x = 1\) A1 N1
Substituting their \(x\) value into \(f\) (M1)
eg\(\,\,\,\,\,\)\(f(1)\)
\(y = 4.5\) A1 N1
METHOD 2 (analytical)
\(f’’ = – 6{x^2} + 6\) A1
setting \(f’’ = 0\) (M1)
\(x = 1\) A1 N1
substituting their \(x\) value into \(f\) (M1)
eg\(\,\,\,\,\,\)\(f(1)\)
\(y = 4.5\) A1 N1
[4 marks]
recognizing rate of change is \(f’\) (M1)
eg\(\,\,\,\,\,\)\(y’,{\text{ }}f’(1)\)
rate of change is 6 A1 N2
[3 marks]
attempt to substitute either limits or the function into formula (M1)
involving \({f^2}\) (accept absence of \(\pi \) and/or \({\text{d}}x\))
eg\(\,\,\,\,\,\)\(\pi \int {{{( – 0.5{x^4} + 3{x^2} + 2x)}^2}{\text{d}}x,{\text{ }}\int_1^{1.88} {{f^2}} } \)
128.890
\({\text{volume}} = 129\) A2 N3
[3 marks]
Question
Let \(f(x) = \frac{{6{x^2} – 4}}{{{{\text{e}}^x}}}\), for \(0 \leqslant x \leqslant 7\).
Find the \(x\)-intercept of the graph of \(f\).
The graph of \(f\) has a maximum at the point A. Write down the coordinates of A.
On the following grid, sketch the graph of \(f\).
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(f(x) = 0,{\text{ }} \pm 0.816\)
0.816496
\(x = \sqrt {\frac{2}{3}} \) (exact), 0.816 A1 N2
[2 marks]
\((2.29099,{\text{ }}2.78124)\)
\({\text{A}}(2.29,{\text{ }}2.78)\) A1A1 N2
[2 marks]
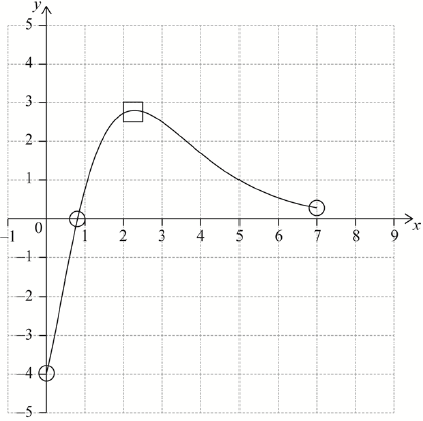A1A1A1 N3
Notes: Award A1 for correct domain and endpoints at \(x = 0\) and \(x = 7\) in circles,
A1 for maximum in square,
A1 for approximately correct shape that passes through their \(x\)-intercept in circle and has changed from concave down to concave up between 2.29 and 7.
[3 marks]
Question
Let g(x) = −(x − 1)2 + 5.
Let f(x) = x2. The following diagram shows part of the graph of f.
The graph of g intersects the graph of f at x = −1 and x = 2.
Write down the coordinates of the vertex of the graph of g.
On the grid above, sketch the graph of g for −2 ≤ x ≤ 4.
Find the area of the region enclosed by the graphs of f and g.
Answer/Explanation
Markscheme
(1,5) (exact) A1 N1
[1 mark]
A1A1A1 N3
Note: The shape must be a concave-down parabola.
Only if the shape is correct, award the following for points in circles:
A1 for vertex,
A1 for correct intersection points,
A1 for correct endpoints.
[3 marks]
integrating and subtracting functions (in any order) (M1)
eg \(\int {f – g} \)
correct substitution of limits or functions (accept missing dx, but do not accept any errors, including extra bits) (A1)
eg \(\int_{ – 1}^2 {g – f,\,\,\int { – {{\left( {x – 1} \right)}^2}} } + 5 – {x^2}\)
area = 9 (exact) A1 N2
[3 marks]
Question
Let \(f\left( x \right) = \,\,{\text{sin}}\,\left( {{e^x}} \right)\) for 0 ≤ \(x\) ≤ 1.5. The following diagram shows the graph of \(f\).
Find the x-intercept of the graph of \(f\).
The region enclosed by the graph of \(f\), the y-axis and the x-axis is rotated 360° about the x-axis.
Find the volume of the solid formed.
Answer/Explanation
Markscheme
valid approach (M1)
eg \(f\left( x \right) = 0,\,\,\,\,{e^x} = 180\) or 0…
1.14472
\(x = {\text{ln}}\,\pi \) (exact), 1.14 A1 N2
[2 marks]
attempt to substitute either their limits or the function into formula involving \({f^2}\). (M1)
eg \({\int_0^{1.14} {{f^2},\,\,\pi \int {\left( {{\text{sin}}\,\left( {{e^x}} \right)} \right)} } ^2}dx,\,\,0.795135\)
2.49799
volume = 2.50 A2 N3
[3 marks]
Question
Let \(f\left( x \right) = \frac{{8x – 5}}{{cx + 6}}\) for \(x \ne – \frac{6}{c},\,\,c \ne 0\).
The line x = 3 is a vertical asymptote to the graph of f. Find the value of c.
Write down the equation of the horizontal asymptote to the graph of f.
The line y = k, where \(k \in \mathbb{R}\) intersects the graph of \(\left| {f\left( x \right)} \right|\) at exactly one point. Find the possible values of k.
Answer/Explanation
Markscheme
valid approach (M1)
eg \(cx + 6 = 0,\,\, – \frac{6}{c} = 3\)
c = −2 A1 N2
[2 marks]
valid approach (M1)
eg \(\mathop {{\text{lim}}\,f}\limits_{x \to \infty } \left( x \right),\,\,y = \frac{8}{c}\)
y = −4 (must be an equation) A1 N2
[2 marks]
valid approach to analyze modulus function (M1)
eg sketch, horizontal asymptote at y = 4, y = 0
k = 4, k = 0 A2 N3
[3 marks]
Question
Let \(f(x) = 4x – {{\rm{e}}^{x – 2}} – 3\) , for \(0 \le x \le 5\) .
Find the x-intercepts of the graph of f .
On the grid below, sketch the graph of f .
Write down the gradient of the graph of f at \(x = 3\) .
Answer/Explanation
Markscheme
intercepts when \(f(x) = 0\) M1
(0.827, 0) (4.78, 0) (accept \(x = 0.827\), \(x = 4.78\) ) A1A1 N3
[3 marks]
A1A1A1 N3
Note: Award A1 for maximum point in circle, A1 for x-intercepts in circles, A1 for correct shape (y approximately greater than \( – 3.14\)).
[3 marks]
gradient is 1.28 A1 N1
[1 mark]