Question
The graph of \(y = f(x){\text{ for }} – 2 \leqslant x \leqslant 8\) is shown.
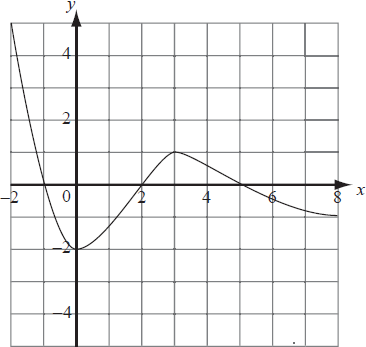
On the set of axes provided, sketch the graph of \(y = \frac{1}{{f(x)}}\), clearly showing any asymptotes and indicating the coordinates of any local maxima or minima.
▶️Answer/Explanation
Markscheme
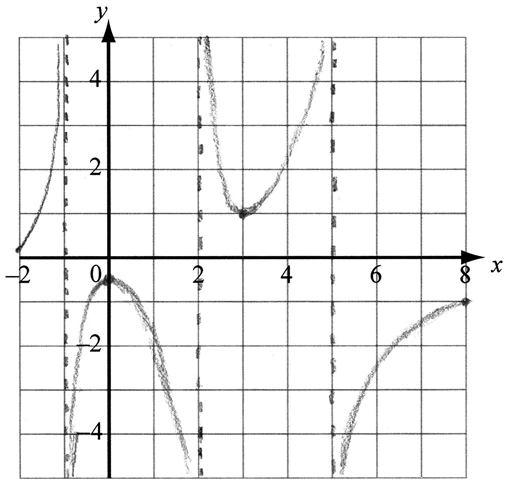A1A1A1A1A1
Notes: Award A1 for vertical asymptotes at x = −1, x = 2 and x = 5 .
A1 for \(x \to – 2,{\text{ }}\frac{1}{{f(x)}} \to {0^ + }\)
A1 for \(x \to 8,{\text{ }}\frac{1}{{f(x)}} \to – 1\)
A1 for local maximum at \(\left( {0, – \frac{1}{2}} \right)\) (branch containing local max. must be present)
A1 for local minimum at (3, 1) (branch containing local min. must be present)
In each branch, correct asymptotic behaviour must be displayed to obtain the A1.
Disregard any stated horizontal asymptotes such as y = 0 or y = −1 .
[5 marks]
Question
The function \(f\) is given by \(f(x) = \frac{{3{x^2} + 10}}{{{x^{\text{2}}} – 4}},{\text{ }}x \in \mathbb{R},{\text{ }}x \ne 2,{\text{ }}x \ne – 2\).
a.Prove that \(f\) is an even function.[2]
b.i.Sketch the graph \(y = f(x)\).[3]
b.ii.Write down the range of \(f\).[2]
▶️Answer/Explanation
Markscheme
\(f( – x) = \frac{{3{{( – x)}^2} + 10}}{{{{( – x)}^2} – 4}}\) A1
\( = \frac{{3{x^2} + 10}}{{{x^2} – 4}} = f(x)\)
\(f(x) = f( – x)\) R1
hence this is an even function AG
Note: Award A1R1 for the statement, all the powers are even hence \(f(x) = f( – x)\).
Note: Just stating all the powers are even is A0R0.
Note: Do not accept arguments based on the symmetry of the graph.
[2 marks]
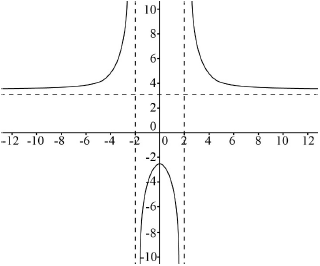
correct shape in 3 parts which are asymptotic and symmetrical A1
correct vertical asymptotes clear at 2 and –2 A1
correct horizontal asymptote clear at 3 A1
[3 marks]
\(f(x) > 3\) A1
\(f(x) \leqslant – 2.5\) A1
[2 marks]
Question
Consider the expression \(f\left( x \right) = {\text{tan}}\left( {x + \frac{\pi }{4}} \right){\text{cot}}\left( {\frac{\pi }{4} – x} \right)\).
The expression \(f\left( x \right)\) can be written as \(g\left( t \right)\) where \(t = {\text{tan}}\,x\).
Let \(\alpha \), β be the roots of \(g\left( t \right) = k\), where 0 < \(k\) < 1.
a.i.Sketch the graph of \(y = f\left( x \right)\) for \( – \frac{{5\pi }}{8} \leqslant x \leqslant \frac{\pi }{8}\).[2]
a.ii.With reference to your graph, explain why \(f\) is a function on the given domain.[1]
a.iii.Explain why \(f\) has no inverse on the given domain.[1]
a.iv.Explain why \(f\) is not a function for \( – \frac{{3\pi }}{4} \leqslant x \leqslant \frac{\pi }{4}\).[1]
b.Show that \(g\left( t \right) = {\left( {\frac{{1 + t}}{{1 – t}}} \right)^2}\).[3]
c.Sketch the graph of \(y = g\left( t \right)\) for t ≤ 0. Give the coordinates of any intercepts and the equations of any asymptotes.[3]
d.i.Find \(\alpha \) and β in terms of \(k\).[5]
d.ii.Show that \(\alpha \) + β < −2.[2]
▶️Answer/Explanation
Markscheme
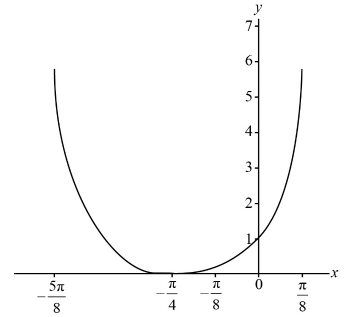A1A1
A1 for correct concavity, many to one graph, symmetrical about the midpoint of the domain and with two axes intercepts.
Note: Axes intercepts and scales not required.
A1 for correct domain
[2 marks]
for each value of \(x\) there is a unique value of \(f\left( x \right)\) A1
Note: Accept “passes the vertical line test” or equivalent.
[1 mark]
no inverse because the function fails the horizontal line test or equivalent R1
Note: No FT if the graph is in degrees (one-to-one).
[1 mark]
the expression is not valid at either of \(x = \frac{\pi }{4}\,\,\left( {{\text{or}} – \frac{{3\pi }}{4}} \right)\) R1
[1 mark]
METHOD 1
\(f\left( x \right) = \frac{{{\text{tan}}\left( {x + \frac{\pi }{4}} \right)}}{{{\text{tan}}\left( {\frac{\pi }{4} – x} \right)}}\) M1
\( = \frac{{\frac{{{\text{tan}}\,x + {\text{tan}}\,\frac{\pi }{4}}}{{1 – {\text{tan}}\,x\,{\text{tan}}\,\frac{\pi }{4}}}}}{{\frac{{{\text{tan}}\,\frac{\pi }{4} – {\text{tan}}\,x}}{{1 + {\text{tan}}\,\frac{\pi }{4}{\text{tan}}\,x}}}}\) M1A1
\( = {\left( {\frac{{1 + t}}{{1 – t}}} \right)^2}\) AG
METHOD 2
\(f\left( x \right) = {\text{tan}}\left( {x + \frac{\pi }{4}} \right){\text{tan}}\left( {\frac{\pi }{2} – \frac{\pi }{4} + x} \right)\) (M1)
\( = {\text{ta}}{{\text{n}}^2}\left( {x + \frac{\pi }{4}} \right)\) A1
\(g\left( t \right) = {\left( {\frac{{{\text{tan}}\,x + {\text{tan}}\,\frac{\pi }{4}}}{{1 – {\text{tan}}\,x\,{\text{tan}}\,\frac{\pi }{4}}}} \right)^2}\) A1
\( = {\left( {\frac{{1 + t}}{{1 – t}}} \right)^2}\) AG
[3 marks]
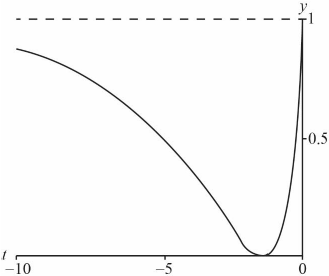
for t ≤ 0, correct concavity with two axes intercepts and with asymptote \(y\) = 1 A1
t intercept at (−1, 0) A1
\(y\) intercept at (0, 1) A1
[3 marks]
METHOD 1
\(\alpha \), β satisfy \(\frac{{{{\left( {1 + t} \right)}^2}}}{{{{\left( {1 – t} \right)}^2}}} = k\) M1
\(1 + {t^2} + 2t = k\left( {1 + {t^2} – 2t} \right)\) A1
\(\left( {k – 1} \right){t^2} – 2\left( {k + 1} \right)t + \left( {k – 1} \right) = 0\) A1
attempt at using quadratic formula M1
\(\alpha \), β \( = \frac{{k + 1 \pm 2\sqrt k }}{{k – 1}}\) or equivalent A1
METHOD 2
\(\alpha \), β satisfy \(\frac{{1 + t}}{{1 – t}} = \left( \pm \right)\sqrt k \) M1
\(t + \sqrt k t = \sqrt k – 1\) M1
\(t = \frac{{\sqrt k – 1}}{{\sqrt k + 1}}\) (or equivalent) A1
\(t – \sqrt k t = – \left( {\sqrt k + 1} \right)\) M1
\(t = \frac{{\sqrt k + 1}}{{\sqrt k – 1}}\) (or equivalent) A1
so for eg, \(\alpha = \frac{{\sqrt k – 1}}{{\sqrt k + 1}}\), β \( = \frac{{\sqrt k + 1}}{{\sqrt k – 1}}\)
[5 marks]
\(\alpha \) + β \( = 2\frac{{\left( {k + 1} \right)}}{{\left( {k – 1} \right)}}\,\left( { = – 2\frac{{\left( {1 + k} \right)}}{{\left( {1 – k} \right)}}} \right)\) A1
since \(1 + k > 1 – k\) R1
\(\alpha \) + β < −2 AG
Note: Accept a valid graphical reasoning.
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]