Download IITian Academy App for accessing Online Mock Tests and More..
Question
Let \(f(x) = {x^2}\) and \(g(x) = 2{(x – 1)^2}\) .
The graph of g can be obtained from the graph of f using two transformations.
Give a full geometric description of each of the two transformations.
The graph of g is translated by the vector \(\left( {\begin{array}{*{20}{c}}
3\\
{ – 2}
\end{array}} \right)\) to give the graph of h.
The point \(( – 1{\text{, }}1)\) on the graph of f is translated to the point P on the graph of h.
Find the coordinates of P.
Answer/Explanation
Markscheme
in any order
translated 1 unit to the right A1 N1
stretched vertically by factor 2 A1 N1
[2 marks]
METHOD 1
finding coordinates of image on g (A1)(A1)
e.g. \( – 1 + 1 = 0\) , \(1 \times 2 = 2\) , \(( – 1{\text{, }}1) \to ( – 1 + 1{\text{, }}2 \times 1)\) , \((0{\text{, }}2)\)
P is (3, 0) A1A1 N4
METHOD 2
\(h(x) = 2{(x – 4)^2} – 2\) (A1)(A1)
P is \((3{\text{, }}0)\) A1A1 N4
Question
Let \(f(x) = \frac{{ax}}{{{x^2} + 1}}\) , \( – 8 \le x \le 8\) , \(a \in \mathbb{R}\) .The graph of f is shown below.
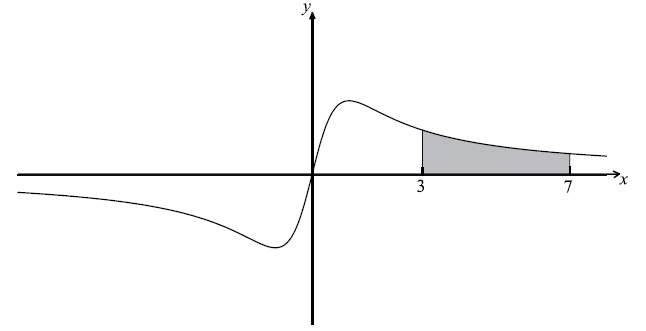
The region between \(x = 3\) and \(x = 7\) is shaded.
Show that \(f( – x) = – f(x)\) .
Given that \(f”(x) = \frac{{2ax({x^2} – 3)}}{{{{({x^2} + 1)}^3}}}\) , find the coordinates of all points of inflexion.
It is given that \(\int {f(x){\rm{d}}x = \frac{a}{2}} \ln ({x^2} + 1) + C\) .
(i) Find the area of the shaded region, giving your answer in the form \(p\ln q\) .
(ii) Find the value of \(\int_4^8 {2f(x – 1){\rm{d}}x} \) .
Answer/Explanation
Markscheme
METHOD 1
evidence of substituting \( – x\) for \(x\) (M1)
\(f( – x) = \frac{{a( – x)}}{{{{( – x)}^2} + 1}}\) A1
\(f( – x) = \frac{{ – ax}}{{{x^2} + 1}}\) \(( = – f(x))\) AG N0
METHOD 2
\(y = – f(x)\) is reflection of \(y = f(x)\) in x axis
and \(y = f( – x)\) is reflection of \(y = f(x)\) in y axis (M1)
sketch showing these are the same A1
\(f( – x) = \frac{{ – ax}}{{{x^2} + 1}}\) \(( = – f(x))\) AG N0
[2 marks]
evidence of appropriate approach (M1)
e.g. \(f”(x) = 0\)
to set the numerator equal to 0 (A1)
e.g. \(2ax({x^2} – 3) = 0\) ; \(({x^2} – 3) = 0\)
(0, 0) , \(\left( {\sqrt 3 ,\frac{{a\sqrt 3 }}{4}} \right)\) , \(\left( { – \sqrt 3 , – \frac{{a\sqrt 3 }}{4}} \right)\) (accept \(x = 0\) , \(y = 0\) etc) A1A1A1A1A1 N5
[7 marks]
(i) correct expression A2
e.g. \(\left[ {\frac{a}{2}\ln ({x^2} + 1)} \right]_3^7\) , \(\frac{a}{2}\ln 50 – \frac{a}{2}\ln 10\) , \(\frac{a}{2}(\ln 50 – \ln 10)\)
area = \(\frac{a}{2}\ln 5\) A1A1 N2
(ii) METHOD 1
recognizing the shift that does not change the area (M1)
e.g. \(\int_4^8 {f(x – 1){\rm{d}}x} = \int_3^7 {f(x){\rm{d}}x} \) , \(\frac{a}{2}\ln 5\)
recognizing that the factor of 2 doubles the area (M1)
e.g. \(\int_4^8 {2f(x – 1){\rm{d}}x = } 2\int_4^8 {f(x – 1){\rm{d}}x} \) \(\left( { = 2\int_3^7 {f(x){\rm{d}}x} } \right)\)
\(\int_4^8 {2f(x – 1){\rm{d}}x = a\ln 5} \) (i.e. \(2 \times \) their answer to (c)(i)) A1 N3
METHOD 2
changing variable
let \(w = x – 1\) , so \(\frac{{{\rm{d}}w}}{{{\rm{d}}x}} = 1\)
\(2\int {f(w){\rm{d}}w = } \frac{{2a}}{2}\ln ({w^2} + 1) + c\) (M1)
substituting correct limits
e.g. \(\left[ {a\ln \left[ {{{(x – 1)}^2} + 1} \right]} \right]_4^8\) , \(\left[ {a\ln ({w^2} + 1)} \right]_3^7\) , \(a\ln 50 – a\ln 10\) (M1)
\(\int_4^8 {2f(x – 1){\rm{d}}x = a\ln 5} \) A1 N3
[7 marks]
Question
The diagram below shows the graph of a function \(f(x)\) , for \( – 2 \le x \le 4\) .
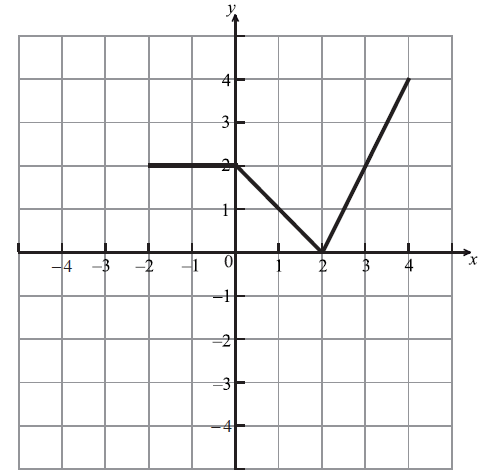
Let \(h(x) = f( – x)\) . Sketch the graph of \(h\) on the grid below.
Let \(g(x) = \frac{1}{2}f(x – 1)\) . The point \({\text{A}}(3{\text{, }}2)\) on the graph of \(f\) is transformed to the point P on the graph of \(g\) . Find the coordinates of P.
Answer/Explanation
Markscheme
A2 N2
[2 marks]
evidence of appropriate approach (M1)
e.g. reference to any horizontal shift and/or stretch factor, \(x = 3 + 1\) , \(y = \frac{1}{2} \times 2\)
P is \((4{\text{, }}1)\) (accept \(x = 4\) , \(y = 1\)) A1A1 N3
[3 marks]
Question
The following diagram shows the graph of a function \(f\), for −4 ≤ x ≤ 2.
On the same axes, sketch the graph of \(f\left( { – x} \right)\).
Another function, \(g\), can be written in the form \(g\left( x \right) = a \times f\left( {x + b} \right)\). The following diagram shows the graph of \(g\).
Write down the value of a and of b.
Answer/Explanation
Markscheme
A2 N2
[2 marks]
recognizing horizontal shift/translation of 1 unit (M1)
eg b = 1, moved 1 right
recognizing vertical stretch/dilation with scale factor 2 (M1)
eg a = 2, y ×(−2)
a = −2, b = −1 A1A1 N2N2
[4 marks]
Question
Let \(f(x) = 3{(x + 1)^2} – 12\) .
Show that \(f(x) = 3{x^2} + 6x – 9\) .
For the graph of f
(i) write down the coordinates of the vertex;
(ii) write down the y-intercept;
(iii) find both x-intercepts.
Hence sketch the graph of f .
Let \(g(x) = {x^2}\) . The graph of f may be obtained from the graph of g by the following two transformations
a stretch of scale factor t in the y-direction,
followed by a translation of \(\left( \begin{array}{l}
p\\
q
\end{array} \right)\) .
Write down \(\left( \begin{array}{l}
p\\
q
\end{array} \right)\) and the value of t .
Answer/Explanation
Markscheme
\(f(x) = 3({x^2} + 2x + 1) – 12\) A1
\( = 3{x^2} + 6x + 3 – 12\) A1
\( = 3{x^2} + 6x – 9\) AG N0
[2 marks]
(i) vertex is \(( – 1, – 12)\) A1A1 N2
(ii) \(y = – 9\) , or \((0, – 9)\) A1 N1
(iii) evidence of solving \(f(x) = 0\) M1
e.g. factorizing, formula
correct working A1
e.g. \(3(x + 3)(x – 1) = 0\) , \(x = \frac{{ – 6 \pm \sqrt {36 + 108} }}{6}\)
\(x = – 3\) , \(x = 1\) , or \(( – 3{\text{, }}0){\text{, }}(1{\text{, }}0)\) A1A1 N2
[7 marks]
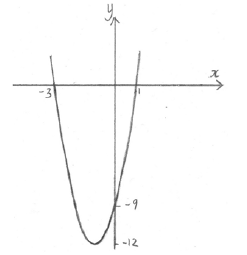A1A1A1 N3
Note: Award A1 for a parabola opening upward, A1 for vertex in approximately correct position, A1 for intercepts in approximately correct positions. Scale and labelling not required.
[3 marks]
\(\left( \begin{array}{l}
p\\
q
\end{array} \right) = \left( \begin{array}{l}
– 1\\
– 12
\end{array} \right)\) , \(t = 3\) A1A1A1 N3
[3 marks]