Question
Let \(f(x) = {\log _p}(x + 3)\) for \(x > – 3\) . Part of the graph of f is shown below.
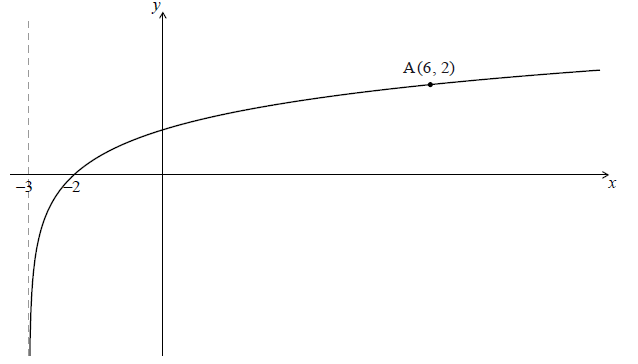
The graph passes through A(6, 2) , has an x-intercept at (−2, 0) and has an asymptote at \(x = – 3\) .
Find p .
The graph of f is reflected in the line \(y = x\) to give the graph of g .
(i) Write down the y-intercept of the graph of g .
(ii) Sketch the graph of g , noting clearly any asymptotes and the image of A.
The graph of \(f\) is reflected in the line \(y = x\) to give the graph of \(g\) .
Find \(g(x)\) .
Answer/Explanation
Markscheme
evidence of substituting the point A (M1)
e.g. \(2 = {\log _p}(6 + 3)\)
manipulating logs A1
e.g. \({p^2} = 9\)
\(p = 3\) A2 N2
[4 marks]
(i) \(y = – 2\) (accept \((0{\text{, }} – 2))\) A1 N1
(ii)
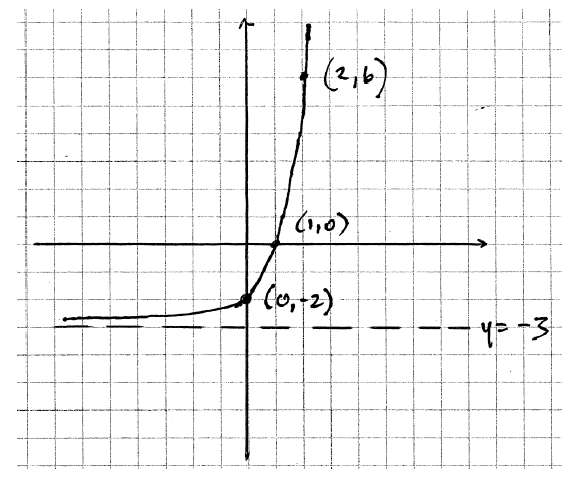 A1A1A1A1 N4
A1A1A1A1 N4
Note: Award A1 for asymptote at \(y = – 3\) , A1 for an increasing function that is concave up, A1 for a positive x-intercept and a negative y-intercept, A1 for passing through the point \((2{\text{, }}6)\) .
[5 marks]
METHOD 1
recognizing that \(g = {f^{ – 1}}\) (R1)
evidence of valid approach (M1)
e.g. switching x and y (seen anywhere), solving for x
correct manipulation (A1)
e.g. \({3^x} = y + 3\)
\(g(x) = {3^x} – 3\) A1 N3
METHOD 2
recognizing that \(g(x) = {a^x} + b\) (R1)
identifying vertical translation (A1)
e.g. graph shifted down 3 units, \(f(x) – 3\)
evidence of valid approach (M1)
e.g. substituting point to identify the base
\(g(x) = {3^x} – 3\) A1 N3
[4 marks]
Question
Find the value of \({\log _2}40 – {\log _2}5\) .
Find the value of \({8^{{{\log }_2}5}}\) .
Answer/Explanation
Markscheme
evidence of correct formula (M1)
eg \(\log a – \log b = \log \frac{a}{b}\) , \(\log \left( {\frac{{40}}{5}} \right)\) , \(\log 8 + \log 5 – \log 5\)
Note: Ignore missing or incorrect base.
correct working (A1)
eg \({\log _2}8\) , \({2^3} = 8\)
\({\log _2}40 – {\log _2}5 = 3\) A1 N2
[3 marks]
attempt to write \(8\) as a power of \(2\) (seen anywhere) (M1)
eg \({({2^3})^{{{\log }_2}5}}\) , \({2^3} = 8\) , \({2^a}\)
multiplying powers (M1)
eg \({2^{3{{\log }_2}5}}\) , \(a{\log _2}5\)
correct working (A1)
eg \({2^{{{\log }_2}125}}\) , \({\log _2}{5^3}\) , \({\left( {{2^{{{\log }_2}5}}} \right)^3}\)
\({8^{{{\log }_2}5}} = 125\) A1 N3
[4 marks]

