Question
Let \(f(x) = 3{\tan ^4}x + 2k\) and \(g(x) = – {\tan ^4}x + 8k{\tan ^2}x + k\), for \(0 \leqslant x \leqslant 1\), where \(0 < k < 1\). The graphs of \(f\) and \(g\) intersect at exactly one point. Find the value of \(k\).
Answer/Explanation
Markscheme
discriminant \( = 0\) (seen anywhere) M1
valid approach (M1)
eg\(\,\,\,\,\,\)\(f = g,{\text{ }}3{\tan ^4}x + 2k = – {\tan ^4}x + 8k{\tan ^2}x + k\)
rearranging their equation (to equal zero) (M1)
eg\(\,\,\,\,\,\)\(4{\tan ^4}x – 8k{\tan ^2}x + k = 0,{\text{ }}4{\tan ^4}x – 8k{\tan ^2}x + k\)
recognizing LHS is quadratic (M1)
eg\(\,\,\,\,\,\)\(4{({\tan ^2}x)^2} – 8k{\tan ^2}x + k = 0,{\text{ }}4{m^2} – 8km + k\)
correct substitution into discriminant A1
eg\(\,\,\,\,\,\)\({( – 8k)^2} – 4(4)(k)\)
correct working to find discriminant or solve discriminant \( = 0\) (A1)
eg\(\,\,\,\,\,\)\(64{k^2} – 16k,{\text{ }}\frac{{ – ( – 16) \pm \sqrt {{{16}^2}} }}{{2 \times 64}}\)
correct simplification (A1)
egx\(\,\,\,\,\,\)\(16k(4k – 1),{\text{ }}\frac{{32}}{{2 \times 64}}\)
\(k = \frac{1}{4}\) A1 N2
[8 marks]
Examiners report
There was a minor issue with the domain of the function, but this did not affect any candidate. The question was amended for publication.
Most candidates recognized the need to set the functions equal to each other and many rearranged the equation to equal zero. Few students then recognized the quadratic form and the need to find the discriminant. Those who did use the discriminant generally completed it correctly.
Question
Three consecutive terms of a geometric sequence are \(x – 3\), 6 and \(x + 2\).
Find the possible values of \(x\).
Answer/Explanation
Markscheme
METHOD 1
valid approach (M1)
eg\(\,\,\,\,\,\)\(r = \frac{6}{{x – 3}},{\text{ }}(x – 3) \times r = 6,{\text{ }}(x – 3){r^2} = x + 2\)
correct equation in terms of \(x\) only A1
eg\(\,\,\,\,\,\)\(\frac{6}{{x – 3}} = \frac{{x + 2}}{6},{\text{ }}(x – 3)(x + 2) = {6^2},{\text{ }}36 = {x^2} – x – 6\)
correct working (A1)
eg\(\,\,\,\,\,\)\({x^2} – x – 42,{\text{ }}{x^2} – x = 42\)
valid attempt to solve their quadratic equation (M1)
eg\(\,\,\,\,\,\)factorizing, formula, completing the square
evidence of correct working (A1)
eg\(\,\,\,\,\,\)\((x – 7)(x + 6),{\text{ }}\frac{{1 \pm \sqrt {169} }}{2}\)
\(x = 7,{\text{ }}x = – 6\) A1 N4
METHOD 2 (finding r first)
valid approach (M1)
eg\(\,\,\,\,\,\)\(r = \frac{6}{{x – 3}},{\text{ }}6r = x + 2,{\text{ }}(x – 3){r^2} = x + 2\)
correct equation in terms of \(r\) only A1
eg\(\,\,\,\,\,\)\(\frac{6}{r} + 3 = 6r – 2,{\text{ }}6 + 3r = 6{r^2} – 2r,{\text{ }}6{r^2} – 5r – 6 = 0\)
evidence of correct working (A1)
eg\(\,\,\,\,\,\)\((3r + 2)(2r – 3),{\text{ }}\frac{{5 \pm \sqrt {25 + 144} }}{{12}}\)
\(r = – \frac{2}{3},{\text{ }}r = \frac{3}{2}\) A1
substituting their values of \(r\) to find \(x\) (M1)
eg\(\,\,\,\,\,\)\((x – 3)\left( {\frac{2}{3}} \right) = 6,{\text{ }}x = 6\left( {\frac{3}{2}} \right) – 2\)
\(x = 7,{\text{ }}x = – 6\) A1 N4
[6 marks]
Examiners report
Nearly all candidates attempted to set up an expression, or pair of expressions, for the common ratio of the geometric sequence. When done correctly, these expressions led to a quadratic equation which was solved correctly by many candidates.
Question
A quadratic function \(f\) can be written in the form \(f(x) = a(x – p)(x – 3)\). The graph of \(f\) has axis of symmetry \(x = 2.5\) and \(y\)-intercept at \((0,{\text{ }} – 6)\)
Find the value of \(p\).
Find the value of \(a\).
The line \(y = kx – 5\) is a tangent to the curve of \(f\). Find the values of \(k\).
Answer/Explanation
Markscheme
METHOD 1 (using x-intercept)
determining that 3 is an \(x\)-intercept (M1)
eg\(\,\,\,\,\,\)\(x – 3 = 0\), 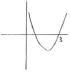
valid approach (M1)
eg\(\,\,\,\,\,\)\(3 – 2.5,{\text{ }}\frac{{p + 3}}{2} = 2.5\)
\(p = 2\) A1 N2
METHOD 2 (expanding f (x))
correct expansion (accept absence of \(a\)) (A1)
eg\(\,\,\,\,\,\)\(a{x^2} – a(3 + p)x + 3ap,{\text{ }}{x^2} – (3 + p)x + 3p\)
valid approach involving equation of axis of symmetry (M1)
eg\(\,\,\,\,\,\)\(\frac{{ – b}}{{2a}} = 2.5,{\text{ }}\frac{{a(3 + p)}}{{2a}} = \frac{5}{2},{\text{ }}\frac{{3 + p}}{2} = \frac{5}{2}\)
\(p = 2\) A1 N2
METHOD 3 (using derivative)
correct derivative (accept absence of \(a\)) (A1)
eg\(\,\,\,\,\,\)\(a(2x – 3 – p),{\text{ }}2x – 3 – p\)
valid approach (M1)
eg\(\,\,\,\,\,\)\(f’(2.5) = 0\)
\(p = 2\) A1 N2
[3 marks]
attempt to substitute \((0,{\text{ }} – 6)\) (M1)
eg\(\,\,\,\,\,\)\( – 6 = a(0 – 2)(0 – 3),{\text{ }}0 = a( – 8)( – 9),{\text{ }}a{(0)^2} – 5a(0) + 6a = – 6\)
correct working (A1)
eg\(\,\,\,\,\,\)\( – 6 = 6a\)
\(a = – 1\) A1 N2
[3 marks]
METHOD 1 (using discriminant)
recognizing tangent intersects curve once (M1)
recognizing one solution when discriminant = 0 M1
attempt to set up equation (M1)
eg\(\,\,\,\,\,\)\(g = f,{\text{ }}kx – 5 = – {x^2} + 5x – 6\)
rearranging their equation to equal zero (M1)
eg\(\,\,\,\,\,\)\({x^2} – 5x + kx + 1 = 0\)
correct discriminant (if seen explicitly, not just in quadratic formula) A1
eg\(\,\,\,\,\,\)\({(k – 5)^2} – 4,{\text{ }}25 – 10k + {k^2} – 4\)
correct working (A1)
eg\(\,\,\,\,\,\)\(k – 5 = \pm 2,{\text{ }}(k – 3)(k – 7) = 0,{\text{ }}\frac{{10 \pm \sqrt {100 – 4 \times 21} }}{2}\)
\(k = 3,{\text{ }}7\) A1A1 N0
METHOD 2 (using derivatives)
attempt to set up equation (M1)
eg\(\,\,\,\,\,\)\(g = f,{\text{ }}kx – 5 = – {x^2} + 5x – 6\)
recognizing derivative/slope are equal (M1)
eg\(\,\,\,\,\,\)\(f’ = {m_T},{\text{ }}f’ = k\)
correct derivative of \(f\) (A1)
eg\(\,\,\,\,\,\)\( – 2x + 5\)
attempt to set up equation in terms of either \(x\) or \(k\) M1
eg\(\,\,\,\,\,\)\(( – 2x + 5)x – 5 = – {x^2} + 5x – 6,{\text{ }}k\left( {\frac{{5 – k}}{2}} \right) – 5 = – {\left( {\frac{{5 – k}}{2}} \right)^2} + 5\left( {\frac{{5 – k}}{2}} \right) – 6\)
rearranging their equation to equal zero (M1)
eg\(\,\,\,\,\,\)\({x^2} – 1 = 0,{\text{ }}{k^2} – 10k + 21 = 0\)
correct working (A1)
eg\(\,\,\,\,\,\)\(x = \pm 1,{\text{ }}(k – 3)(k – 7) = 0,{\text{ }}\frac{{10 \pm \sqrt {100 – 4 \times 21} }}{2}\)
\(k = 3,{\text{ }}7\) A1A1 N0
[8 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
The following table shows the probability distribution of a discrete random variable \(A\), in terms of an angle \(\theta \).

Show that \(\cos \theta = \frac{3}{4}\).
Given that \(\tan \theta > 0\), find \(\tan \theta \).
Let \(y = \frac{1}{{\cos x}}\), for \(0 < x < \frac{\pi }{2}\). The graph of \(y\)between \(x = \theta \) and \(x = \frac{\pi }{4}\) is rotated 360° about the \(x\)-axis. Find the volume of the solid formed.
Answer/Explanation
Markscheme
evidence of summing to 1 (M1)
eg\(\,\,\,\,\,\)\(\sum {p = 1} \)
correct equation A1
eg\(\,\,\,\,\,\)\(\cos \theta + 2\cos 2\theta = 1\)
correct equation in \(\cos \theta \) A1
eg\(\,\,\,\,\,\)\(\cos \theta + 2(2{\cos ^2}\theta – 1) = 1,{\text{ }}4{\cos ^2}\theta + \cos \theta – 3 = 0\)
evidence of valid approach to solve quadratic (M1)
eg\(\,\,\,\,\,\)factorizing equation set equal to \(0,{\text{ }}\frac{{ – 1 \pm \sqrt {1 – 4 \times 4 \times ( – 3)} }}{8}\)
correct working, clearly leading to required answer A1
eg\(\,\,\,\,\,\)\((4\cos \theta – 3)(\cos \theta + 1),{\text{ }}\frac{{ – 1 \pm 7}}{8}\)
correct reason for rejecting \(\cos \theta \ne – 1\) R1
eg\(\,\,\,\,\,\)\(\cos \theta \) is a probability (value must lie between 0 and 1), \(\cos \theta > 0\)
Note: Award R0 for \(\cos \theta \ne – 1\) without a reason.
\(\cos \theta = \frac{3}{4}\) AG N0
valid approach (M1)
eg\(\,\,\,\,\,\)sketch of right triangle with sides 3 and 4, \({\sin ^2}x + {\cos ^2}x = 1\)
correct working
(A1)
eg\(\,\,\,\,\,\)missing side \( = \sqrt 7 ,{\text{ }}\frac{{\frac{{\sqrt 7 }}{4}}}{{\frac{3}{4}}}\)
\(\tan \theta = \frac{{\sqrt 7 }}{3}\) A1 N2
[3 marks]
attempt to substitute either limits or the function into formula involving \({f^2}\) (M1)
eg\(\,\,\,\,\,\)\(\pi \int_\theta ^{\frac{\pi }{4}} {{f^2},{\text{ }}\int {{{\left( {\frac{1}{{\cos x}}} \right)}^2}} } \)
correct substitution of both limits and function (A1)
eg\(\,\,\,\,\,\)\(\pi \int_\theta ^{\frac{\pi }{4}} {{{\left( {\frac{1}{{\cos x}}} \right)}^2}{\text{d}}x} \)
correct integration (A1)
eg\(\,\,\,\,\,\)\(\tan x\)
substituting their limits into their integrated function and subtracting (M1)
eg\(\,\,\,\,\,\)\(\tan \frac{\pi }{4} – \tan \theta \)
Note: Award M0 if they substitute into original or differentiated function.
\(\tan \frac{\pi }{4} = 1\) (A1)
eg\(\,\,\,\,\,\)\(1 – \tan \theta \)
\(V = \pi – \frac{{\pi \sqrt 7 }}{3}\) A1 N3
[6 marks]
Examiners report
[N/A]
[N/A]
[N/A]

