Download IITian Academy App for accessing Online Mock Tests and More..
Question
A city is concerned about pollution, and decides to look at the number of people using taxis. At the end of the year 2000, there were 280 taxis in the city. After n years the number of taxis, T, in the city is given by\[T = 280 \times {1.12^n} .\]
(i) Find the number of taxis in the city at the end of 2005.
(ii) Find the year in which the number of taxis is double the number of taxis there were at the end of 2000.
At the end of 2000 there were \(25600\) people in the city who used taxis.
After n years the number of people, P, in the city who used taxis is given by\[P = \frac{{2560000}}{{10 + 90{{\rm{e}}^{ – 0.1n}}}} .\](i) Find the value of P at the end of 2005, giving your answer to the nearest whole number.
(ii) After seven complete years, will the value of P be double its value at the end of 2000? Justify your answer.
Let R be the ratio of the number of people using taxis in the city to the number of taxis. The city will reduce the number of taxis if \(R < 70\) .
(i) Find the value of R at the end of 2000.
(ii) After how many complete years will the city first reduce the number of taxis?
Answer/Explanation
Markscheme
(i) \(n = 5\) (A1)
\(T = 280 \times {1.12^5}\)
\(T = 493\) A1 N2
(ii) evidence of doubling (A1)
e.g. 560
setting up equation A1
e.g. \(280 \times {1.12^n} = 560\), \({1.12^n} = 2\)
\(n = 6.116 \ldots \) (A1)
in the year 2007 A1 N3
[6 marks]
(i) \(P = \frac{{2560000}}{{10 + 90{{\rm{e}}^{ – 0.1(5)}}}}\) (A1)
\(P = 39635.993 \ldots \) (A1)
\(P = 39636\) A1 N3
(ii) \(P = \frac{{2560000}}{{10 + 90{{\rm{e}}^{ – 0.1(7)}}}}\)
\(P = 46806.997 \ldots \) A1
not doubled A1 N0
valid reason for their answer R1
e.g. \(P < 51200\)
[6 marks]
(i) correct value A2 N2
e.g. \(\frac{{25600}}{{280}}\) , 91.4, \(640:7\)
(ii) setting up an inequality (accept an equation, or reversed inequality) M1
e.g. \(\frac{P}{T} < 70\) , \(\frac{{2560000}}{{(10 + 90{{\rm{e}}^{ – 0.1n}})280 \times {{1.12}^n}}} < 70\)
finding the value \(9.31 \ldots \) (A1)
after 10 years A1 N2
[5 marks]
Question
A farmer wishes to create a rectangular enclosure, ABCD, of area 525 m2, as shown below.
The fencing used for side AB costs \(\$ 11\) per metre. The fencing for the other three sides costs \(\$ 3\) per metre. The farmer creates an enclosure so that the cost is a minimum. Find this minimum cost.
Answer/Explanation
Markscheme
METHOD 1
correct expression for second side, using area = 525 (A1)
e.g. let \({\rm{AB}} = x\) , \({\rm{AD}} = \frac{{525}}{x}\)
attempt to set up cost function using $3 for three sides and $11 for one side (M1)
e.g. \(3({\rm{AD}} + {\rm{BC}} + {\rm{CD}}) + 11{\rm{AB}}\)
correct expression for cost A2
e.g. \(\frac{{525}}{x} \times 3 + \frac{{525}}{x} \times 3 + 11x + 3x\) , \(\frac{{525}}{{{\rm{AB}}}} \times 3 + \frac{{525}}{{{\rm{AB}}}} \times 3 + 11{\rm{AB}} + 3{\rm{AB}}\) , \(\frac{{3150}}{x} + 14x\)
EITHER
sketch of cost function (M1)
identifying minimum point (A1)
e.g. marking point on graph, \(x = 15\)
minimum cost is 420 (dollars) A1 N4
OR
correct derivative (may be seen in equation below) (A1)
e.g. \(C'(x) = \frac{{ – 1575}}{{{x^2}}} + \frac{{ – 1575}}{{{x^2}}} + 14\)
setting their derivative equal to 0 (seen anywhere) (M1)
e.g. \(\frac{{ – 3150}}{{{x^2}}} + 14 = 0\)
minimum cost is 420 (dollars) A1 N4
METHOD 2
correct expression for second side, using area = 525 (A1)
e.g. let \({\rm{AD}} = x\) , \({\rm{AB}} = \frac{{525}}{x}\)
attempt to set up cost function using \(\$ 3\) for three sides and \(\$ 11\) for one side (M1)
e.g. \(3({\rm{AD}} + {\rm{BC}} + {\rm{CD}}) + 11{\rm{AB}}\)
correct expression for cost A2
e.g. \(3\left( {x + x + \frac{{525}}{x}} \right) + \frac{{525}}{x} \times 11\) , \(3\left( {{\rm{AD}} + {\rm{AD}} + \frac{{525}}{{{\rm{AD}}}}} \right) + \frac{{525}}{{{\rm{AD}}}} \times 11\) , \(6x + \frac{{7350}}{x}\)
EITHER
sketch of cost function (M1)
identifying minimum point (A1)
e.g. marking point on graph, \(x = 35\)
minimum cost is 420 (dollars) A1 N4
OR
correct derivative (may be seen in equation below) (A1)
e.g. \(C'(x) = 6 – \frac{{7350}}{{{x^2}}}\)
setting their derivative equal to 0 (seen anywhere) (M1)
e.g. \(6 – \frac{{7350}}{{{x^2}}} = 0\)
minimum cost is 420 (dollars) A1 N4
[7 marks]
Question
The number of bacteria, n , in a dish, after t minutes is given by \(n = 800{{\rm{e}}^{0.13t}}\) .
Find the value of n when \(t = 0\) .
Find the rate at which n is increasing when \(t = 15\) .
Answer/Explanation
Markscheme
\(n = 800{{\rm{e}}^0}\) (A1)
\(n = 800\) A1 N2
[2 marks]
evidence of using the derivative (M1)
\(n'(15) = 731\) A1 N2
[2 marks]
METHOD 1
setting up inequality (accept equation or reverse inequality) A1
e.g. \(n'(t) > 10000\)
evidence of appropriate approach M1
e.g. sketch, finding derivative
\(k = 35.1226 \ldots \) (A1)
least value of k is 36 A1 N2
METHOD 2
\(n'(35) = 9842\) , and \(n'(36) = 11208\) A2
least value of k is 36 A2 N2
[4 marks]
Question
Jose takes medication. After t minutes, the concentration of medication left in his bloodstream is given by \(A(t) = 10{(0.5)^{0.014t}}\) , where A is in milligrams per litre.
Write down \(A(0)\) .
Find the concentration of medication left in his bloodstream after 50 minutes.
At 13:00, when there is no medication in Jose’s bloodstream, he takes his first dose of medication. He can take his medication again when the concentration of medication reaches 0.395 milligrams per litre. What time will Jose be able to take his medication again?
Answer/Explanation
Markscheme
\(A(0) = 10\) A1 N1
[1 mark]
substitution into formula (A1)
e.g. \(10{(0.5)^{0.014(50)}}\) , \(A(50)\)
\(A(50) = 6.16\) A1 N2
[2 marks]
set up equation (M1)
e.g. \(A(t) = 0.395\)
attempting to solve (M1)
e.g. graph, use of logs
correct working (A1)
e.g. sketch of intersection, \(0.014t\log 0.5 = \log 0.0395\)
\(t = 333.00025 \ldots \) A1
correct time 18:33 or 18:34 (accept 6:33 or 6:34 but nothing else) A1 N3
[5 marks]
Question
The following diagram shows two ships A and B. At noon, ship A was 15 km due north of ship B. Ship A was moving south at 15 km h–1 and ship B was moving east at 11 km h–1.
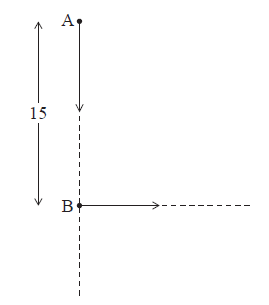
Find the distance between the ships
(i) at 13:00;
(ii) at 14:00.
Let \(s(t)\) be the distance between the ships t hours after noon, for \(0 \le t \le 4\) .
Show that \(s(t) = \sqrt {346{t^2} – 450t + 225} \) .
Sketch the graph of \(s(t)\) .
Due to poor weather, the captain of ship A can only see another ship if they are less than 8 km apart. Explain why the captain cannot see ship B between noon and 16:00.
Answer/Explanation
Markscheme
(i) evidence of valid approach (M1)
e.g. ship A where B was, B \(11{\text{ km}}\) away
\({\text{distance}} = 11\) A1 N2
(ii) evidence of valid approach (M1)
e.g. new diagram, Pythagoras, vectors
\(s = \sqrt {{{15}^2} + {{22}^2}} \) (A1)
\(\sqrt {709} = 26.62705\)
\(s = 26.6\) A1 N2
Note: Award M0A0A0 for using the formula given in part (b).
[5 marks]
evidence of valid approach (M1)
e.g. a table, diagram, formula \(d = r \times t\)
distance ship A travels t hours after noon is \(15(t – 1)\) (A2)
distance ship B travels in t hours after noon is \(11t\) (A1)
evidence of valid approach M1
e.g. \(s(t) = \sqrt {{{\left[ {15(t – 1)} \right]}^2} + {{(11t)}^2}} \)
correct simplification A1
e.g. \(\sqrt {225({t^2} – 2t + 1) + 121{t^2}} \)
\(s(t) = \sqrt {346{t^2} – 450t + 225} \) AG N0
[6 marks]
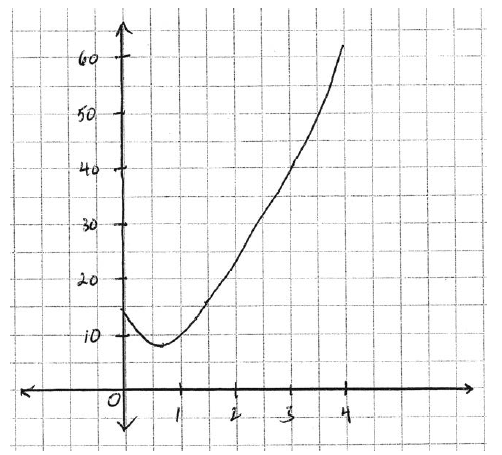A1A1A1 N3
Note: Award A1 for shape, A1 for minimum at approximately \((0.7{\text{, }}9)\), A1 for domain.
[3 marks]
evidence of valid approach (M1)
e.g. \(s'(t) = 0\) , find minimum of \(s(t)\) , graph, reference to “more than 8 km”
\(\min = 8.870455 \ldots \) (accept 2 or more sf) A1
since \({s_{\min}} > 8\) , captain cannot see ship B R1 N0
[3 marks]
Question
The number of bacteria in two colonies, \(\rm{A}\) and \(\rm{B}\), starts increasing at the same time.
The number of bacteria in colony \(\rm{A}\) after \(t\) hours is modelled by the function \(\rm{A}(t) = 12{{\text{e}}^{0.4t}}\).
Find the number of bacteria in colony \({\text{A}}\) after four hours.
Find the number of bacteria in colony \({\text{A}}\) after four hours.
How long does it take for the number of bacteria in colony \({\text{A}}\) to reach \(400\)?
The number of bacteria in colony \({\text{B}}\) after \(t\) hours is modelled by the function \(B(t) = 24{{\text{e}}^{kt}}\).
After four hours, there are \(60\) bacteria in colony \({\text{B}}\). Find the value of \(k\).
The number of bacteria in colony \({\text{B}}\) after \(t\) hours is modelled by the function \(B(t) = 24{{\text{e}}^{kt}}\).
The number of bacteria in colony \({\text{A}}\) first exceeds the number of bacteria in colony \({\text{B}}\) after \(n\) hours, where \(n \in \mathbb{Z}\). Find the value of \(n\).
Answer/Explanation
Markscheme
correct substitution into formula (A1)
eg \(12{{\text{e}}^{0.4(0)}}\)
\(12\) bacteria in the dish A1 N2
[2 marks]
correct substitution into formula (A1)
eg \(12{{\text{e}}^{0.4(4)}}\)
\(59.4363\) (A1)
\(59\) bacteria in the dish (integer answer only) A1 N3
[3 marks]
correct equation (A1)
eg \(A(t) = 400,{\text{ }}12{{\text{e}}^{0.4t}} = 400\)
valid attempt to solve (M1)
eg graph, use of logs
\(8.76639\)
\(8.77\) (hours) A1 N3
[3 marks]
valid attempt to solve (M1)
eg \(n(4) = 60,{\text{ }}60 = 24{{\text{e}}^{4k}}\), use of logs
correct working (A1)
eg sketch of intersection, \(4k = \ln 2.5\)
\(k = 0.229072\)
\(k = \frac{{\ln 2.5}}{4}\) (exact), \(k = 0.229\) A1 N3
[3 marks]
METHOD 1
setting up an equation or inequality (accept any variable for \(n\)) (M1)
eg \(A(t) > B(t),{\text{ }}12{{\text{e}}^{0.4n}} = 24{{\text{e}}^{0.229n}},{\text{ }}{{\text{e}}^{0.4n}} = 2{{\text{e}}^{0.229n}}\)
correct working (A1)
eg sketch of intersection, \({{\text{e}}^{0.171n}} = 2\)
\(4.05521\) (accept \(4.05349\)) (A1)
\(n = 5\) (integer answer only) A1 N3
METHOD 2
\(A(4) = 59,{\text{ }}B(4) = 60\) (from earlier work)
\(A(5) = 88.668,{\text{ }}B(5) = 75.446\) A1A1
valid reasoning (R1)
eg \(A(4) < B(4)\) and \(A(5) > B(5)\)
\(n = 5\) (integer answer only) A1 N3
[4 marks]
Question
Let \(G(x) = 95{{\text{e}}^{( – 0.02x)}} + 40\), for \(20 \le x \le 200\).
On the following grid, sketch the graph of \(G\).
Robin and Pat are planning a wedding banquet. The cost per guest, \(G\) dollars, is modelled by the function \(G(n) = 95{{\text{e}}^{( – 0.02n)}} + 40\), for \(20 \le n \le 200\), where \(n\) is the number of guests.
Calculate the total cost for \(45\) guests.
Answer/Explanation
Markscheme
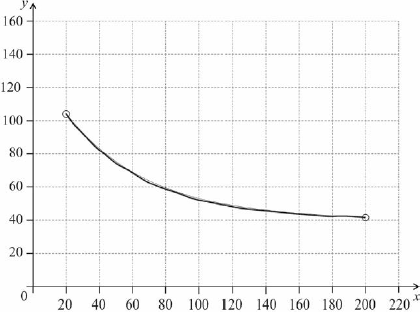A1A1A1 N3
Note: Curve must be approximately correct exponential shape (concave up and decreasing). Only if the shape is approximately correct, award the following:
A1 for left endpoint in circle,
A1 for right endpoint in circle,
A1 for asymptotic to \(y = 40\) (must not go below \(y = 40\)).
[3 marks]
attempt to find \(G(45)\) (M1)
eg\(\;\;\;78.6241\), value read from their graph
multiplying cost times number of people (M1)
eg\(\;\;\;45 \times 78.6241,{\text{ }}G(45) \times 45\)
\(3538.08\)
\(3540\) (dollars) A1 N2
[3 marks]
Total [6 marks]
Question
The following diagram shows a square \(ABCD\), and a sector \(OAB\) of a circle centre \(O\), radius \(r\). Part of the square is shaded and labelled \(R\).
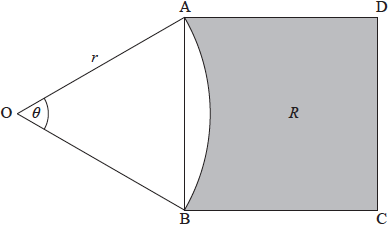
\[{\rm{A\hat OB}} = \theta {\text{, where }}0.5 \ \le \ \theta < \pi .\]
Show that the area of the square \(ABCD\) is \(2{r^2}(1 – \cos \theta )\).
When \(\theta = \alpha \), the area of the square \(ABCD\) is equal to the area of the sector \(OAB\).
(i) Write down the area of the sector when \(\theta = \alpha \).
(ii) Hence find \(\alpha \).
When \(\theta = \beta \), the area of \(R\) is more than twice the area of the sector.
Find all possible values of \(\beta \).
Answer/Explanation
Markscheme
area of \({\text{ABCD}} = {\text{A}}{{\text{B}}^2}\) (seen anywhere) (A1)
choose cosine rule to find a side of the square (M1)
eg\(\;\;\;{a^2} = {b^2} + {c^2} – 2bc\cos \theta \)
correct substitution (for triangle \(AOB\)) A1
eg\(\;\;\;{r^2} + {r^2} – 2 \times r \times r\cos \theta ,{\text{ O}}{{\text{A}}^2} + {\text{O}}{{\text{B}}^2} – 2 \times {\text{OA}} \times {\text{OB}}\cos \theta \)
correct working for \({\text{A}}{{\text{B}}^2}\) A1
eg\(\;\;\;2{r^{\text{2}}} – 2{r^2}\cos \theta \)
\({\text{area}} = 2{r^2}(1 – \cos \theta )\) AG N0
Note: Award no marks if the only working is \(2{r^2} – 2{r^2}\cos \theta \).
[4 marks]
(i) \(\frac{1}{2}\alpha {r^2}\;\;\;\left( {{\text{accept }}2{r^2}(1 – \cos \alpha )} \right)\) A1 N1
(ii) correct equation in one variable (A1)
eg\(\;\;\;2(1 – \cos \alpha ) = \frac{1}{2}\alpha \)
\(\alpha = 0.511024\)
\(\alpha = 0.511\;\;\;({\text{accept }}\theta = 0.511)\) A2 N2
Note: Award A1 for \(\alpha = 0.511\) and additional answers.
[4 marks]
Note: In this part, accept \(\theta \) instead of \(\beta \), and the use of equations instead of inequalities in the working.
attempt to find \(R\) (M1)
eg\(\;\;\;\)subtraction of areas, \({\text{square}} – {\text{segment}}\)
correct expression for segment area (A1)
eg\(\;\;\;\frac{1}{2}\beta {r^2} – \frac{1}{2}{r^2}\sin \beta \)
correct expression for \(R\) (A1)
eg\(\;\;\;2{r^2}(1 – \cos \beta ) – \left( {\frac{1}{2}\beta {r^2} – \frac{1}{2}{r^2}\sin \beta } \right)\)
correct inequality (A1)
eg\(\;\;\;2{r^2}(1 – \cos \beta ) – \left( {\frac{1}{2}\beta {r^2} – \frac{1}{2}{r^2}\sin \beta } \right) > 2\left( {\frac{1}{2}\beta {r^2}} \right)\)
correct inequality in terms of angle only A1
eg\(\;\;\;2(1 – \cos \beta ) – \left( {\frac{1}{2}\beta – \frac{1}{2}\sin \beta } \right) > \beta \)
attempt to solve their inequality, must represent \(R > \) twice sector (M1)
eg\(\;\;\;\)sketch, one correct value
Note: Do not award the second (M1) unless the first (M1) for attempting to find \(R\) has been awarded.
both correct values \(1.30573\) and \(2.67369\) (A1)
correct inequality \(1.31 < \beta < 2.67\) A1 N3
[8 marks]
Total [16 marks]
Question
An environmental group records the numbers of coyotes and foxes in a wildlife reserve after \(t\) years, starting on 1 January 1995.
Let \(c\) be the number of coyotes in the reserve after \(t\) years. The following table shows the number of coyotes after \(t\) years.
The relationship between the variables can be modelled by the regression equation \(c = at + b\).
Find the value of \(a\) and of \(b\).
Use the regression equation to estimate the number of coyotes in the reserve when \(t = 7\).
Let \(f\) be the number of foxes in the reserve after \(t\) years. The number of foxes can be modelled by the equation \(f = \frac{{2000}}{{1 + 99{{\text{e}}^{ – kt}}}}\), where \(k\) is a constant.
Find the number of foxes in the reserve on 1 January 1995.
After five years, there were 64 foxes in the reserve. Find \(k\).
During which year were the number of coyotes the same as the number of foxes?
Answer/Explanation
Markscheme
evidence of setup (M1)
eg\(\;\;\;\)correct value for \(a\) or \(b\)
\(13.3823\), \(137.482\)
\(a{\rm{ }} = {\rm{ }}13.4\), \(b{\rm{ }} = {\rm{ }}137\) A1A1 N3
[3 marks]
correct substitution into their regression equation
eg\(\;\;\;13.3823 \times 7 + 137.482\) (A1)
correct calculation
\(231.158\) (A1)
\(231\) (coyotes) (must be an integer) A1 N2
[3 marks]
recognizing \(t = 0\) (M1)
eg\(\;\;\;f(0)\)
correct substitution into the model
eg\(\;\;\;\frac{{2000}}{{1 + 99{{\text{e}}^{ – k(0)}}}},{\text{ }}\frac{{2000}}{{100}}\) (A1)
\(20\) (foxes) A1 N2
[3 marks]
recognizing \((5,{\text{ }}64)\) satisfies the equation (M1)
eg\(\;\;\;f(5) = 64\)
correct substitution into the model
eg\(\;\;\;64 = \frac{{2000}}{{1 + 99{{\text{e}}^{ – k(5)}}}},{\text{ }}64(1 + 99\(e\)^{ – 5k}}) = 2000\) (A1)
\(0.237124\)
\(k = – \frac{1}{5}\ln \left( {\frac{{11}}{{36}}} \right){\text{ (exact), }}0.237{\text{ }}[0.237,{\text{ }}0.238]\) A1 N2
[3 marks]
valid approach (M1)
eg\(\;\;\;c = f\), sketch of graphs
correct working (A1)
eg\(\;\;\;\frac{{2000}}{{1 + 99{{\text{e}}^{ – 0.237124t}}}} = 13.382t + 137.482\), sketch of graphs, table of values
\(t = 12.0403\) (A1)
\(2007\) A1 N2
Note: Exception to the FT rule. Award A1FT on their value of \(t\).
[4 marks]
Total [16 marks]
Question
A rock falls off the top of a cliff. Let \(h\) be its height above ground in metres, after \(t\) seconds.
The table below gives values of \(h\) and \(t\) .
Jane thinks that the function \(f(t) = – 0.25{t^3} – 2.32{t^2} + 1.93t + 106\) is a suitable model for the data. Use Jane’s model to
(i) write down the height of the cliff;
(ii) find the height of the rock after 4.5 seconds;
(iii) find after how many seconds the height of the rock is \(30{\text{ m}}\).
Kevin thinks that the function \(g(t) = – 5.2{t^2} + 9.5t + 100\) is a better model for the data. Use Kevin’s model to find when the rock hits the ground.
(i) On graph paper, using a scale of 1 cm to 1 second, and 1 cm to 10 m, plot the data given in the table.
(ii) By comparing the graphs of f and g with the plotted data, explain which function is a better model for the height of the falling rock.
Answer/Explanation
Markscheme
(i) \(106{\text{ m}}\) A1 N1
(ii) substitute \(t = 4.5\) M1
\(h = 44.9{\text{ m}}\) A1 N2
(iii) set up suitable equation M1
e.g. \(f(t) = 30\)
\(t = 4.91\) A1 N1
[5 marks]
recognizing that height is 0 A1
set up suitable equation M1
e.g. \(g(t) = 0\)
\(t = 5.39{\text{ secs}}\) A1 N2
[3 marks]
A1A2 N3
Note: Award A1 for correct scales on axes, A2 for 5 correct points, A1 for 3 or 4 correct points.
(ii) Jane’s function, with 2 valid reasons A1R1R1 N3
e.g. Jane’s passes very close to all the points, Kevin’s has the rock clearly going up initially – not possible if rock falls
Note: Although Jane’s also goes up initially, it only goes up very slightly, and so is the better model.
[6 marks]