Question
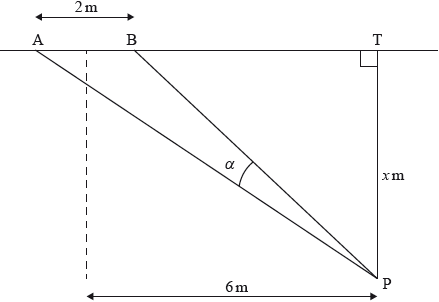
Points A , B and T lie on a line on an indoor soccer field. The goal, [AB] , is 2 metres wide. A player situated at point P kicks a ball at the goal. [PT] is perpendicular to (AB) and is 6 metres from a parallel line through the centre of [AB] . Let PT be \(x\) metros and let \(\alpha = {\rm{A\hat PB}}\) measured in degrees. Assume that the ball travels along the floor.
The maximum for \(\tan \alpha \) gives the maximum for \(\alpha \).
a.Find the value of \(\alpha \) when \(x = 10\).[4]
b.Show that \(\tan \alpha = \frac{{2x}}{{{x^2} + 35}}\).[4]
c.(i) Find \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha )\).
(ii) Hence or otherwise find the value of \(\alpha \) such that \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = 0\).
(iii) Find \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) and hence show that the value of \(\alpha \) never exceeds 10°.[11]
d.Find the set of values of \(x\) for which \(\alpha \geqslant 7^\circ \).[3]
▶️Answer/Explanation
Markscheme
EITHER
\(\alpha = \arctan \frac{7}{{10}} – \arctan \frac{5}{{10}}{\text{ }}( = 34.992 \ldots ^\circ – 26.5651 \ldots ^\circ )\) (M1)(A1)(A1)
Note: Award (M1) for \(\alpha = {\rm{A\hat PT}} – {\rm{B\hat PT}}\), (A1) for a correct \({\rm{A\hat PT}}\) and (A1) for a correct \({\rm{B\hat PT}}\).
OR
\(\alpha = \arctan {\text{ }}2 – \arctan \frac{{10}}{7}{\text{ }}( = 63.434 \ldots ^\circ – 55.008 \ldots ^\circ )\) (M1)(A1)(A1)
Note: Award (M1) for \(\alpha = {\rm{P\hat BT}} – {\rm{P\hat AT}}\), (A1) for a correct \({\rm{P\hat BT}}\) and (A1) for a correct \({\rm{P\hat AT}}\).
OR
\(\alpha = \arccos \left( {\frac{{125 + 149 – 4}}{{2 \times \sqrt {125} \times \sqrt {149} }}} \right)\) (M1)(A1)(A1)
Note: Award (M1) for use of cosine rule, (A1) for a correct numerator and (A1) for a correct denominator.
THEN
\( = 8.43^\circ \) A1
[4 marks]
EITHER
\(\tan \alpha = \frac{{\frac{7}{x} – \frac{5}{x}}}{{1 + \left( {\frac{7}{x}} \right)\left( {\frac{5}{x}} \right)}}\) M1A1A1
Note: Award M1 for use of \(\tan (A – B)\), A1 for a correct numerator and A1 for a correct denominator.
\( = \frac{{\frac{2}{x}}}{{1 + \frac{{35}}{{{x^2}}}}}\) M1
OR
\(\tan \alpha = \frac{{\frac{x}{5} – \frac{x}{7}}}{{1 + \left( {\frac{x}{5}} \right)\left( {\frac{x}{7}} \right)}}\) M1A1A1
Note: Award M1 for use of xxx, A1 for a correct numerator and A1 for a correct denominator.
\( = \frac{{\frac{{2x}}{{35}}}}{{1 + \frac{{{x^2}}}{{35}}}}\) M1
OR
\(\cos \alpha = \frac{{{x^2} + 35}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}\) M1A1
Note: Award M1 for either use of the cosine rule or use of \(\cos (A – B)\).
\(\sin \alpha \frac{{2x}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}\) A1
\(\tan \alpha = \frac{{\frac{{2x}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}}}{{\frac{{{x^2} + 35}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}}}\) M1
THEN
\(\tan \alpha = \frac{{2x}}{{{x^2} + 35}}\) AG
[4 marks]
(i) \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = \frac{{2({x^2} + 35) – (2x)(2x)}}{{{{({x^2} + 35)}^2}}}{\text{ }}\left( { = \frac{{70 – 2{x^2}}}{{{{({x^2} + 35)}^2}}}} \right)\) M1A1A1
Note: Award M1 for attempting product or quotient rule differentiation, A1 for a correct numerator and A1 for a correct denominator.
(ii) METHOD 1
EITHER
\(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = 0 \Rightarrow 70 – 2{x^2} = 0\) (M1)
\(x = \sqrt {35} {\text{ (m) }}\left( { = 5.9161 \ldots {\text{ (m)}}} \right)\) A1
\(\tan \alpha = \frac{1}{{\sqrt {35} }}{\text{ }}( = 0.16903 \ldots )\) (A1)
OR
attempting to locate the stationary point on the graph of
\(\tan \alpha = \frac{{2x}}{{{x^2} + 35}}\) (M1)
\(x = 5.9161 \ldots {\text{ (m) }}\left( { = \sqrt {35} {\text{ (m)}}} \right)\) A1
\(\tan \alpha = 0.16903 \ldots {\text{ }}\left( { = \frac{1}{{\sqrt {35} }}} \right)\) (A1)
THEN
\(\alpha = 9.59^\circ \) A1
METHOD 2
EITHER
\(\alpha = \arctan \left( {\frac{{2x}}{{{x^2} + 35}}} \right) \Rightarrow \frac{{{\text{d}}\alpha }}{{{\text{d}}x}} = \frac{{70 – 2{x^2}}}{{{{({x^2} + 35)}^2} + 4{x^2}}}\) M1
\(\frac{{{\text{d}}\alpha }}{{{\text{d}}x}} = 0 \Rightarrow x = \sqrt {35} {\text{ (m) }}\left( { = 5.9161{\text{ (m)}}} \right)\) A1
OR
attempting to locate the stationary point on the graph of
\(\alpha = \arctan \left( {\frac{{2x}}{{{x^2} + 35}}} \right)\) (M1)
\(x = 5.9161 \ldots {\text{ (m) }}\left( { = \sqrt {35} {\text{ (m)}}} \right)\) A1
THEN
\(\alpha = 0.1674 \ldots {\text{ }}\left( { = \arctan \frac{1}{{\sqrt {35} }}} \right)\) (A1)
\( = 9.59^\circ \) A1
(iii) \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha ) = \frac{{{{({x^2} + 25)}^2}( – 4x) – (2)(2x)({x^2} + 35)(70 – 2{x^2})}}{{{{({x^2} + 35)}^4}}}{\text{ }}\left( { = \frac{{4x({x^2} – 105)}}{{{{({x^2} + 35)}^3}}}} \right)\) M1A1
substituting \(x = \sqrt {35} {\text{ }}( = 5.9161 \ldots )\) into \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) M1
\(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha ) < 0{\text{ }}( =- 0.004829 \ldots )\) and so \(\alpha = 9.59^\circ \) is the maximum value of \(\alpha \) R1
\(\alpha \) never exceeds 10° AG
[11 marks]
attempting to solve \(\frac{{2x}}{{{x^2} + 35}} \geqslant \tan 7^\circ \) (M1)
Note: Award (M1) for attempting to solve \(\frac{{2x}}{{{x^2} + 35}} = \tan 7^\circ \).
\(x = 2.55\) and \(x = 13.7\) (A1)
\(2.55 \leqslant x \leqslant 13.7{\text{ (m)}}\) A1
[3 marks]
Question
a.Let \(z = r(\cos \alpha + {\text{i}}\sin \alpha )\), where \(\alpha \) is measured in degrees, be the solution of \({z^5} – 1 = 0\) which has the smallest positive argument.
(i) Use the binomial theorem to expand \({(\cos \theta + {\text{i}}\sin \theta )^5}\).
(ii) Hence use De Moivre’s theorem to prove
\[\sin 5\theta = 5{\cos ^4}\theta \sin \theta – 10{\cos ^2}\theta {\sin ^3}\theta + {\sin ^5}\theta .\]
(iii) State a similar expression for \(\cos 5\theta \) in terms of \(\cos \theta \) and \(\sin \theta \).[6]
▶️Answer/Explanation
Markscheme
(i) \({(\cos \theta + {\text{i}}\sin \theta )^5}\)
\( = {\cos ^5}\theta + 5{\text{i}}{\cos ^4}\theta \sin \theta + 10{{\text{i}}^2}{\cos ^3}\theta {\sin ^2}\theta + \)
\(10{{\text{i}}^3}{\cos ^2}\theta {\sin ^3}\theta + 5{{\text{i}}^4}\cos \theta {\sin ^4}\theta + {{\text{i}}^5}{\sin ^5}\theta \) A1A1
\(( = {\cos ^5}\theta + 5{\text{i}}{\cos ^4}\theta \sin \theta – 10{\cos ^3}\theta {\sin ^2}\theta – \)
\(10{\text{i}}{\cos ^2}\theta {\sin ^3}\theta + 5\cos \theta {\sin ^4}\theta + {\text{i}}{\sin ^5}\theta )\)
Note: Award first A1 for correct binomial coefficients.
(ii) \({({\text{cis}}\theta )^5} = {\text{cis}}5\theta = \cos 5\theta + {\text{i}}\sin 5\theta \) M1
\( = {\cos ^5}\theta + 5{\text{i}}{\cos ^4}\theta \sin \theta – 10{\cos ^3}\theta {\sin ^2}\theta – 10{\text{i}}{\cos ^2}\theta {\sin ^3}\theta + \)
\(5\cos \theta {\sin ^4}\theta + {\text{i}}{\sin ^5}\theta \) A1
Note: Previous line may be seen in (i)
equating imaginary terms M1
\(\sin 5\theta = 5{\cos ^4}\theta \sin \theta – 10{\cos ^2}\theta {\sin ^3}\theta + {\sin ^5}\theta \) AG
(iii) equating real terms
\(\cos 5\theta = {\cos ^5}\theta – 10{\cos ^3}\theta {\sin ^2}\theta + 5\cos \theta {\sin ^4}\theta \) A1
[6 marks]
\({(r{\text{cis}}\alpha )^5} = 1 \Rightarrow {r^5}{\text{cis}}5\alpha = 1{\text{cis}}0\) M1
\({r^5} = 1 \Rightarrow r = 1\) A1
\(5\alpha = 0 \pm 360k,{\text{ }}k \in \mathbb{Z} \Rightarrow a = 72k\) (M1)
\(\alpha = 72^\circ \) A1
Note: Award M1A0 if final answer is given in radians.
[4 marks]
use of \(\sin (5 \times 72) = 0\) OR the imaginary part of \(1\) is \(0\) (M1)
\(0 = 5{\cos ^4}\alpha \sin \alpha – 10{\cos ^2}\alpha {\sin ^3}\alpha + {\sin ^5}\alpha \) A1
\(\sin \alpha \ne 0 \Rightarrow 0 = 5{(1 – {\sin ^2}\alpha )^2} – 10(1 – {\sin ^2}\alpha ){\sin ^2}\alpha + {\sin ^4}\alpha \) M1
Note: Award M1 for replacing \({\cos ^2}\alpha \).
\(0 = 5(1 – 2{\sin ^2}\alpha + {\sin ^4}\alpha ) – 10{\sin ^2}\alpha + 10{\sin ^4}\alpha + {\sin ^4}\alpha \) A1
Note: Award A1 for any correct simplification.
so \(16{\sin ^4}\alpha – 20{\sin ^2}\alpha + 5 = 0\) AG
[4 marks]
\({\sin ^2}\alpha = \frac{{20 \pm \sqrt {400 – 320} }}{{32}}\) M1A1
\(\sin \alpha = \pm \sqrt {\frac{{20 \pm \sqrt {80} }}{{32}}} \)
\(\sin \alpha = \frac{{ \pm \sqrt {10 \pm 2\sqrt 5 } }}{4}\) A1
Note: Award A1 regardless of signs. Accept equivalent forms with integral denominator, simplification may be seen later.
as \(72 > 60\), \(\sin 72 > \frac{{\sqrt 3 }}{2} = 0.866 \ldots \) we have to take both positive signs (or equivalent argument) R1
Note: Allow verification of correct signs with calculator if clearly stated
\(\sin 72 = \frac{{\sqrt {10 + 2\sqrt 5 } }}{4}\) A1
[5 marks]
Total [19 marks]
Question
a.In triangle \(ABC\),
\(3\sin B + 4\cos C = 6\) and
\(4\sin C + 3\cos B = 1\).
Show that \(\sin (B + C) = \frac{1}{2}\).[6]
Show that Robert’s conjecture is incorrect by proving that \({\rm{C\hat AB}}\) has only one possible value.[5]
▶️Answer/Explanation
Markscheme
METHOD 1
squaring both equations M1
\(9{\sin ^2}B + 24\sin B\cos C + 16{\cos ^2}C = 36\) (A1)
\(9{\cos ^2}B + 24\cos B\sin C + 16{\sin ^2}C = 1\) (A1)
adding the equations and using \({\cos ^2}\theta + {\sin ^2}\theta = 1\) to obtain \(9 + 24\sin (B + C) + 16 = 37\) M1
\(24(\sin B\cos C + \cos B\sin C) = 12\) A1
\(24\sin (B + C) = 12\) (A1)
\(\sin (B + C) = \frac{1}{2}\) AG
METHOD 2
substituting for \(\sin B\) and \(\cos B\) to obtain
\(\sin (B + C) = \left( {\frac{{6 – 4\cos C}}{3}} \right)\cos C + \left( {\frac{{1 – 4\sin C}}{3}} \right)\sin C\) M1
\( = \frac{{6\cos C + \sin C – 4}}{3}\;\;\;\)(or equivalent) A1
substituting for \(\sin C\) and \(\cos C\) to obtain
\(\sin (B + C) = \sin B\left( {\frac{{6 – 3\sin B}}{4}} \right) + \cos B\left( {\frac{{1 – 3\cos B}}{4}} \right)\) M1
\( = \frac{{\cos B + 6\sin B – 3}}{4}\;\;\;\)(or equivalent) A1
Adding the two equations for \(\sin (B + C)\):
\(2\sin (B + C) = \frac{{(18\sin B + 24\cos C) + (4\sin C + 3\cos B) – 25}}{{12}}\) A1
\(\sin (B + C) = \frac{{36 + 1 – 25}}{{24}}\) (A1)
\(\sin (B + C) = \frac{1}{2}\) AG
METHOD 3
substituting \(\sin B\) and \(\sin C\) to obtain
\(\sin (B + C) = \left( {\frac{{6 – 4\cos C}}{3}} \right)\cos C + \cos B\left( {\frac{{1 – 3\cos B}}{4}} \right)\) M1
substituting for \(\cos B\) and \(\cos B\) to obtain
\(\sin (B + C) = \sin B\left( {\frac{{6 – 3\sin B}}{4}} \right) + \left( {\frac{{1 – 4\sin C}}{3}} \right)\sin C\) M1
Adding the two equations for \(\sin (B + C)\):
\(2\sin (B + C) = \frac{{6\cos C + \sin C – 4}}{3} + \frac{{6\sin B + \cos B – 3}}{4}\;\;\;\)(or equivalent) A1A1
\(2\sin (B + C) = \frac{{(18\sin B + 24\cos C) + (4\sin C + 3\cos B) – 25}}{{12}}\) A1
\(\sin (B + C) = \frac{{36 + 1 – 25}}{{24}}\) (A1)
\(\sin (B + C) = \frac{1}{2}\) AG
[6 marks]
\(\sin A = \sin \left( {180^\circ – (B + C)} \right)\) so \(\sin A = \sin (B + C)\) R1
\(\sin (B + C) = \frac{1}{2} \Rightarrow \sin A = \frac{1}{2}\) A1
\( \Rightarrow A = 30^\circ \) or \(A = 150^\circ \) A1
if \(A = 150^\circ \), then \(B < 30^\circ \) R1
for example, \(3\sin B + 4\cos C < \frac{3}{2} + 4 < 6\), ie a contradiction R1
only one possible value \((A = 30^\circ )\) AG
[5 marks]
Total [11 marks]
