Question
Given that \(\cos A = \frac{1}{3}\) and \(0 \le A \le \frac{\pi }{2}\) , find \(\cos 2A\) .
Given that \(\sin B = \frac{2}{3}\) and \(\frac{\pi }{2} \le B \le \pi \) , find \(\cos B\) .
Answer/Explanation
Markscheme
evidence of choosing the formula \(\cos 2A = 2{\cos ^2}A – 1\) (M1)
Note: If they choose another correct formula, do not award the M1 unless there is evidence of finding \({\sin ^2}A = 1 – \frac{1}{9}\)
correct substitution A1
e.g.\(\cos 2A = {\left( {\frac{1}{3}} \right)^2} – \frac{8}{9}\) , \(\cos 2A = 2 \times {\left( {\frac{1}{3}} \right)^2} – 1\)
\(\cos 2A = – \frac{7}{9}\) A1 N2
[3 marks]
METHOD 1
evidence of using \({\sin ^2}B + {\cos ^2}B = 1\) (M1)
e.g. \({\left( {\frac{2}{3}} \right)^2} + {\cos ^2}B = 1\) , \(\sqrt {\frac{5}{9}} \) (seen anywhere),
\(\cos B = \pm \sqrt {\frac{5}{9}} \) \(\left( { = \pm \frac{{\sqrt 5 }}{3}} \right)\) (A1)
\(\cos B = – \sqrt {\frac{5}{9}} \) \(\left( { = – \frac{{\sqrt 5 }}{3}} \right)\) A1 N2
METHOD 2
diagram M1
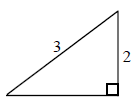
for finding third side equals \(\sqrt 5 \) (A1)
\(\cos B = – \frac{{\sqrt 5 }}{3}\) A1 N2
[3 marks]
Question
Let \(f(x) = {\sin ^3}x + {\cos ^3}x\tan x,\frac{\pi }{2} < x < \pi \) .
Show that \(f(x) = \sin x\) .
Let \(\sin x = \frac{2}{3}\) . Show that \(f(2x) = – \frac{{4\sqrt 5 }}{9}\) .
Answer/Explanation
Markscheme
changing \(\tan x\) into \(\frac{{\sin x}}{{\cos x}}\) A1
e.g. \({\sin ^3}x + {\cos ^3}x\frac{{\sin x}}{{\cos x}}\)
simplifying A1
e.g \(\sin x({\sin ^2}x + {\cos ^2}x)\) , \({\sin ^3}x + \sin x – {\sin ^3}x\)
\(f(x) = \sin x\) AG N0
[2 marks]
recognizing \(f(2x) = \sin 2x\) , seen anywhere (A1)
evidence of using double angle identity \(\sin (2x) = 2\sin x\cos x\) , seen anywhere (M1)
evidence of using Pythagoras with \(\sin x = \frac{2}{3}\) M1
e.g. sketch of right triangle, \({\sin ^2}x + {\cos ^2}x = 1\)
\(\cos x = – \frac{{\sqrt 5 }}{3}\) (accept \(\frac{{\sqrt 5 }}{3}\) ) (A1)
\(f(2x) = 2\left( {\frac{2}{3}} \right)\left( { – \frac{{\sqrt 5 }}{3}} \right)\) A1
\(f(2x) = – \frac{{4\sqrt 5 }}{9}\) AG N0
[5 marks]
Question
The vertices of the triangle PQR are defined by the position vectors
\(\overrightarrow {{\rm{OP}}} = \left( {\begin{array}{*{20}{c}}
4\\
{ – 3}\\
1
\end{array}} \right)\) , \(\overrightarrow {{\rm{OQ}}} = \left( {\begin{array}{*{20}{c}}
3\\
{ – 1}\\
2
\end{array}} \right)\) and \(\overrightarrow {{\rm{OR}}} = \left( {\begin{array}{*{20}{c}}
6\\
{ – 1}\\
5
\end{array}} \right)\) .
Find
(i) \(\overrightarrow {{\rm{PQ}}} \) ;
(ii) \(\overrightarrow {{\rm{PR}}} \) .
Show that \(\cos {\rm{R}}\widehat {\rm{P}}{\rm{Q}} = \frac{1}{2}\) .
(i) Find \({\rm{sinR}}\widehat {\rm{P}}{\rm{Q}}\) .
(ii) Hence, find the area of triangle PQR, giving your answer in the form \(a\sqrt 3 \) .
Answer/Explanation
Markscheme
(i) evidence of approach (M1)
e.g. \(\overrightarrow {{\rm{PQ}}} = \overrightarrow {{\rm{PO}}} + \overrightarrow {{\rm{OQ}}} \) , \({\rm{Q}} – {\rm{P}}\)
\(\overrightarrow {{\rm{PQ}}} = \left( {\begin{array}{*{20}{c}}
{ – 1}\\
2\\
1
\end{array}} \right)\) A1 N2
(ii) \(\overrightarrow {{\rm{PR}}} = \left( {\begin{array}{*{20}{c}}
2\\
2\\
4
\end{array}} \right)\) A1 N1
[3 marks]
METHOD 1
choosing correct vectors \(\overrightarrow {{\rm{PQ}}} \) and \(\overrightarrow {{\rm{PR}}} \) (A1)(A1)
finding \(\overrightarrow {{\rm{PQ}}} \bullet \overrightarrow {{\rm{PR}}} \) , \(\left| {\overrightarrow {{\rm{PQ}}} } \right|\) , \(\left| {\overrightarrow {{\rm{PR}}} } \right|\) (A1) (A1)(A1)
\(\overrightarrow {{\rm{PQ}}} \bullet \overrightarrow {{\rm{PR}}} = – 2 + 4 + 4( = 6)\)
\(\left| {\overrightarrow {{\rm{PQ}}} } \right| = \sqrt {{{( – 1)}^2} + {2^2} + {1^2}} \) \(\left( { = \sqrt 6 } \right)\) , \(\left| {\overrightarrow {{\rm{PR}}} } \right| = \sqrt {{2^2} + {2^2} + {4^2}} \) \(\left( { = \sqrt {24} } \right)\)
substituting into formula for angle between two vectors M1
e.g. \(\cos {\rm{R}}\widehat {\rm{P}}{\rm{Q}} = \frac{6}{{\sqrt 6 \times \sqrt {24} }}\)
simplifying to expression clearly leading to \(\frac{1}{2}\) A1
e.g. \(\frac{6}{{\sqrt 6 \times 2\sqrt 6 }}\) , \(\frac{6}{{\sqrt {144} }}\) , \(\frac{6}{{12}}\)
\(\cos {\rm{R}}\widehat {\rm{P}}{\rm{Q}} = \frac{1}{2}\) AG N0
METHOD 2
evidence of choosing cosine rule (seen anywhere) (M1)
\(\overrightarrow {{\rm{QR}}} = \left( {\begin{array}{*{20}{c}}
3\\
0\\
3
\end{array}} \right)\) A1
\(\left| {\overrightarrow {{\rm{QR}}} } \right| = \sqrt {18} \) , \(\left| {\overrightarrow {{\rm{PQ}}} } \right| = \sqrt 6 \) and \(\left| {\overrightarrow {{\rm{PR}}} } \right| = \sqrt {24} \) (A1)(A1)(A1)
\(\cos {\rm{R}}\widehat {\rm{P}}{\rm{Q}} = \frac{{{{\left( {\sqrt 6 } \right)}^2} + {{\left( {\sqrt {24} } \right)}^2} – {{\left( {\sqrt {18} } \right)}^2}}}{{2\sqrt 6 \times \sqrt {24} }}\) A1
\(\cos {\rm{R}}\widehat {\rm{P}}{\rm{Q}} = \frac{{6 + 24 – 18}}{{24}}\) \(\left( { = \frac{{12}}{{24}}} \right)\) A1
\(\cos {\rm{R}}\widehat {\rm{P}}{\rm{Q}} = \frac{1}{2}\) AG N0
[7 marks]
(i) METHOD 1
evidence of appropriate approach (M1)
e.g. using \({\rm{si}}{{\rm{n}}^{\rm{2}}}{\rm{R}}\widehat {\rm{P}}{\rm{Q + co}}{{\rm{s}}^{\rm{2}}}{\rm{R}}\widehat {\rm{P}}{\rm{Q}} = 1\) , diagram
substituting correctly (A1)
e.g. \({\rm{sinR}}\widehat {\rm{P}}{\rm{Q}} = \sqrt {1 – {{\left( {\frac{1}{2}} \right)}^2}} \)
\({\rm{sinR}}\widehat {\rm{P}}{\rm{Q}} = \sqrt {\frac{3}{4}} \) \(\left( { = \frac{{\sqrt 3 }}{2}} \right)\) A1 N3
METHOD 2
since \(\cos \widehat {\rm{P}} = \frac{1}{2}\) , \(\widehat {\rm{P}} = 60^\circ \) (A1)
evidence of approach
e.g. drawing a right triangle, finding the missing side (A1)
\(\sin \widehat {\rm{P}} = \frac{{\sqrt 3 }}{2}\) A1 N3
(ii) evidence of appropriate approach (M1)
e.g. attempt to substitute into \(\frac{1}{2}ab\sin C\)
correct substitution
e.g. area \( = \frac{1}{2}\sqrt 6 \times \sqrt {24} \times \frac{{\sqrt 3 }}{2}\) A1
area \( = 3\sqrt 3 \) A1 N2
[6 marks]
Question
Let \(\sin \theta = \frac{2}{{\sqrt {13} }}\) , where \(\frac{\pi }{2} < \theta < \pi \) .
Find \(\cos \theta \) .
Find \(\tan 2\theta \) .
Answer/Explanation
Markscheme
METHOD 1
evidence of choosing \({\sin ^2}\theta + {\cos ^2}\theta = 1\) (M1)
correct working (A1)
e.g. \({\cos ^2}\theta = \frac{9}{{13}}\) , \(\cos \theta = \pm \frac{3}{{\sqrt {13} }}\) , \(\cos \theta = \sqrt {\frac{9}{{13}}} \)
\(\cos \theta = – \frac{3}{{\sqrt {13} }}\) A1 N2
Note: If no working shown, award N1 for \(\frac{3}{{\sqrt {13} }}\) .
METHOD 2
approach involving Pythagoras’ theorem (M1)
e.g. \({2^2} + {x^2} = 13\) ,
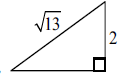
finding third side equals 3 (A1)
\(\cos \theta = – \frac{3}{{\sqrt {13} }}\) A1 N2
Note: If no working shown, award N1 for \(\frac{3}{{\sqrt {13} }}\) .
[3 marks]
correct substitution into \(\sin 2\theta \) (seen anywhere) (A1)
e.g. \(2\left( {\frac{2}{{\sqrt {13} }}} \right)\left( { – \frac{3}{{\sqrt {13} }}} \right)\)
correct substitution into \(\cos 2\theta \) (seen anywhere) (A1)
e.g. \({\left( { – \frac{3}{{\sqrt {13} }}} \right)^2} – {\left( {\frac{2}{{\sqrt {13} }}} \right)^2}\) , \(2{\left( { – \frac{3}{{\sqrt {13} }}} \right)^2} – 1\) , \(1 – 2{\left( {\frac{2}{{\sqrt {13} }}} \right)^2}\)
valid attempt to find \(\tan 2\theta \) (M1)
e.g. \(\frac{{2\left( {\frac{2}{{\sqrt {13} }}} \right)\left( { – \frac{3}{{\sqrt {13} }}} \right)}}{{{{\left( { – \frac{3}{{\sqrt {13} }}} \right)}^2} – {{\left( {\frac{2}{{\sqrt {13} }}} \right)}^2}}}\) , \(\frac{{2\left( { – \frac{2}{3}} \right)}}{{1 – {{\left( { – \frac{2}{3}} \right)}^2}}}\)
correct working A1
e.g. \(\frac{{\frac{{(2)(2)( – 3)}}{{13}}}}{{\frac{9}{{13}} – \frac{4}{{13}}}}\) , \(\frac{{ – \frac{{12}}{{{{\left( {\sqrt {13} } \right)}^2}}}}}{{\frac{{18}}{{13}} – 1}}\) , \(\frac{{ – \frac{{12}}{{13}}}}{{\frac{5}{{13}}}}\)
\(\tan 2\theta = – \frac{{12}}{5}\) A1 N4
Note: If students find answers for \(\cos \theta \) which are not in the range \([ – 1{\text{, }}1]\), award full FT in (b) for correct FT working shown.
[5 marks]
Question
Let \(f(x) = {(\sin x + \cos x)^2}\) .
Show that \(f(x)\) can be expressed as \(1 + \sin 2x\) .
The graph of f is shown below for \(0 \le x \le 2\pi \) .
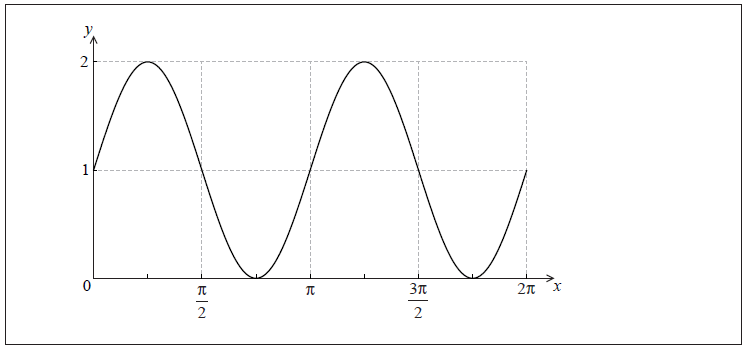
Let \(g(x) = 1 + \cos x\) . On the same set of axes, sketch the graph of g for \(0 \le x \le 2\pi \) .
The graph of g can be obtained from the graph of f under a horizontal stretch of scale factor p followed by a translation by the vector \(\left( {\begin{array}{*{20}{c}}
k\\
0
\end{array}} \right)\) .
Write down the value of p and a possible value of k .
Answer/Explanation
Markscheme
attempt to expand (M1)
e.g. \((\sin x + \cos x)(\sin x + \cos x)\) ; at least 3 terms
correct expansion A1
e.g. \({\sin ^2}x + 2\sin x\cos x + {\cos ^2}x\)
\(f(x) = 1 + \sin 2x\) AG N0
[2 marks]
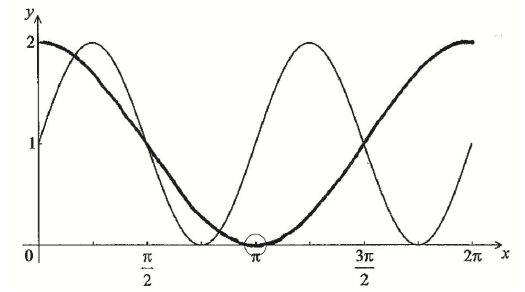A1A1 N2
Note: Award A1 for correct sinusoidal shape with period \(2\pi \) and range \([0{\text{, }}2]\), A1 for minimum in circle.
\(p = 2\) , \(k = – \frac{\pi }{2}\) A1A1 N2
[2 marks]
Question
Let \(\sin {100^ \circ } = m\). Find an expression for \(\cos {100^ \circ }\) in terms of m.
Let \(\sin {100^ \circ } = m\) . Find an expression for \(\tan {100^ \circ }\) in terms of m.
Let \(\sin {100^ \circ } = m\). Find an expression for \(\sin {200^ \circ }\) in terms of m.
Answer/Explanation
Markscheme
Note: All answers must be given in terms of m. If a candidate makes an error that means there is no m in their answer, do not award the final A1FT mark.
METHOD 1
valid approach involving Pythagoras (M1)
e.g. \({\sin ^2}x + {\cos ^2}x = 1\) , labelled diagram 
correct working (may be on diagram) (A1)
e.g. \({m^2} + {(\cos 100)^2} = 1\) , \(\sqrt {1 – {m^2}} \)
\(\cos 100 = – \sqrt {1 – {m^2}} \) A1 N2
[3 marks]
METHOD 2
valid approach involving tan identity (M1)
e.g. \(\tan = \frac{{\sin }}{{\cos }}\)
correct working (A1)
e.g. \(\cos 100 = \frac{{\sin 100}}{{\tan 100}}\)
\(\cos 100 = \frac{m}{{\tan 100}}\) A1 N2
[3 marks]
METHOD 1
\(\tan 100 = – \frac{m}{{\sqrt {1 – {m^2}} }}\) (accept \(\frac{m}{{ – \sqrt {1 – {m^2}} }}\)) A1 N1
[1 mark]
METHOD 2
\(\tan 100 = \frac{m}{{\cos 100}}\) A1 N1
[1 mark]
METHOD 1
valid approach involving double angle formula (M1)
e.g. \(\sin 2\theta = 2\sin \theta cos\theta \)
\(\sin 200 = – 2m\sqrt {1 – {m^2}} \) (accept \(2m\left( { – \sqrt {1 – {m^2}} } \right)\)) A1 N2
Note: If candidates find \(\cos 100 = \sqrt {1 – {m^2}} \) , award full FT in parts (b) and (c), even though the values may not have appropriate signs for the angles.
[2 marks]
METHOD 2
valid approach involving double angle formula (M1)
e.g. \(\sin 2\theta = 2\sin \theta \cos \theta \) , \(2m \times \frac{m}{{\tan 100}}\)
\(\sin 200 = \frac{{2{m^2}}}{{\tan 100}}( = 2m\cos 100)\) A1 N2
[2 marks]
Question
The following diagram shows a right-angled triangle, \(\rm{ABC}\), where \(\sin \rm{A} = \frac{5}{{13}}\).
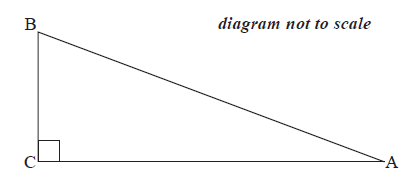
Show that \(\cos A = \frac{{12}}{{13}}\).
Find \(\cos 2A\).
Answer/Explanation
Markscheme
METHOD 1
approach involving Pythagoras’ theorem (M1)
eg \({5^2} + {x^2} = {13^2}\), labelling correct sides on triangle
finding third side is 12 (may be seen on diagram) A1
\(\cos A = \frac{{12}}{{13}}\) AG N0
METHOD 2
approach involving \({\sin ^2}\theta + {\cos ^2}\theta = 1\) (M1)
eg \({\left( {\frac{5}{{13}}} \right)^2} + {\cos ^2}\theta = 1,{\text{ }}{x^2} + \frac{{25}}{{169}} = 1\)
correct working A1
eg \({\cos ^2}\theta = \frac{{144}}{{169}}\)
\(\cos A = \frac{{12}}{{13}}\) AG N0
[2 marks]
correct substitution into \(\cos 2\theta \) (A1)
eg \(1 – 2{\left( {\frac{5}{{13}}} \right)^2},{\text{ }}2{\left( {\frac{{12}}{{13}}} \right)^2} – 1,{\text{ }}{\left( {\frac{{12}}{{13}}} \right)^2} – {\left( {\frac{5}{{13}}} \right)^2}\)
correct working (A1)
eg \(1 – \frac{{50}}{{169}},{\text{ }}\frac{{288}}{{169}} – 1,{\text{ }}\frac{{144}}{{169}} – \frac{{25}}{{169}}\)
\(\cos 2A = \frac{{119}}{{169}}\) A1 N2
[3 marks]