Question
The following graph shows the depth of water, y metres , at a point P, during one day. The time t is given in hours, from midnight to noon.
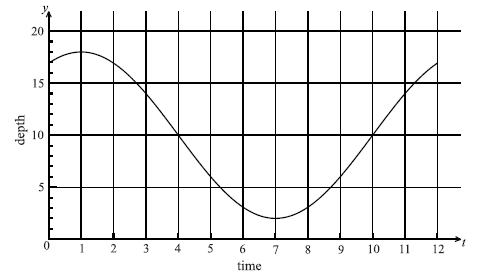
Use the graph to write down an estimate of the value of t when
(i) the depth of water is minimum;
(ii) the depth of water is maximum;
(iii) the depth of the water is increasing most rapidly.
The depth of water can be modelled by the function \(y = \cos A(B(t – 1)) + C\) .
(i) Show that \(A = 8\) .
(ii) Write down the value of C.
(iii) Find the value of B.
A sailor knows that he cannot sail past P when the depth of the water is less than 12 m . Calculate the values of t between which he cannot sail past P.
Answer/Explanation
Markscheme
(i) 7 A1 N1
(ii) 1 A1 N1
(iii) 10 A1 N1
[3 marks]
(i) evidence of appropriate approach M1
e.g. \(A = \frac{{18 – 2}}{2}\)
\(A = 8\) AG N0
(ii) \(C = 10\) A2 N2
(iii) METHOD 1
\({\text{period}} = 12\) (A1)
evidence of using \(B \times {\rm{period}} = 2\pi \) (accept \(360^\circ \) ) (M1)
e.g. \(12 = \frac{{2\pi }}{B}\)
\(B = \frac{\pi }{6}\) (accept 0.524 or 30) A1 N3
METHOD 2
evidence of substituting (M1)
e.g. \(10 = 8\cos 3B + 10\)
simplifying (A1)
e.g. \(\cos 3B = 0\) \(\left( {3B = \frac{\pi }{2}} \right)\)
\(B = \frac{\pi }{6}\) (accept 0.524 or 30) A1 N3
[6 marks]
correct answers A1A1
e.g. \(t = 3.52\) , \(t = 10.5\) , between 03:31 and 10:29 (accept 10:30) N2
[2 marks]
Question
Let \(f(x) = \frac{{3x}}{2} + 1\) , \(g(x) = 4\cos \left( {\frac{x}{3}} \right) – 1\) . Let \(h(x) = (g \circ f)(x)\) .
Find an expression for \(h(x)\) .
Write down the period of \(h\) .
Write down the range of \(h\) .
Answer/Explanation
Markscheme
attempt to form any composition (even if order is reversed) (M1)
correct composition \(h(x) = g\left( {\frac{{3x}}{2} + 1} \right)\) (A1)
\(h(x) = 4\cos \left( {\frac{{\frac{{3x}}{2} + 1}}{3}} \right) – 1\) \(\left( {4\cos \left( {\frac{1}{2}x + \frac{1}{3}} \right) – 1,4\cos \left( {\frac{{3x + 2}}{6}} \right) – 1} \right)\) A1 N3
[3 marks]
period is \(4\pi (12.6)\) A1 N1
[1 mark]
range is \( – 5 \le h(x) \le 3\) \(\left( {\left[ { – 5,3} \right]} \right)\) A1A1 N2
[2 marks]
Question
Let \(f(x) = 5\cos \frac{\pi }{4}x\) and \(g(x) = – 0.5{x^2} + 5x – 8\) for \(0 \le x \le 9\) .
On the same diagram, sketch the graphs of f and g .
Consider the graph of \(f\) . Write down
(i) the x-intercept that lies between \(x = 0\) and \(x = 3\) ;
(ii) the period;
(iii) the amplitude.
Consider the graph of g . Write down
(i) the two x-intercepts;
(ii) the equation of the axis of symmetry.
Let R be the region enclosed by the graphs of f and g . Find the area of R.
Answer/Explanation
Markscheme
 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for f being of sinusoidal shape, with 2 maxima and one minimum, A1 for g being a parabola opening down, A1 for two intersection points in approximately correct position.
[3 marks]
(i) \((2{\text{, }}0)\) (accept \(x = 2\) ) A1 N1
(ii) \({\text{period}} = 8\) A2 N2
(iii) \({\text{amplitude}} = 5\) A1 N1
[4 marks]
(i) \((2{\text{, }}0)\) , \((8{\text{, }}0)\) (accept \(x = 2\) , \(x = 8\) ) A1A1 N1N1
(ii) \(x = 5\) (must be an equation) A1 N1
[3 marks]
METHOD 1
intersect when \(x = 2\) and \(x = 6.79\) (may be seen as limits of integration) A1A1
evidence of approach (M1)
e.g. \(\int {g – f} \) , \(\int {f(x){\rm{d}}x – \int {g(x){\rm{d}}x}}\) , \(\int_2^{6.79} {\left( {( – 0.5{x^2} + 5x – 8) – \left( {5\cos \frac{\pi }{4}x} \right)} \right)}\)
\({\text{area}} = 27.6\) A2 N3
METHOD 2
intersect when \(x = 2\) and \(x = 6.79\) (seen anywhere) A1A1
evidence of approach using a sketch of g and f , or \(g – f\) . (M1)
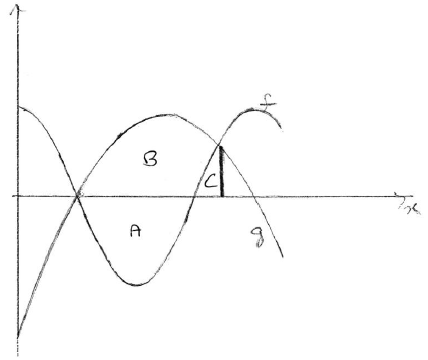
e.g. area = \(A + B – C\) , \(12.7324 + 16.0938 – 1.18129 \ldots \)
\({\text{area}} = 27.6\) A2 N3
[5 marks]
Question
Let \(f(x) = a\cos (b(x – c))\) . The diagram below shows part of the graph of f , for \(0 \le x \le 10\) .
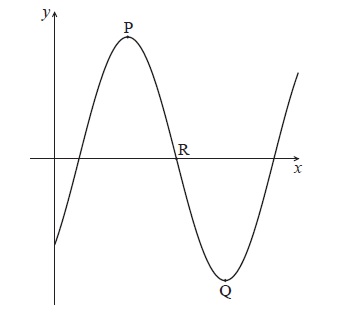
The graph has a local maximum at P(3, 5) , a local minimum at Q(7, − 5) , and crosses the x-axis at R.
Write down the value of
(i) \(a\) ;
(ii) \(c\) .
Find the value of b .
Find the x-coordinate of R.
Answer/Explanation
Markscheme
(i) \(a = 5\) (accept \( – 5\) ) A1 N1
(ii) \(c = 3\) (accept \(c = 7\) , if \(a = – 5\) ) A1 N1
Note: Accept other correct values of c, such as 11, \( – 5\), etc.
[2 marks]
attempt to find period (M1)
e.g. 8 , \(b = \frac{{2\pi }}{{{\rm{period}}}}\)
\(0.785398 \ldots \)
\(b = \frac{{2\pi }}{8}\) (exact), \(\frac{\pi }{4}\) , 0.785 [\(0.785{\text{, }}0.786\)] (do not accept 45) A1 N2
[2 marks]
valid approach (M1)
e.g. \(f(x) = 0\) , symmetry of curve
\(x = 5\) (accept \((5{\text{ ,}}0))\) A1 N2
[2 marks]
Question
A Ferris wheel with diameter \(122\) metres rotates clockwise at a constant speed. The wheel completes \(2.4\) rotations every hour. The bottom of the wheel is \(13\) metres above the ground.
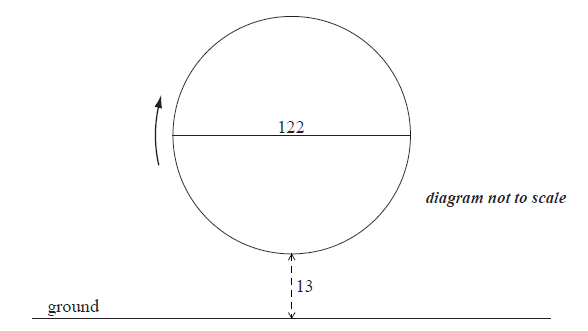
A seat starts at the bottom of the wheel.
After t minutes, the height \(h\) metres above the ground of the seat is given by\[h = 74 + a\cos bt {\rm{ .}}\]
Find the maximum height above the ground of the seat.
(i) Show that the period of \(h\) is \(25\) minutes.
(ii) Write down the exact value of \(b\) .
(b) (i) Show that the period of \(h\) is \(25\) minutes.
(ii) Write down the exact value of \(b\) .
(c) Find the value of \(a\) .
(d) Sketch the graph of \(h\) , for \(0 \le t \le 50\) .
Find the value of \(a\) .
Sketch the graph of \(h\) , for \(0 \le t \le 50\) .
In one rotation of the wheel, find the probability that a randomly selected seat is at least \(105\) metres above the ground.
Answer/Explanation
Markscheme
valid approach (M1)
eg \(13 + {\rm{diameter}}\) , \(13 + 122\)
maximum height \( = 135\) (m) A1 N2
[2 marks]
(i) period \( = \frac{{60}}{{2.4}}\) A1
period \( = 25\) minutes AG N0
(ii) \(b = \frac{{2\pi }}{{25}}\) \(( = 0.08\pi )\) A1 N1
[2 marks]
(a) (i) period \( = \frac{{60}}{{2.4}}\) A1
period \( = 25\) minutes AG N0
(ii) \(b = \frac{{2\pi }}{{25}}\) \(( = 0.08\pi )\) A1 N1
[2 marks]
(b) METHOD 1
valid approach (M1)
eg \({\rm{max}} – 74\) , \(\left| a \right| = \frac{{135 – 13}}{2}\) , \(74 – 13\)
\(\left| a \right| = 61\) (accept \(a = 61\) ) (A1)
\(a = – 61\) A1 N2
METHOD 2
attempt to substitute valid point into equation for h (M1)
eg \(135 = 74 + a\cos \left( {\frac{{2\pi \times 12.5}}{{25}}} \right)\)
correct equation (A1)
eg \(135 = 74 + a\cos (\pi )\) , \(13 = 74 + a\)
\(a = – 61\) A1 N2
[3 marks]
(c)
A1A1A1A1 N4
Note: Award A1 for approximately correct domain, A1 for approximately correct range,
A1 for approximately correct sinusoidal shape with \(2\) cycles.
Only if this last A1 awarded, award A1 for max/min in approximately correct positions.
[4 marks]
Total [9 marks]
METHOD 1
valid approach (M1)
eg \({\rm{max}} – 74\) , \(\left| a \right| = \frac{{135 – 13}}{2}\) , \(74 – 13\)
\(\left| a \right| = 61\) (accept \(a = 61\) ) (A1)
\(a = – 61\) A1 N2
METHOD 2
attempt to substitute valid point into equation for h (M1)
eg \(135 = 74 + a\cos \left( {\frac{{2\pi \times 12.5}}{{25}}} \right)\)
correct equation (A1)
eg \(135 = 74 + a\cos (\pi )\) , \(13 = 74 + a\)
\(a = – 61\) A1 N2
[3 marks]
A1A1A1A1 N4
Note: Award A1 for approximately correct domain, A1 for approximately correct range,
A1 for approximately correct sinusoidal shape with \(2\) cycles.
Only if this last A1 awarded, award A1 for max/min in approximately correct positions.
[4 marks]
setting up inequality (accept equation) (M1)
eg \(h > 105\) , \(105 = 74 + a\cos bt\) , sketch of graph with line \(y = 105\)
any two correct values for t (seen anywhere) A1A1
eg \(t = 8.371 \ldots \) , \(t = 16.628 \ldots \) , \(t = 33.371 \ldots \) , \(t = 41.628 \ldots \)
valid approach M1
eg \(\frac{{16.628 – 8.371}}{{25}}\) , \(\frac{{{t_1} – {t_2}}}{{25}}\) , \(\frac{{2 \times 8.257}}{{50}}\) , \(\frac{{2(12.5 – 8.371)}}{{25}}\)
\(p = 0.330\) A1 N2
[5 marks]
Question
The population of deer in an enclosed game reserve is modelled by the function \(P(t) = 210\sin (0.5t – 2.6) + 990\), where \(t\) is in months, and \(t = 1\) corresponds to 1 January 2014.
Find the number of deer in the reserve on 1 May 2014.
Find the rate of change of the deer population on 1 May 2014.
Interpret the answer to part (i) with reference to the deer population size on 1 May 2014.
Answer/Explanation
Markscheme
\(t = 5\) (A1)
correct substitution into formula (A1)
eg \(210\sin (0.5 \times 5 – 2.6) + 990,{\text{ }}P(5)\)
\(969.034982 \ldots \)
969 (deer) (must be an integer) A1 N3
[3 marks]
evidence of considering derivative (M1)
eg \(P’\)
\(104.475\)
\(104\) (deer per month) A1 N2
[2 marks]
(the deer population size is) increasing A1 N1
[1 mark]
Question
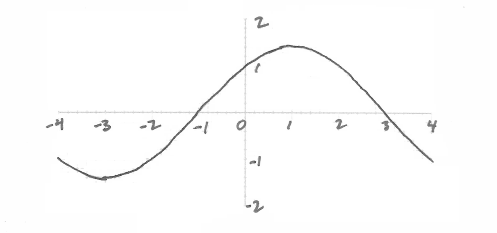
Let \(f(x) = \cos \left( {\frac{\pi }{4}x} \right) + \sin \left( {\frac{\pi }{4}x} \right),{\text{ for }} – 4 \leqslant x \leqslant 4.\)
Sketch the graph of \(f\).
Find the values of \(x\) where the function is decreasing.
The function \(f\) can also be written in the form \(f(x) = a\sin \left( {\frac{\pi }{4}(x + c)} \right)\), where \(a \in \mathbb{R}\), and \(0 \leqslant c \leqslant 2\). Find the value of \(a\);
The function \(f\) can also be written in the form \(f(x) = a\sin \left( {\frac{\pi }{4}(x + c)} \right)\), where \(a \in \mathbb{R}\), and \(0 \leqslant c \leqslant 2\). Find the value of \(c\).
Answer/Explanation
Markscheme
 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for approximately correct sinusoidal shape.
Only if this A1 is awarded, award the following:
A1 for correct domain,
A1 for approximately correct range.
[3 marks]
recognizes decreasing to the left of minimum or right of maximum,
eg \(f'(x) < 0\) (R1)
x-values of minimum and maximum (may be seen on sketch in part (a)) (A1)(A1)
eg \(x = – 3,{\text{ (1, 1.4)}}\)
two correct intervals A1A1 N5
eg \( – 4 < x < – 3,{\text{ }}1 \leqslant x \leqslant 4;{\text{ }}x < – 3,{\text{ }}x \geqslant 1\)
[5 marks]
recognizes that \(a\) is found from amplitude of wave (R1)
y-value of minimum or maximum (A1)
eg (−3, −1.41) , (1, 1.41)
\(a = 1.41421\)
\(a = \sqrt 2 {\text{, (exact), 1.41,}}\) A1 N3
[3 marks]
METHOD 1
recognize that shift for sine is found at x-intercept (R1)
attempt to find x-intercept (M1)
eg \(\cos \left( {\frac{\pi }{4}x} \right) + \sin \left( {\frac{\pi }{4}x} \right) = 0,{\text{ }}x = 3 + 4k,{\text{ }}k \in \mathbb{Z}\)
\(x = – 1\) (A1)
\(c = 1\) A1 N4
METHOD 2
attempt to use a coordinate to make an equation (R1)
eg \(\sqrt 2 \sin \left( {\frac{\pi }{4}c} \right) = 1,{\text{ }}\sqrt 2 \sin \left( {\frac{\pi }{4}(3 – c)} \right) = 0\)
attempt to solve resulting equation (M1)
eg sketch, \(x = 3 + 4k,{\text{ }}k \in \mathbb{Z}\)
\(x = – 1\) (A1)
\(c = 1\) A1 N4
[4 marks]
Question
Let \(f(x) = p\cos \left( {q(x + r)} \right) + 10\), for \(0 \leqslant x \leqslant 20\). The following diagram shows the graph of \(f\).
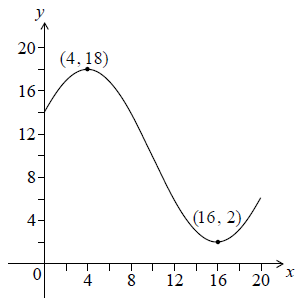
The graph has a maximum at \((4, 18)\) and a minimum at \((16, 2)\).
Write down the value of \(r\).
Find \(p\).
Find \(q\).
Solve \(f(x) = 7\).
Answer/Explanation
Markscheme
\(r = – 4\) A2 N2
Note: Award A1 for \(r = 4\).
[2 marks]
evidence of valid approach (M1)
eg \(\frac{{\max y{\text{ value — }}y{\text{ value}}}}{2}\), distance from \(y = 10\)
\(p = 8\) A1 N2
[2 marks]
valid approach (M1)
eg period is \(24\), \(\frac{{360}}{{24}}\), substitute a point into their \(f(x)\)
\(q = \frac{{2\pi }}{{24}}\left( {\frac{\pi }{{12}},{\text{ exact}}} \right)\), \(0.262\) (do not accept degrees) A1 N2
[2 marks]
valid approach (M1)
eg line on graph at \(y = 7,{\text{ }}8\cos \left( {\frac{{2\pi }}{{24}}(x – 4)} \right) + 10 = 7\)
\(x = 11.46828\)
\(x = 11.5\) (accept \((11.5, 7)\)) A1 N2
[2 marks]
Note: Do not award the final A1 if additional values are given. If an incorrect value of \(q\) leads to multiple solutions, award the final A1 only if all solutions within the domain are given.
Question
The following diagram shows part of the graph of \(y = p\sin (qx) + r\).
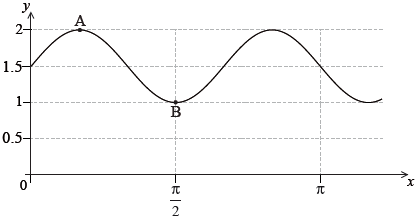
The point \({\text{A}}\left( {\frac{\pi }{6},{\text{ }}2} \right)\) is a maximum point and the point \({\text{B}}\left( {\frac{\pi }{6},{\text{ }}1} \right)\) is a minimum point.
Find the value of
\(p\);[2]
\(r\);[2]
\(q\).[2]
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\;\;\;\)\(\frac{{2 – 1}}{2},{\text{ }}2 – 1.5\)
\(p = 0.5\) A1 N2
[2 marks]
valid approach (M1)
eg\(\;\;\;\)\(\frac{{1 + 2}}{2}\)
\(r = 1.5\) A1 N2
[2 marks]
METHOD 1
valid approach (seen anywhere) M1
eg\(\;\;\;\)\(q = \frac{{2\pi }}{{{\text{period}}}},{\text{ }}\frac{{2\pi }}{{\left( {\frac{{2\pi }}{3}} \right)}}\)
period \( = \frac{{2\pi }}{3}\)\(\;\;\;\)(seen anywhere) (A1)
\(q = 3\) A1 N2
METHOD 2
attempt to substitute one point and their values for \(p\) and \(r\) into \(y\) M1
eg\(\;\;\;\)\(2 = 0.5\sin \left( {q\frac{\pi }{6}} \right) + 1.5,{\text{ }}\frac{\pi }{2} = 0.5\sin (q1) + 1.5\)
correct equation in \(q\) (A1)
eg\(\;\;\;\)\(q\frac{\pi }{6} = \frac{\pi }{2},{\text{ }}q\frac{\pi }{2} = \frac{{3\pi }}{2}\)
\(q = 3\) A1 N2
METHOD 3
valid reasoning comparing the graph with that of \(\sin x\) R1
eg\(\;\;\;\)position of max/min, graph goes faster
correct working (A1)
eg\(\;\;\;\)max at \(\frac{\pi }{6}\) not at \(\frac{\pi }{2}\), graph goes \(3\) times as fast
\(q = 3\) A1 N2
[3 marks]
Total [7 marks]
Question
The following diagram shows the graph of \(f(x) = a\sin bx + c\), for \(0 \leqslant x \leqslant 12\).
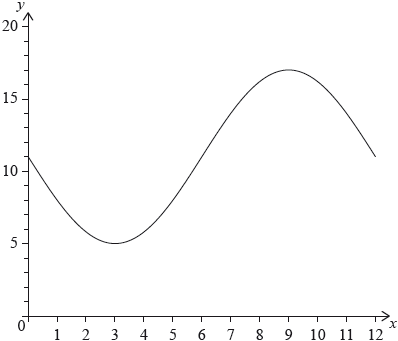
The graph of \(f\) has a minimum point at \((3,{\text{ }}5)\) and a maximum point at \((9,{\text{ }}17)\).
The graph of \(g\) is obtained from the graph of \(f\) by a translation of \(\left( {\begin{array}{*{20}{c}} k \\ 0 \end{array}} \right)\). The maximum point on the graph of \(g\) has coordinates \((11.5,{\text{ }}17)\).
The graph of \(g\) changes from concave-up to concave-down when \(x = w\).
(i) Find the value of \(c\).
(ii) Show that \(b = \frac{\pi }{6}\).
(iii) Find the value of \(a\).
(i) Write down the value of \(k\).
(ii) Find \(g(x)\).
(i) Find \(w\).
(ii) Hence or otherwise, find the maximum positive rate of change of \(g\).
Answer/Explanation
Markscheme
(i) valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{5 + 17}}{2}\)
\(c = 11\) A1 N2
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)period is 12, per \( = \frac{{2\pi }}{b},{\text{ }}9 – 3\)
\(b = \frac{{2\pi }}{{12}}\) A1
\(b = \frac{\pi }{6}\) AG N0
(iii) METHOD 1
valid approach (M1)
eg\(\,\,\,\,\,\)\(5 = a\sin \left( {\frac{\pi }{6} \times 3} \right) + 11\), substitution of points
\(a = – 6\) A1 N2
METHOD 2
valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{17 – 5}}{2}\), amplitude is 6
\(a = – 6\) A1 N2
[6 marks]
(i) \(k = 2.5\) A1 N1
(ii) \(g(x) = – 6\sin \left( {\frac{\pi }{6}(x – 2.5)} \right) + 11\) A2 N2
[3 marks]
(i) METHOD 1 Using \(g\)
recognizing that a point of inflexion is required M1
eg\(\,\,\,\,\,\)sketch, recognizing change in concavity
evidence of valid approach (M1)
eg\(\,\,\,\,\,\)\(g”(x) = 0\), sketch, coordinates of max/min on \({g’}\)
\(w = 8.5\) (exact) A1 N2
METHOD 2 Using \(f\)
recognizing that a point of inflexion is required M1
eg\(\,\,\,\,\,\)sketch, recognizing change in concavity
evidence of valid approach involving translation (M1)
eg\(\,\,\,\,\,\)\(x = w – k\), sketch, \(6 + 2.5\)
\(w = 8.5\) (exact) A1 N2
(ii) valid approach involving the derivative of \(g\) or \(f\) (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(g'(w),{\text{ }} – \pi \cos \left( {\frac{\pi }{6}x} \right)\), max on derivative, sketch of derivative
attempt to find max value on derivative M1
eg\(\,\,\,\,\,\)\( – \pi \cos \left( {\frac{\pi }{6}(8.5 – 2.5)} \right),{\text{ }}f'(6)\), dot on max of sketch
3.14159
max rate of change \( = \pi \) (exact), 3.14 A1 N2
[6 marks]
Question
At Grande Anse Beach the height of the water in metres is modelled by the function \(h(t) = p\cos (q \times t) + r\), where \(t\) is the number of hours after 21:00 hours on 10 December 2017. The following diagram shows the graph of \(h\) , for \(0 \leqslant t \leqslant 72\).
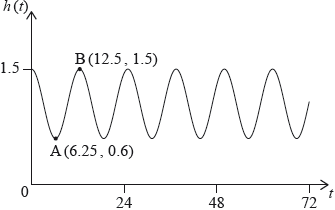
The point \({\text{A}}(6.25,{\text{ }}0.6)\) represents the first low tide and \({\text{B}}(12.5,{\text{ }}1.5)\) represents the next high tide.
How much time is there between the first low tide and the next high tide?
Find the difference in height between low tide and high tide.
Find the value of \(p\);
Find the value of \(q\);
Find the value of \(r\).
There are two high tides on 12 December 2017. At what time does the second high tide occur?
Answer/Explanation
Markscheme
attempt to find the difference of \(x\)-values of A and B (M1)
eg\(\,\,\,\,\,\)\(6.25 – 12.5{\text{ }}\)
6.25 (hours), (6 hours 15 minutes) A1 N2
[2 marks]
attempt to find the difference of \(y\)-values of A and B (M1)
eg\(\,\,\,\,\,\)\(1.5 – 0.6\)
\(0.9{\text{ (m)}}\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{{\text{max}} – {\text{min}}}}{2},{\text{ }}0.9 \div 2\)
\(p = 0.45\) A1 N2
[2 marks]
METHOD 1
period \( = 12.5\) (seen anywhere) (A1)
valid approach (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\({\text{period}} = \frac{{2\pi }}{b},{\text{ }}q = \frac{{2\pi }}{{{\text{period}}}},{\text{ }}\frac{{2\pi }}{{12.5}}\)
0.502654
\(q = \frac{{4\pi }}{{25}},{\text{ 0.503 }}\left( {{\text{or }} – \frac{{4\pi }}{{25}},{\text{ }} – 0.503} \right)\) A1 N2
METHOD 2
attempt to use a coordinate to make an equation (M1)
eg\(\,\,\,\,\,\)\(p\cos (6.25q) + r = 0.6,{\text{ }}p\cos (12.5q) + r = 1.5\)
correct substitution (A1)
eg\(\,\,\,\,\,\)\(0.45\cos (6.25q) + 1.05 = 0.6,{\text{ }}0.45\cos (12.5q) + 1.05 = 1.5\)
0.502654
\(q = \frac{{4\pi }}{{25}},{\text{ }}0.503{\text{ }}\left( {{\text{or }} – \frac{{4\pi }}{{25}},{\text{ }} – 0.503} \right)\) A1 N2
[3 marks]
valid method to find \(r\) (M1)
eg\(\,\,\,\,\,\)\(\frac{{{\text{max}} + {\text{min}}}}{2},{\text{ }}0.6 + 0.45\)
\(r = 1.05\) A1 N2
[2 marks]
METHOD 1
attempt to find start or end \(t\)-values for 12 December (M1)
eg\(\,\,\,\,\,\)\(3 + 24,{\text{ }}t = 27,{\text{ }}t = 51\)
finds \(t\)-value for second max (A1)
\(t = 50\)
23:00 (or 11 pm) A1 N3
METHOD 2
valid approach to list either the times of high tides after 21:00 or the \(t\)-values of high tides after 21:00, showing at least two times (M1)
eg\(\,\,\,\,\,\)\({\text{21:00}} + 12.5,{\text{ 21:00}} + 25,{\text{ }}12.5 + 12.5,{\text{ }}25 + 12.5\)
correct time of first high tide on 12 December (A1)
eg\(\,\,\,\,\,\)10:30 (or 10:30 am)
time of second high tide = 23:00 A1 N3
METHOD 3
attempt to set their \(h\) equal to 1.5 (M1)
eg\(\,\,\,\,\,\)\(h(t) = 1.5,{\text{ }}0.45\cos \left( {\frac{{4\pi }}{{25}}t} \right) + 1.05 = 1.5\)
correct working to find second max (A1)
eg\(\,\,\,\,\,\)\(0.503t = 8\pi ,{\text{ }}t = 50\)
23:00 (or 11 pm) A1 N3
[3 marks]
Question
Note: In this question, distance is in millimetres.
Let \(f(x) = x + a\sin \left( {x – \frac{\pi }{2}} \right) + a\), for \(x \geqslant 0\).
The graph of \(f\) passes through the origin. Let \({{\text{P}}_k}\) be any point on the graph of \(f\) with \(x\)-coordinate \(2k\pi \), where \(k \in \mathbb{N}\). A straight line \(L\) passes through all the points \({{\text{P}}_k}\).
Diagram 1 shows a saw. The length of the toothed edge is the distance AB.
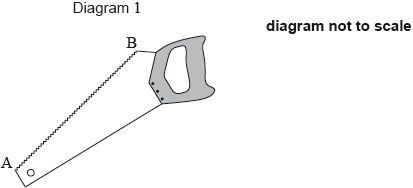
The toothed edge of the saw can be modelled using the graph of \(f\) and the line \(L\). Diagram 2 represents this model.
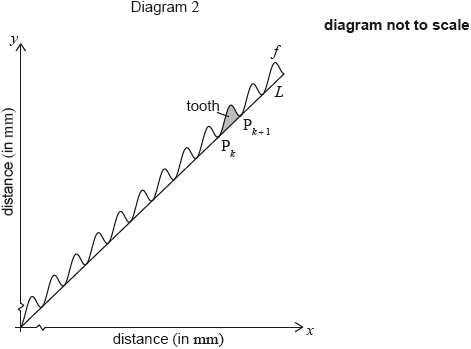
The shaded part on the graph is called a tooth. A tooth is represented by the region enclosed by the graph of \(f\) and the line \(L\), between \({{\text{P}}_k}\) and \({{\text{P}}_{k + 1}}\).
Show that \(f(2\pi ) = 2\pi \).
Find the coordinates of \({{\text{P}}_0}\) and of \({{\text{P}}_1}\).
Find the equation of \(L\).
Show that the distance between the \(x\)-coordinates of \({{\text{P}}_k}\) and \({{\text{P}}_{k + 1}}\) is \(2\pi \).
A saw has a toothed edge which is 300 mm long. Find the number of complete teeth on this saw.
Answer/Explanation
Markscheme
substituting \(x = 2\pi \) M1
eg\(\,\,\,\,\,\)\(2\pi + a\sin \left( {2\pi – \frac{\pi }{2}} \right) + a\)
\(2\pi + a\sin \left( {\frac{{3\pi }}{2}} \right) + a\) (A1)
\(2\pi – a + a\) A1
\(f(2\pi ) = 2\pi \) AG N0
[3 marks]
substituting the value of \(k\) (M1)
\({{\text{P}}_0}(0,{\text{ }}0),{\text{ }}{{\text{P}}_1}(2\pi ,{\text{ }}2\pi )\) A1A1 N3
[3 marks]
attempt to find the gradient (M1)
eg\(\,\,\,\,\,\)\(\frac{{2\pi – 0}}{{2\pi – 0}},{\text{ }}m = 1\)
correct working (A1)
eg\(\,\,\,\,\,\)\(\frac{{y – 2\pi }}{{x – 2\pi }} = 1,{\text{ }}b = 0,{\text{ }}y – 0 = 1(x – 0)\)
y = x A1 N3
[3 marks]
subtracting \(x\)-coordinates of \({{\text{P}}_{k + 1}}\) and \({{\text{P}}_k}\) (in any order) (M1)
eg\(\,\,\,\,\,\)\(2(k + 1)\pi – 2k\pi ,{\text{ }}2k\pi – 2k\pi – 2\pi \)
correct working (must be in correct order) A1
eg\(\,\,\,\,\,\)\(2k\pi + 2\pi – 2k\pi ,{\text{ }}\left| {2k\pi – 2(k + 1)\pi } \right|\)
distance is \(2\pi \) AG N0
[2 marks]
METHOD 1
recognizing the toothed-edge as the hypotenuse (M1)
eg\(\,\,\,\,\,\)\({300^2} = {x^2} + {y^2}\), sketch
correct working (using their equation of \(L\) (A1)
eg\(\,\,\,\,\,\)\({300^2} = {x^2} + {x^2}\)
\(x = \frac{{300}}{{\sqrt 2 }}\) (exact), 212.132 (A1)
dividing their value of \(x\) by \(2\pi {\text{ }}\left( {{\text{do not accept }}\frac{{300}}{{2\pi }}} \right)\) (M1)
eg\(\,\,\,\,\,\)\(\frac{{212.132}}{{2\pi }}\)
33.7618 (A1)
33 (teeth) A1 N2
METHOD 2
vertical distance of a tooth is \(2\pi \) (may be seen anywhere) (A1)
attempt to find the hypotenuse for one tooth (M1)
eg\(\,\,\,\,\,\)\({x^2} = {(2\pi )^2} + {(2\pi )^2}\)
\(x = \sqrt {8{\pi ^2}} \) (exact), 8.88576 (A1)
dividing 300 by their value of \(x\) (M1)
eg
33.7618 (A1)
33 (teeth) A1 N2
[6 marks]
Question
Let \(f\left( x \right) = 12\,\,{\text{cos}}\,x – 5\,\,{\text{sin}}\,x,\,\, – \pi \leqslant x \leqslant 2\pi \), be a periodic function with \(f\left( x \right) = f\left( {x + 2\pi } \right)\)
The following diagram shows the graph of \(f\).
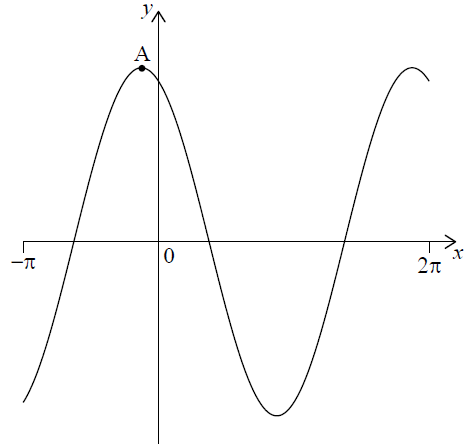
There is a maximum point at A. The minimum value of \(f\) is −13 .
A ball on a spring is attached to a fixed point O. The ball is then pulled down and released, so that it moves back and forth vertically.
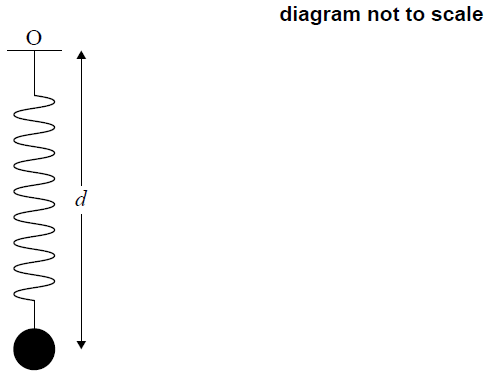
The distance, d centimetres, of the centre of the ball from O at time t seconds, is given by
\(d\left( t \right) = f\left( t \right) + 17,\,\,0 \leqslant t \leqslant 5.\)
Find the coordinates of A.
For the graph of \(f\), write down the amplitude.
For the graph of \(f\), write down the period.
Hence, write \(f\left( x \right)\) in the form \(p\,\,{\text{cos}}\,\left( {x + r} \right)\).
Find the maximum speed of the ball.
Find the first time when the ball’s speed is changing at a rate of 2 cm s−2.
Answer/Explanation
Markscheme
−0.394791,13
A(−0.395, 13) A1A1 N2
[2 marks]
13 A1 N1
[1 mark]
\({2\pi }\), 6.28 A1 N1
[1 mark]
valid approach (M1)
eg recognizing that amplitude is p or shift is r
\(f\left( x \right) = 13\,\,{\text{cos}}\,\left( {x + 0.395} \right)\) (accept p = 13, r = 0.395) A1A1 N3
Note: Accept any value of r of the form \(0.395 + 2\pi k,\,\,k \in \mathbb{Z}\)
[3 marks]
recognizing need for d ′(t) (M1)
eg −12 sin(t) − 5 cos(t)
correct approach (accept any variable for t) (A1)
eg −13 sin(t + 0.395), sketch of d′, (1.18, −13), t = 4.32
maximum speed = 13 (cms−1) A1 N2
[3 marks]
recognizing that acceleration is needed (M1)
eg a(t), d ”(t)
correct equation (accept any variable for t) (A1)
eg \(a\left( t \right) = – 2,\,\,\left| {\frac{{\text{d}}}{{{\text{d}}t}}\left( {d’\left( t \right)} \right)} \right| = 2,\,\, – 12\,\,{\text{cos}}\,\left( t \right) + 5\,\,{\text{sin}}\,\left( t \right) = – 2\)
valid attempt to solve their equation (M1)
eg sketch, 1.33
1.02154
1.02 A2 N3
[5 marks]
Question
At an amusement park, a Ferris wheel with diameter 111 metres rotates at a constant speed. The bottom of the wheel is k metres above the ground. A seat starts at the bottom of the wheel.
The wheel completes one revolution in 16 minutes.
After t minutes, the height of the seat above ground is given by \(h\left( t \right) = 61.5 + a\,{\text{cos}}\left( {\frac{\pi }{8}t} \right)\), for 0 ≤ t ≤ 32.
After 8 minutes, the seat is 117 m above the ground. Find k.
Find the value of a.
Find when the seat is 30 m above the ground for the third time.
Answer/Explanation
Markscheme
valid approach to find k (M1)
eg 8 minutes is half a turn, k + diameter, k + 111 = 117
k = 6 A1 N2
[2 marks]
METHOD 1
valid approach (M1)
eg \(\frac{{{\text{max}}\,\, – \,\,{\text{min}}}}{2}\) a = radius
\(\left| a \right| = \frac{{117 – 6}}{2},\,\,55.5\) (A1)
a = −55.5 A1 N2
METHOD 2
attempt to substitute valid point into equation for f (M1)
eg h(0) = 6, h(8) = 117
correct equation (A1)
eg \(6 = 61.5 + a\,{\text{cos}}\left( {\frac{\pi }{8} \times 0} \right),\,\,117 = 61.5 + a\,{\text{cos}}\left( {\frac{\pi }{8} \times 8} \right),\,\,6 = 61.5 + a\)
a = −55.5 A1 N2
[3 marks]
valid approach (M1)
eg sketch of h and \(y = 30,\,\,h = 30,\,\,61.5 – 55.5\,{\text{cos}}\left( {\frac{\pi }{8}t} \right) = 30,\,\,t = 2.46307,\,\,t = 13.5369\)
18.4630
t = 18.5 (minutes) A1 N3
[3 marks]

