Question
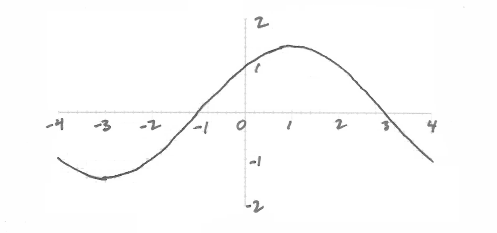
Let \(f(x) = \cos \left( {\frac{\pi }{4}x} \right) + \sin \left( {\frac{\pi }{4}x} \right),{\text{ for }} – 4 \leqslant x \leqslant 4.\)
Sketch the graph of \(f\).
Find the values of \(x\) where the function is decreasing.
The function \(f\) can also be written in the form \(f(x) = a\sin \left( {\frac{\pi }{4}(x + c)} \right)\), where \(a \in \mathbb{R}\), and \(0 \leqslant c \leqslant 2\). Find the value of \(a\);
The function \(f\) can also be written in the form \(f(x) = a\sin \left( {\frac{\pi }{4}(x + c)} \right)\), where \(a \in \mathbb{R}\), and \(0 \leqslant c \leqslant 2\). Find the value of \(c\).
Answer/Explanation
Markscheme
 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for approximately correct sinusoidal shape.
Only if this A1 is awarded, award the following:
A1 for correct domain,
A1 for approximately correct range.
[3 marks]
recognizes decreasing to the left of minimum or right of maximum,
eg \(f'(x) < 0\) (R1)
x-values of minimum and maximum (may be seen on sketch in part (a)) (A1)(A1)
eg \(x = – 3,{\text{ (1, 1.4)}}\)
two correct intervals A1A1 N5
eg \( – 4 < x < – 3,{\text{ }}1 \leqslant x \leqslant 4;{\text{ }}x < – 3,{\text{ }}x \geqslant 1\)
[5 marks]
recognizes that \(a\) is found from amplitude of wave (R1)
y-value of minimum or maximum (A1)
eg (−3, −1.41) , (1, 1.41)
\(a = 1.41421\)
\(a = \sqrt 2 {\text{, (exact), 1.41,}}\) A1 N3
[3 marks]
METHOD 1
recognize that shift for sine is found at x-intercept (R1)
attempt to find x-intercept (M1)
eg \(\cos \left( {\frac{\pi }{4}x} \right) + \sin \left( {\frac{\pi }{4}x} \right) = 0,{\text{ }}x = 3 + 4k,{\text{ }}k \in \mathbb{Z}\)
\(x = – 1\) (A1)
\(c = 1\) A1 N4
METHOD 2
attempt to use a coordinate to make an equation (R1)
eg \(\sqrt 2 \sin \left( {\frac{\pi }{4}c} \right) = 1,{\text{ }}\sqrt 2 \sin \left( {\frac{\pi }{4}(3 – c)} \right) = 0\)
attempt to solve resulting equation (M1)
eg sketch, \(x = 3 + 4k,{\text{ }}k \in \mathbb{Z}\)
\(x = – 1\) (A1)
\(c = 1\) A1 N4
[4 marks]
Question
The following diagram shows part of the graph of \(y = p\sin (qx) + r\).
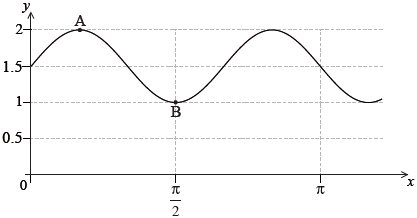
The point \({\text{A}}\left( {\frac{\pi }{6},{\text{ }}2} \right)\) is a maximum point and the point \({\text{B}}\left( {\frac{\pi }{6},{\text{ }}1} \right)\) is a minimum point.
Find the value of
\(p\);[2]
\(r\);[2]
\(q\).[2]
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\;\;\;\)\(\frac{{2 – 1}}{2},{\text{ }}2 – 1.5\)
\(p = 0.5\) A1 N2
[2 marks]
valid approach (M1)
eg\(\;\;\;\)\(\frac{{1 + 2}}{2}\)
\(r = 1.5\) A1 N2
[2 marks]
METHOD 1
valid approach (seen anywhere) M1
eg\(\;\;\;\)\(q = \frac{{2\pi }}{{{\text{period}}}},{\text{ }}\frac{{2\pi }}{{\left( {\frac{{2\pi }}{3}} \right)}}\)
period \( = \frac{{2\pi }}{3}\)\(\;\;\;\)(seen anywhere) (A1)
\(q = 3\) A1 N2
METHOD 2
attempt to substitute one point and their values for \(p\) and \(r\) into \(y\) M1
eg\(\;\;\;\)\(2 = 0.5\sin \left( {q\frac{\pi }{6}} \right) + 1.5,{\text{ }}\frac{\pi }{2} = 0.5\sin (q1) + 1.5\)
correct equation in \(q\) (A1)
eg\(\;\;\;\)\(q\frac{\pi }{6} = \frac{\pi }{2},{\text{ }}q\frac{\pi }{2} = \frac{{3\pi }}{2}\)
\(q = 3\) A1 N2
METHOD 3
valid reasoning comparing the graph with that of \(\sin x\) R1
eg\(\;\;\;\)position of max/min, graph goes faster
correct working (A1)
eg\(\;\;\;\)max at \(\frac{\pi }{6}\) not at \(\frac{\pi }{2}\), graph goes \(3\) times as fast
\(q = 3\) A1 N2
[3 marks]
Total [7 marks]
Question
The following diagram shows the graph of \(f(x) = a\sin bx + c\), for \(0 \leqslant x \leqslant 12\).
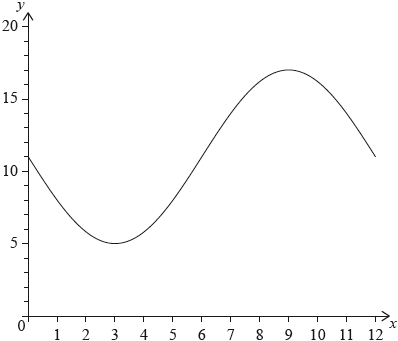
The graph of \(f\) has a minimum point at \((3,{\text{ }}5)\) and a maximum point at \((9,{\text{ }}17)\).
The graph of \(g\) is obtained from the graph of \(f\) by a translation of \(\left( {\begin{array}{*{20}{c}} k \\ 0 \end{array}} \right)\). The maximum point on the graph of \(g\) has coordinates \((11.5,{\text{ }}17)\).
The graph of \(g\) changes from concave-up to concave-down when \(x = w\).
(i) Find the value of \(c\).
(ii) Show that \(b = \frac{\pi }{6}\).
(iii) Find the value of \(a\).
(i) Write down the value of \(k\).
(ii) Find \(g(x)\).
(i) Find \(w\).
(ii) Hence or otherwise, find the maximum positive rate of change of \(g\).
Answer/Explanation
Markscheme
(i) valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{5 + 17}}{2}\)
\(c = 11\) A1 N2
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)period is 12, per \( = \frac{{2\pi }}{b},{\text{ }}9 – 3\)
\(b = \frac{{2\pi }}{{12}}\) A1
\(b = \frac{\pi }{6}\) AG N0
(iii) METHOD 1
valid approach (M1)
eg\(\,\,\,\,\,\)\(5 = a\sin \left( {\frac{\pi }{6} \times 3} \right) + 11\), substitution of points
\(a = – 6\) A1 N2
METHOD 2
valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{17 – 5}}{2}\), amplitude is 6
\(a = – 6\) A1 N2
[6 marks]
(i) \(k = 2.5\) A1 N1
(ii) \(g(x) = – 6\sin \left( {\frac{\pi }{6}(x – 2.5)} \right) + 11\) A2 N2
[3 marks]
(i) METHOD 1 Using \(g\)
recognizing that a point of inflexion is required M1
eg\(\,\,\,\,\,\)sketch, recognizing change in concavity
evidence of valid approach (M1)
eg\(\,\,\,\,\,\)\(g”(x) = 0\), sketch, coordinates of max/min on \({g’}\)
\(w = 8.5\) (exact) A1 N2
METHOD 2 Using \(f\)
recognizing that a point of inflexion is required M1
eg\(\,\,\,\,\,\)sketch, recognizing change in concavity
evidence of valid approach involving translation (M1)
eg\(\,\,\,\,\,\)\(x = w – k\), sketch, \(6 + 2.5\)
\(w = 8.5\) (exact) A1 N2
(ii) valid approach involving the derivative of \(g\) or \(f\) (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(g'(w),{\text{ }} – \pi \cos \left( {\frac{\pi }{6}x} \right)\), max on derivative, sketch of derivative
attempt to find max value on derivative M1
eg\(\,\,\,\,\,\)\( – \pi \cos \left( {\frac{\pi }{6}(8.5 – 2.5)} \right),{\text{ }}f'(6)\), dot on max of sketch
3.14159
max rate of change \( = \pi \) (exact), 3.14 A1 N2
[6 marks]
Question
The depth of water in a port is modelled by the function \(d(t) = p\cos qt + 7.5\), for \(0 \leqslant t \leqslant 12\), where \(t\) is the number of hours after high tide.
At high tide, the depth is 9.7 metres.
At low tide, which is 7 hours later, the depth is 5.3 metres.
Find the value of \(p\).
Find the value of \(q\).
Use the model to find the depth of the water 10 hours after high tide.
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{{\text{max}} – {\text{min}}}}{2}\), sketch of graph, \(9.7 = p\cos (0) + 7.5\)
\(p = 2.2\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(B = \frac{{2\pi }}{{{\text{period}}}}\), period is \(14,{\text{ }}\frac{{360}}{{14}},{\text{ }}5.3 = 2.2\cos 7q + 7.5\)
0.448798
\(q = \frac{{2\pi }}{{14}}{\text{ }}\left( {\frac{\pi }{7}} \right)\), (do not accept degrees) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(d(10),{\text{ }}2.2\cos \left( {\frac{{20\pi }}{{14}}} \right) + 7.5\)
7.01045
7.01 (m) A1 N2
[2 marks]
Question
Let \(f\left( x \right) = 12\,\,{\text{cos}}\,x – 5\,\,{\text{sin}}\,x,\,\, – \pi \leqslant x \leqslant 2\pi \), be a periodic function with \(f\left( x \right) = f\left( {x + 2\pi } \right)\)
The following diagram shows the graph of \(f\).
There is a maximum point at A. The minimum value of \(f\) is −13 .
A ball on a spring is attached to a fixed point O. The ball is then pulled down and released, so that it moves back and forth vertically.
The distance, d centimetres, of the centre of the ball from O at time t seconds, is given by
\(d\left( t \right) = f\left( t \right) + 17,\,\,0 \leqslant t \leqslant 5.\)
Find the coordinates of A.
For the graph of \(f\), write down the amplitude.
For the graph of \(f\), write down the period.
Hence, write \(f\left( x \right)\) in the form \(p\,\,{\text{cos}}\,\left( {x + r} \right)\).
Find the maximum speed of the ball.
Find the first time when the ball’s speed is changing at a rate of 2 cm s−2.
Answer/Explanation
Markscheme
−0.394791,13
A(−0.395, 13) A1A1 N2
[2 marks]
13 A1 N1
[1 mark]
\({2\pi }\), 6.28 A1 N1
[1 mark]
valid approach (M1)
eg recognizing that amplitude is p or shift is r
\(f\left( x \right) = 13\,\,{\text{cos}}\,\left( {x + 0.395} \right)\) (accept p = 13, r = 0.395) A1A1 N3
Note: Accept any value of r of the form \(0.395 + 2\pi k,\,\,k \in \mathbb{Z}\)
[3 marks]
recognizing need for d ′(t) (M1)
eg −12 sin(t) − 5 cos(t)
correct approach (accept any variable for t) (A1)
eg −13 sin(t + 0.395), sketch of d′, (1.18, −13), t = 4.32
maximum speed = 13 (cms−1) A1 N2
[3 marks]
recognizing that acceleration is needed (M1)
eg a(t), d ”(t)
correct equation (accept any variable for t) (A1)
eg \(a\left( t \right) = – 2,\,\,\left| {\frac{{\text{d}}}{{{\text{d}}t}}\left( {d’\left( t \right)} \right)} \right| = 2,\,\, – 12\,\,{\text{cos}}\,\left( t \right) + 5\,\,{\text{sin}}\,\left( t \right) = – 2\)
valid attempt to solve their equation (M1)
eg sketch, 1.33
1.02154
1.02 A2 N3
[5 marks]

