Question
Farmer Bill owns a rectangular field, 10 m by 4 m. Bill attaches a rope to a wooden post at one corner of his field, and attaches the other end to his goat Gruff.
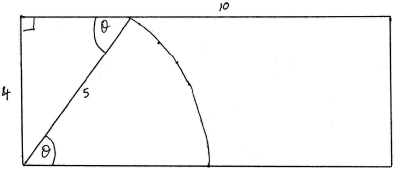
a.Given that the rope is 5 m long, calculate the percentage of Bill’s field that Gruff is able to graze. Give your answer correct to the nearest integer.[4]
b.Bill replaces Gruff’s rope with another, this time of length \(a,{\text{ }}4 < a < 10\), so that Gruff can now graze exactly one half of Bill’s field.
Show that \(a\) satisfies the equation
\[{a^2}\arcsin \left( {\frac{4}{a}} \right) + 4\sqrt {{a^2} – 16} = 40.\][4]
c.Find the value of \(a\).[2]
▶️Answer/Explanation
Markscheme
EITHER
area of triangle \( = \frac{1}{2} \times 3 \times 4\;\;\;( = 6)\) A1
area of sector \( = \frac{1}{2}\arcsin \left( {\frac{4}{5}} \right) \times {5^2}\;\;\;( = 11.5911 \ldots )\) A1
OR
\(\int_0^4 {\sqrt {25 – {x^2}} {\text{d}}x} \) M1A1
THEN
total area \( = 17.5911 \ldots {\text{ }}{{\text{m}}^2}\) (A1)
percentage \( = \frac{{17.5911 \ldots }}{{40}} \times 100 = 44\% \) A1
[4 marks]
METHOD 1
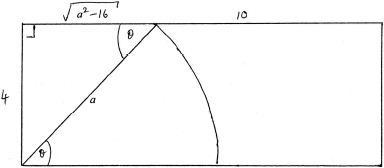
area of triangle \( = \frac{1}{2} \times 4 \times \sqrt {{a^2} – 16} \) A1
\(\theta = \arcsin \left( {\frac{4}{a}} \right)\) (A1)
area of sector \( = \frac{1}{2}{r^2}\theta = \frac{1}{2}{a^2}\arcsin \left( {\frac{4}{a}} \right)\) A1
therefore total area \( = 2\sqrt {{a^2} – 16} + \frac{1}{2}{a^2}\arcsin \left( {\frac{4}{a}} \right) = 20\) A1
rearrange to give: \({a^2}\arcsin \left( {\frac{4}{a}} \right) + 4\sqrt {{a^2} – 16} = 40\) AG
METHOD 2
\(\int_0^4 {\sqrt {{a^2} – {x^2}} {\text{d}}x = 20} \) M1
use substitution \(x = a\sin \theta ,{\text{ }}\frac{{{\text{d}}x}}{{{\text{d}}\theta }} = a\cos \theta \)
\(\int_0^{\arcsin \left( {\frac{4}{a}} \right)} {{a^2}{{\cos }^2}\theta {\text{d}}\theta = 20} \)
\(\frac{{{a^2}}}{2}\int_0^{\arcsin \left( {\frac{4}{a}} \right)} {(\cos 2\theta + 1){\text{d}}\theta = 20} \) M1
\({a^2}\left[ {\left( {\frac{{\sin 2\theta }}{2} + \theta } \right)} \right]_0^{\arcsin \left( {\frac{4}{a}} \right)} = 40\) A1
\({a^2}\left[ {(\sin \theta \cos \theta + \theta } \right]_0^{\arcsin \left( {\frac{4}{a}} \right)} = 40\)
\({a^2}\arcsin \left( {\frac{4}{a}} \right) + {a^2}\left( {\frac{4}{a}} \right)\sqrt {\left( {1 – {{\left( {\frac{4}{a}} \right)}^2}} \right)} = 40\) A1
\({a^2}\arcsin \left( {\frac{4}{a}} \right) + 4\sqrt {{a^2} – 16} = 40\) AG
[4 marks]
solving using \({\text{GDC}} \Rightarrow a = 5.53{\text{ cm}}\) A2
[2 marks]
Total [10 marks]
Question
Consider the function \(f\) defined by \(f(x) = 3x\arccos (x)\) where \( – 1 \leqslant x \leqslant 1\).
a.Sketch the graph of \(f\) indicating clearly any intercepts with the axes and the coordinates of any local maximum or minimum points.[3]
b.State the range of \(f\).[2]
c.Solve the inequality \(\left| {3x\arccos (x)} \right| > 1\).[4]
▶️Answer/Explanation
Markscheme
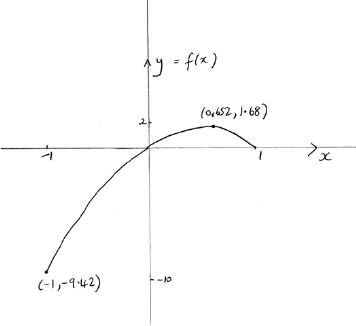
correct shape passing through the origin and correct domain A1
Note: Endpoint coordinates are not required. The domain can be indicated by \( – 1\) and 1 marked on the axis.
\((0.652,{\text{ }}1.68)\) A1
two correct intercepts (coordinates not required) A1
Note: A graph passing through the origin is sufficient for \((0,{\text{ }}0)\).
[3 marks]
\([-9.42,{\text{ }}1.68]{\text{ }}({\text{or }} – 3\pi ,{\text{ }}1.68])\) A1A1
Note: Award A1A0 for open or semi-open intervals with correct endpoints. Award A1A0 for closed intervals with one correct endpoint.
[2 marks]
attempting to solve either \(\left| {3x\arccos (x)} \right| > 1\) (or equivalent) or \(\left| {3x\arccos (x)} \right| = 1\) (or equivalent) (eg. graphically) (M1)
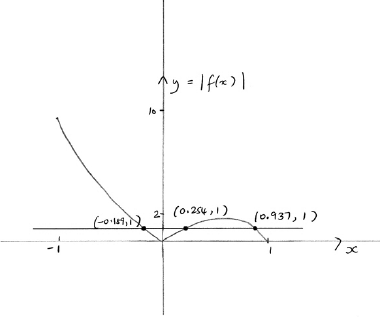
\(x = – 0.189,{\text{ }}0.254,{\text{ }}0.937\) (A1)
\( – 1 \leqslant x < – 0.189{\text{ or }}0.254 < x < 0.937\) A1A1
Note: Award A0 for \(x < – 0.189\).
[4 marks]
