Question
Points A, B and C are on the circumference of a circle, centre O and radius \(r\) . A trapezium OABC is formed such that AB is parallel to OC, and the angle \({\rm{A}}\hat {\text{O}}{\text{C}}\) is \(\theta\) , \(\frac{\pi }{2} \leqslant \theta \leqslant \pi \) .
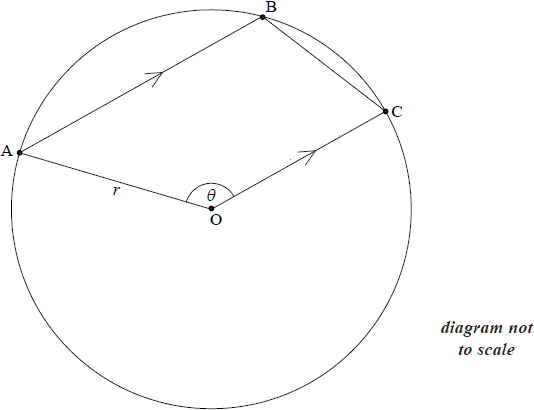
(a) Show that angle \({\rm{B\hat OC}}\) is \(\pi – \theta \).
(b) Show that the area, T, of the trapezium can be expressed as
\[T = \frac{1}{2}{r^2}\sin \theta – \frac{1}{2}{r^2}\sin 2\theta .\]
(c) (i) Show that when the area is maximum, the value of \(\theta \) satisfies
\[\cos \theta = 2\cos 2\theta .\]
(ii) Hence determine the maximum area of the trapezium when r = 1.
(Note: It is not required to prove that it is a maximum.)
▶️Answer/Explanation
Markscheme
(a) \({\rm{O\hat AB}} = \pi – \theta \,\,\,\,\,\)(allied) A1
recognizing OAB as an isosceles triangle M1
so \({\rm{A\hat BO}} = \pi – \theta \)
\({\rm{B\hat OC}} = \pi – \theta \,\,\,\,\,\)(alternate) AG
Note: This can be done in many ways, including a clear diagram.
[3 marks]
(b) area of trapezium is \(T = {\text{are}}{{\text{a}}_{\Delta {\text{BOC}}}} + {\text{are}}{{\text{a}}_{\Delta {\text{AOB}}}}\) (M1)
\( = \frac{1}{2}{r^2}\sin (\pi – \theta ) + \frac{1}{2}{r^2}\sin (2\theta – \pi )\) M1A1
\( = \frac{1}{2}{r^2}\sin \theta – \frac{1}{2}{r^2}\sin 2\theta \) AG
[3 marks]
(c) (i) \(\frac{{{\text{d}}T}}{{{\text{d}}\theta }} = \frac{1}{2}{r^2}\cos \theta – {r^2}\cos 2\theta \) M1A1
for maximum area \(\frac{1}{2}{r^2}\cos \theta – {r^2}\cos 2\theta = 0\) M1
\(\cos \theta = 2\cos 2\theta \) AG
(ii) \({\theta _{\max }} = 2.205 \ldots \) (A1)
\(\frac{1}{2}\sin {\theta _{\max }} – \frac{1}{2}\sin 2{\theta _{\max }} = 0.880\) A1
[5 marks]
Total [11 marks]
Examiners report
In part (a) students had difficulties supporting their statements and were consequently unable to gain all the marks here. There were some good attempts at parts (b) and (c) although many students failed to recognise r as a constant and hence differentiated it, often incorrectly.
Question
Triangle ABC has AB = 5 cm, BC = 6 cm and area 10 \({\text{c}}{{\text{m}}^2}\).
(a) Find \(\sin \hat B\).
(b) Hence, find the two possible values of AC, giving your answers correct to two decimal places.
▶️Answer/Explanation
Markscheme
(a) area \( = \frac{1}{2} \times {\text{BC}} \times {\text{AB}} \times \sin B\) (M1)
\(\left( {10 = \frac{1}{2} \times 5 \times 6 \times \sin B} \right)\)
\(\sin \hat B = \frac{2}{3}\) A1
(b) \(\cos B = \pm \frac{{\sqrt 5 }}{3}{\text{ }}( = \pm 0.7453 \ldots ){\text{ or }}B = 41.8 \ldots {\text{ and }}138.1 \ldots \) (A1)
\({\text{A}}{{\text{C}}^2} = {\text{B}}{{\text{C}}^2} + {\text{A}}{{\text{B}}^2} – 2 \times {\text{BC}} \times {\text{AB}} \times \cos B\) (M1)
\({\text{AC}} = \sqrt {{5^2} + {6^2} – 2 \times 5 \times 6 \times 0.7453 \ldots } {\text{ or }}\sqrt {{5^2} + {6^2} + 2 \times 5 \times 6 \times 0.7453 \ldots } \)
\({\text{AC}} = 4.03{\text{ or }}10.28\) A1A1
[6 marks]
Examiners report
Most candidates attempted this question and part (a) was answered correctly by most candidates but in (b), despite the wording of the question, the obtuse angle was often omitted leading to only one solution.
In many cases early rounding led to inaccuracy in the final answers and many candidates failed to round their answers to two decimal places as required.
Question
Consider the planes \({\pi _1}:x – 2y – 3z = 2{\text{ and }}{\pi _2}:2x – y – z = k\) .
Find the angle between the planes \({\pi _1}\)and \({\pi _2}\) .[4]
The planes \({\pi _1}\) and \({\pi _2}\) intersect in the line \({L_1}\) . Show that the vector equation of
\({L_1}\) is \(r = \left( {\begin{array}{*{20}{c}}
0\\
{2 – 3k}\\
{2k – 2}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right)\)[5]
The line \({L_2}\) has Cartesian equation \(5 – x = y + 3 = 2 – 2z\) . The lines \({L_1}\) and \({L_2}\) intersect at a point X. Find the coordinates of X.[5]
Determine a Cartesian equation of the plane \({\pi _3}\) containing both lines \({L_1}\) and \({L_2}\) .[5]
Let Y be a point on \({L_1}\) and Z be a point on \({L_2}\) such that XY is perpendicular to YZ and the area of the triangle XYZ is 3. Find the perimeter of the triangle XYZ.[5]
▶️Answer/Explanation
Markscheme
Note: Accept alternative notation for vectors (eg \(\langle a{\text{, }}b{\text{, }}c\rangle {\text{ or }}\left( {a{\text{, }}b{\text{, }}c} \right)\)).
\(\boldsymbol{n} = \left( {\begin{array}{*{20}{c}}
1 \\
{ – 2} \\
{ – 3}
\end{array}} \right)\) and \(\boldsymbol{m} = \left( {\begin{array}{*{20}{c}}
2 \\
{ – 1} \\
{ – 1}
\end{array}} \right)\) (A1)
\(\cos \theta = \frac{{\boldsymbol{n} \cdot \boldsymbol{m}}}{{\left| \boldsymbol{n} \right|\left| \boldsymbol{m} \right|}}\) (M1)
\(\cos \theta = \frac{{2 + 2 + 3}}{{\sqrt {1 + 4 + 9} \sqrt {4 + 1 + 1} }} = \frac{7}{{\sqrt {14} \sqrt 6 }}\) A1
\(\theta = 40.2^\circ \,\,\,\,\,(0.702{\text{ rad}})\) A1
[4 marks]
Note: Accept alternative notation for vectors (eg \(\langle a{\text{, }}b{\text{, }}c\rangle {\text{ or }}\left( {a{\text{, }}b{\text{, }}c} \right)\)).
METHOD 1
eliminate z from x – 2y – 3z = 2 and 2x – y – z = k
\(5x – y = 3k – 2 \Rightarrow x = \frac{{y – (2 – 3k)}}{5}\) M1A1
eliminate y from x – 2y – 3z = 2 and 2x – y – z = k
\(3x + z = 2k – 2 \Rightarrow x = \frac{{z – (2k – 2)}}{{ – 3}}\) A1
x = t, y = (2 − 3k) + 5t and z = (2k − 2) − 3t A1A1
\(r = \left( {\begin{array}{*{20}{c}}
0\\
{2 – 3k}\\
{2k – 2}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right)\) AG
[5 marks]
METHOD 2
\(\left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
{ – 3}
\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
{ – 1}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 1}\\
{ – 5}\\
3
\end{array}} \right) \Rightarrow {\text{direction is }}\left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right)\) M1A1
Let x = 0
\(0 – 2y – 3z = 2{\text{ and }}2 \times 0 – y – z = k\) (M1)
solve simultaneously (M1)
\(y = 2 – 3k{\text{ and }}z = 2k – 2\) A1
therefore r \( = \left( {\begin{array}{*{20}{c}}
0\\
{2 – 3k}\\
{2k – 2}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right)\) AG
[5 marks]
METHOD 3
substitute \(x = t,{\text{ }}y = (2 – 3k) + 5t{\text{ and }}z = (2k – 2) – 3t{\text{ into }}{\pi _1}{\text{ and }}{\pi _2}\) M1
for \({\pi _1}:t – 2(2 – 3k + 5t) – 3(2k – 2 – 3t) = 2\) A1
for \({\pi _2}:2t – (2 – 3k + 5t) – (2k – 2 – 3t) = k\) A1
the planes have a unique line of intersection R2
therefore the line is \(r = \left( {\begin{array}{*{20}{c}}
0\\
{2 – 3k}\\
{2k – 2}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right)\) AG
[5 marks]
Note: Accept alternative notation for vectors (eg \(\langle a{\text{, }}b{\text{, }}c\rangle {\text{ or }}\left( {a{\text{, }}b{\text{, }}c} \right)\)).
\(5 – t = (2 – 3k + 5t) + 3 = 2 – 2(2k – 2 – 3t)\) M1A1
Note: Award M1A1 if candidates use vector or parametric equations of \({L_2}\)
eg \(\left( {\begin{array}{*{20}{c}}
0\\
{2 – 3k}\\
{2k – 2}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
5\\
{ – 3}\\
1
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
{ – 2}\\
2\\
{ – 1}
\end{array}} \right)\) or \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{t = 5 – 2s}\\
{2 – 3k + 5t = – 3 + 2s}\\
{2k – 2 – 3t = 1 + s}
\end{array}} \right.\)
solve simultaneously M1
\(k = 2,{\text{ }}t = 1{\text{ }}(s = 2)\) A1
intersection point (\(1\), \(1\), \( – 1\)) A1
[5 marks]
Note: Accept alternative notation for vectors (eg \(\langle a{\text{, }}b{\text{, }}c\rangle {\text{ or }}\left( {a{\text{, }}b{\text{, }}c} \right)\)).
\({\overrightarrow l _2} = \left( {\begin{array}{*{20}{c}}
2\\
{ – 2}\\
1
\end{array}} \right)\) A1
\({\overrightarrow l _1} \times {\overrightarrow l _2} = \left| {\begin{array}{*{20}{c}}
\boldsymbol{i}&\boldsymbol{j}&\boldsymbol{k}\\
1&5&{ – 3}\\
2&{ – 2}&1
\end{array}} \right| = \left( {\begin{array}{*{20}{c}}
{ – 1}\\
{ – 7}\\
{ – 12}
\end{array}} \right)\) (M1)A1
\(\boldsymbol{r} \cdot \left( {\begin{array}{*{20}{c}}
1\\
7\\
{12}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1\\
1\\
{ – 1}
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
1\\
7\\
{12}
\end{array}} \right)\) (M1)
\(x + 7y + 12z = – 4\) A1
[5 marks]
Note: Accept alternative notation for vectors (eg \(\langle a{\text{, }}b{\text{, }}c\rangle {\text{ or }}\left( {a{\text{, }}b{\text{, }}c} \right)\)).
Let \(\theta \) be the angle between the lines \({\overrightarrow l _1} = \left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right)\) and \({\overrightarrow l _2} = \left( {\begin{array}{*{20}{c}}
2\\
{ – 2}\\
1
\end{array}} \right)\)
\(\cos \theta = \frac{{\left| {2 – 10 – 3} \right|}}{{\sqrt {35} \sqrt 9 }} \Rightarrow \theta = 0.902334…{\text{ }}51.699…^\circ )\) (M1)
as the triangle XYZ has a right angle at Y,
\({\text{XZ}} = a \Rightarrow {\text{YZ}} = a\sin \theta {\text{ and XY}} = a\cos \theta \) (M1)
\({\text{area = 3}} \Rightarrow \frac{{{a^2}\sin \theta \cos \theta }}{2} = 3\) (M1)
\(a = 3.5122…\) (A1)
perimeter \( = a + a\sin \theta + a\cos \theta = 8.44537… = 8.45\) A1
Note: If candidates attempt to find coordinates of Y and Z award M1 for expression of vector YZ in terms of two parameters, M1 for attempt to use perpendicular condition to determine relation between parameters, M1 for attempt to use the area to find the parameters and A2 for final answer.
[5 marks]
Examiners report
Although this was the last question in part B, it was answered surprisingly well by many candidates, except for part (e). Even those who had not done so well elsewhere often gained a number of marks in some parts of the question. Nevertheless the presence of parameters seemed to have blocked the abilities of weaker candidates to solve situations in which vectors were involved. Mathematical skills for this particular question were sometimes remarkable, however, calculations proved incomplete due to the way that planes were presented. Most candidates found a correct angle in part (a). Occasional arithmetic errors in calculating the magnitude of a vector and dot product occurred. In part (b) the vector product approach was popular. In some case candidates simply verified the result by substitution. There was a lot of simultaneous equation solving, much of which was not very pretty. In part (c), a number of candidates made errors when attempting to solve a system of equations involving parameters. Many of the results for the point were found in terms of k. It was notorious that candidates did not use their GDC to try to find the coordinates of the intersection point between lines. In part (d), a number of candidates used an incorrect point but this part was often done well.
Very few excellent answers to part (e) were seen using an efficient method. Most candidates attempted methods involving heavy algebraic manipulation and had little success in this part of the question.
Although this was the last question in part B, it was answered surprisingly well by many candidates, except for part (e). Even those who had not done so well elsewhere often gained a number of marks in some parts of the question. Nevertheless the presence of parameters seemed to have blocked the abilities of weaker candidates to solve situations in which vectors were involved. Mathematical skills for this particular question were sometimes remarkable, however, calculations proved incomplete due to the way that planes were presented. Most candidates found a correct angle in part (a). Occasional arithmetic errors in calculating the magnitude of a vector and dot product occurred. In part (b) the vector product approach was popular. In some case candidates simply verified the result by substitution. There was a lot of simultaneous equation solving, much of which was not very pretty. In part (c), a number of candidates made errors when attempting to solve a system of equations involving parameters. Many of the results for the point were found in terms of k. It was notorious that candidates did not use their GDC to try to find the coordinates of the intersection point between lines. In part (d), a number of candidates used an incorrect point but this part was often done well.
Very few excellent answers to part (e) were seen using an efficient method. Most candidates attempted methods involving heavy algebraic manipulation and had little success in this part of the question.
Although this was the last question in part B, it was answered surprisingly well by many candidates, except for part (e). Even those who had not done so well elsewhere often gained a number of marks in some parts of the question. Nevertheless the presence of parameters seemed to have blocked the abilities of weaker candidates to solve situations in which vectors were involved. Mathematical skills for this particular question were sometimes remarkable, however, calculations proved incomplete due to the way that planes were presented. Most candidates found a correct angle in part (a). Occasional arithmetic errors in calculating the magnitude of a vector and dot product occurred. In part (b) the vector product approach was popular. In some case candidates simply verified the result by substitution. There was a lot of simultaneous equation solving, much of which was not very pretty. In part (c), a number of candidates made errors when attempting to solve a system of equations involving parameters. Many of the results for the point were found in terms of k. It was notorious that candidates did not use their GDC to try to find the coordinates of the intersection point between lines. In part (d), a number of candidates used an incorrect point but this part was often done well.
Very few excellent answers to part (e) were seen using an efficient method. Most candidates attempted methods involving heavy algebraic manipulation and had little success in this part of the question.
Although this was the last question in part B, it was answered surprisingly well by many candidates, except for part (e). Even those who had not done so well elsewhere often gained a number of marks in some parts of the question. Nevertheless the presence of parameters seemed to have blocked the abilities of weaker candidates to solve situations in which vectors were involved. Mathematical skills for this particular question were sometimes remarkable, however, calculations proved incomplete due to the way that planes were presented. Most candidates found a correct angle in part (a). Occasional arithmetic errors in calculating the magnitude of a vector and dot product occurred. In part (b) the vector product approach was popular. In some case candidates simply verified the result by substitution. There was a lot of simultaneous equation solving, much of which was not very pretty. In part (c), a number of candidates made errors when attempting to solve a system of equations involving parameters. Many of the results for the point were found in terms of k. It was notorious that candidates did not use their GDC to try to find the coordinates of the intersection point between lines. In part (d), a number of candidates used an incorrect point but this part was often done well.
Very few excellent answers to part (e) were seen using an efficient method. Most candidates attempted methods involving heavy algebraic manipulation and had little success in this part of the question.
Although this was the last question in part B, it was answered surprisingly well by many candidates, except for part (e). Even those who had not done so well elsewhere often gained a number of marks in some parts of the question. Nevertheless the presence of parameters seemed to have blocked the abilities of weaker candidates to solve situations in which vectors were involved. Mathematical skills for this particular question were sometimes remarkable, however, calculations proved incomplete due to the way that planes were presented. Most candidates found a correct angle in part (a). Occasional arithmetic errors in calculating the magnitude of a vector and dot product occurred. In part (b) the vector product approach was popular. In some case candidates simply verified the result by substitution. There was a lot of simultaneous equation solving, much of which was not very pretty. In part (c), a number of candidates made errors when attempting to solve a system of equations involving parameters. Many of the results for the point were found in terms of k. It was notorious that candidates did not use their GDC to try to find the coordinates of the intersection point between lines. In part (d), a number of candidates used an incorrect point but this part was often done well.
Very few excellent answers to part (e) were seen using an efficient method. Most candidates attempted methods involving heavy algebraic manipulation and had little success in this part of the question.
Question
Compactness is a measure of how compact an enclosed region is.
The compactness, \(C\) , of an enclosed region can be defined by \(C = \frac{{4A}}{{\pi {d^2}}}\), where \(A\) is the area of the region and \(d\) is the maximum distance between any two points in the region.
For a circular region, \(C = 1\).
Consider a regular polygon of \(n\) sides constructed such that its vertices lie on the circumference of a circle of diameter \(x\) units.
If \(n > 2\) and even, show that \(C = \frac{n}{{2\pi }}\sin \frac{{2\pi }}{n}\).[3]
If \(n > 1\) and odd, it can be shown that \(C = \frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}}\).
Find the regular polygon with the least number of sides for which the compactness is more than \(0.99\).[4]
If \(n > 1\) and odd, it can be shown that \(C = \frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}}\).
Comment briefly on whether C is a good measure of compactness.[1]
▶️Answer/Explanation
Markscheme
each triangle has area \(\frac{1}{8}{x^2}\sin \frac{{2\pi }}{n}\;\;\;({\text{use of }}\frac{1}{2}ab\sin C)\) (M1)
there are \(n\) triangles so \(A = \frac{1}{8}n{x^2}\sin \frac{{2\pi }}{n}\) A1
\(C = \frac{{4\left( {\frac{1}{8}n{x^2}\sin \frac{{2\pi }}{n}} \right)}}{{\pi {n^2}}}\) A1
so \(C = \frac{n}{{2\pi }}\sin \frac{{2\pi }}{n}\) AG
[3 marks]
attempting to find the least value of \(n\) such that \(\frac{n}{{2\pi }}\sin \frac{{2\pi }}{n} > 0.99\) (M1)
\(n = 26\) A1
attempting to find the least value of \(n\) such that \(\frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}} > 0.99\) (M1)
\(n = 21\) (and so a regular polygon with 21 sides) A1
Note: Award (M0)A0(M1)A1 if \(\frac{n}{{2\pi }}\sin \frac{{2\pi }}{n} > 0.99\) is not considered and \(\frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}} > 0.99\) is correctly considered.
Award (M1)A1(M0)A0 for \(n = 26\).
[4 marks]
EITHER
for even and odd values of n, the value of C seems to increase towards the limiting value of the circle \((C = 1)\) ie as n increases, the polygonal regions get closer and closer to the enclosing circular region R1
OR
the differences between the odd and even values of n illustrate that this measure of compactness is not a good one. R1
Examiners report
Most candidates found this a difficult question with a large number of candidates either not attempting it or making little to no progress. In part (a), a number of candidates attempted to show the desired result using specific regular polygons. Some candidates attempted to fudge the result.
In part (b), the overwhelming majority of candidates that obtained either \(n = 21\) or \(n = 26\) or both used either a GDC numerical solve feature or a graphical approach rather than a tabular approach which is more appropriate for a discrete variable such as the number of sides of a regular polygon. Some candidates wasted valuable time by showing that \(C = \frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}}\) (a given result).
In part (c), the occasional candidate correctly commented that \(C \) was a good measure of compactness either because the value of \(C \) seemed to approach the limiting value of the circle as \(n \) increased or commented that \(C \) was not a good measure because of the disparity in \(C \)-values between even and odd values of \(n \).
Question
Barry is at the top of a cliff, standing 80 m above sea level, and observes two yachts in the sea.
“Seaview” \((S)\) is at an angle of depression of 25°.
“Nauti Buoy” \((N)\) is at an angle of depression of 35°.
The following three dimensional diagram shows Barry and the two yachts at S and N.
X lies at the foot of the cliff and angle \({\text{SXN}} = \) 70°.
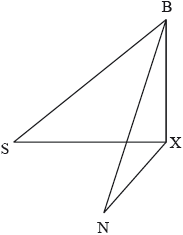
Find, to 3 significant figures, the distance between the two yachts.
▶️Answer/Explanation
Markscheme
attempt to use tan, or sine rule, in triangle BXN or BXS (M1)
\({\text{NX}} = 80\tan 55{\rm{^\circ }}\left( { = \frac{{80}}{{\tan 35{\rm{^\circ }}}} = 114.25} \right)\) (A1)
\({\text{SX}} = 80\tan 65{\rm{^\circ }}\left( { = \frac{{80}}{{\tan 25{\rm{^\circ }}}} = 171.56} \right)\) (A1)
Attempt to use cosine rule M1
\({\text{S}}{{\text{N}}^2} = {171.56^2} + {114.25^2} – 2 \times 171.56 \times 114.25\cos 70\)° (A1)
\({\text{SN}} = 171{\text{ }}({\text{m}})\) A1
Note: Award final A1 only if the correct answer has been given to 3 significant figures.
[6 marks]
Examiners report
Question
In a triangle \({\text{ABC, AB}} = 4{\text{ cm, BC}} = 3{\text{ cm}}\) and \({\rm{B\hat AC}} = \frac{\pi }{9}\).
Use the cosine rule to find the two possible values for AC.
Find the difference between the areas of the two possible triangles ABC.
▶️Answer/Explanation
Markscheme
METHOD 1
let \({\text{AC}} = x\)
\({3^2} = {x^2} + {4^2} – 8x\cos \frac{\pi }{9}\) M1A1
attempting to solve for \(x\) (M1)
\(x = 1.09,{\text{ }}6.43\) A1A1
METHOD 2
let \({\text{AC}} = x\)
using the sine rule to find a value of \(C\) M1
\({4^2} = {x^2} + {3^2} – 6x\cos (152.869 \ldots ^\circ ) \Rightarrow x = 1.09\) (M1)A1
\({4^2} = {x^2} + {3^2} – 6x\cos (27.131 \ldots ^\circ ) \Rightarrow x = 6.43\) (M1)A1
METHOD 3
let \({\text{AC}} = x\)
using the sine rule to find a value of \(B\) and a value of \(C\) M1
obtaining \(B = 132.869 \ldots ^\circ ,{\text{ }}7.131 \ldots ^\circ \) and \(C = 27.131 \ldots ^\circ ,{\text{ }}152.869 \ldots ^\circ \) A1
\((B = 2.319 \ldots ,{\text{ }}0.124 \ldots \) and \(C = 0.473 \ldots ,{\text{ }}2.668 \ldots )\)
attempting to find a value of \(x\) using the cosine rule (M1)
\(x = 1.09,{\text{ }}6.43\) A1A1
Note: Award M1A0(M1)A1A0 for one correct value of \(x\)
[5 marks]
\(\frac{1}{2} \times 4 \times 6.428 \ldots \times \sin \frac{\pi }{9}\) and \(\frac{1}{2} \times 4 \times 1.088 \ldots \times \sin \frac{\pi }{9}\) (A1)
(\(4.39747 \ldots \) and \(0.744833 \ldots \))
let \(D\) be the difference between the two areas
\(D = \frac{1}{2} \times 4 \times 6.428 \ldots \times \sin \frac{\pi }{9} – \frac{1}{2} \times 4 \times 1.088 \ldots \times \sin \frac{\pi }{9}\) (M1)
\((D = 4.39747 \ldots – 0.744833 \ldots )\)
\( = 3.65{\text{ (c}}{{\text{m}}^2})\) A1
[3 marks]
Examiners report
[N/A]
[N/A]
Question
ABCD is a quadrilateral where \({\text{AB}} = 6.5,{\text{ BC}} = 9.1,{\text{ CD}} = 10.4,{\text{ DA}} = 7.8\) and \({\rm{C\hat DA}} = 90^\circ \). Find \({\rm{A\hat BC}}\), giving your answer correct to the nearest degree.
▶️Answer/Explanation
Markscheme
\({\text{A}}{{\text{C}}^2} = {7.8^2} + {10.4^2}\) (M1)
\({\text{AC}} = 13\) (A1)
use of cosine rule eg, \(\cos ({\rm{A\hat BC}}) = \frac{{{{6.5}^2} + {{9.1}^2} – {{13}^2}}}{{2(6.5)(9.1)}}\) M1
\({\rm{A\hat BC}} = 111.804 \ldots ^\circ {\text{ }}( = 1.95134 \ldots )\) (A1)
\( = 112^\circ \) A1
[5 marks]
Examiners report
Well done by most candidates. A small number of candidates did not express the required angle correct to the nearest degree.
Question
Triangle \(ABC\) has area \({\text{21 c}}{{\text{m}}^{\text{2}}}\). The sides \(AB\) and \(AC\) have lengths \(6\) cm and \(11\) cm respectively. Find the two possible lengths of the side \(BC\).
▶️Answer/Explanation
Markscheme
\(21 = \frac{1}{2} \bullet 6 \bullet 11 \bullet \sin A\) (M1)
\(\sin A = \frac{7}{{11}}\) (A1)
EITHER
\(\hat A = 0.6897 \ldots ,{\text{ }}2.452 \ldots \left( {\hat A = \arcsin \frac{7}{{11}},{\text{ }}\pi – \arcsin \frac{7}{{11}} = 39.521 \ldots ^\circ ,{\text{ }}140.478 \ldots ^\circ } \right)\) (A1)
OR
\(\cos A = \pm \frac{{6\sqrt 2 }}{{11}}\;\;\;( = \pm 0.771 \ldots )\) (A1)
THEN
\({\text{B}}{{\text{C}}^2} = {6^2} + {11^2} – 2 \bullet 6 \bullet 11\cos A\) (M1)
\({\text{BC}} = 16.1\) or \(7.43\) A1A1
Note: Award M1A1A0M1A1A0 if only one correct solution is given.
[6 marks]
Examiners report
Question
A triangle \(ABC\) has \(\hat A = 50^\circ \), \({\text{AB}} = 7{\text{ cm}}\) and \({\text{BC}} = 6{\text{ cm}}\). Find the area of the triangle given that it is smaller than \(10{\text{ c}}{{\text{m}}^2}\).
▶️Answer/Explanation
Markscheme
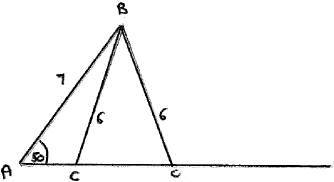
METHOD 1
\(\frac{6}{{\sin 50}} = \frac{7}{{\sin C}} \Rightarrow \sin C = \frac{{7\sin 50}}{6}\) (M1)
\(C = 63.344 \ldots \) (A1)
or\(\;\;\;C = 116.655 \ldots \) (A1)
\(B = 13.344 \ldots \;\;\;({\text{or }}B = 66.656 \ldots )\) (A1)
\({\text{area}} = \frac{1}{2} \times 6 \times 7 \times \sin 13.344 \ldots \;\;\;\left( {{\text{or }}\frac{1}{2} \times 6 \times 7 \times \sin 66.656 \ldots } \right)\) (M1)
\(4.846 \ldots \;\;\;({\text{or }} = 19.281 \ldots )\)
so answer is \(4.85{\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1
METHOD 2
\({6^2} = {7^2} + {b^2} – 2 \times 7b\cos 50\) (M1)(A1)
\({b^2} – 14b\cos 50 + 13 = 0\;\;\;\)or equivalent method to solve the above equation (M1)
\(b = 7.1912821 \ldots \;\;\;{\text{or}}\;\;\;b = 1.807744 \ldots \) (A1)
\({\text{area}} = \frac{1}{2} \times 7 \times 1.8077 \ldots \sin 50 = 4.846 \ldots \) (M1)
\(\left( {{\text{or }}\frac{1}{2} \times 7 \times 7.1912821 \ldots \sin 50 = 19.281 \ldots } \right)\)
so answer is \(4.85{\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1
METHOD 3
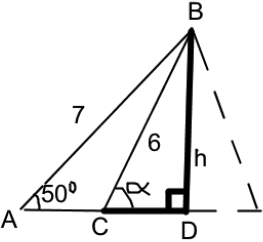
Diagram showing triangles \(ACB\) and \(ADB\) (M1)
\(h = 7\sin (50) = 5.3623 \ldots {\text{ (cm)}}\) (M1)
\(\alpha = \arcsin \frac{h}{6} = 63.3442 \ldots \) (M1)
\({\text{AC}} = {\text{AD}} – {\text{CD}} = 7\cos 50 – 6\cos \alpha = 1.8077 \ldots {\text{ (cm)}}\) (M1)
\({\text{area}} = \frac{1}{2} \times 1.8077 \ldots \times 5.3623 \ldots \) (M1)
\( = 4.85{\text{ (c}}{{\text{m}}^{\text{2}}}{\text{)}}\) A1
Total [6 marks]
Examiners report
Most candidates scored 4/6 showing that candidates do not have enough experience with the ambiguous case. Very few candidates drew a suitable diagram that would have illustrated this fact which could have helped them to understand the requirement that the answer should be less than 10. In fact many candidates ignored this requirement or used it incorrectly to solve an inequality.
