IB DP Maths Topic 4.1 Algebraic and geometric approaches to multiplication by a scalar, kv ; parallel vectors SL Paper 1

correct approach A1

eg \(\mathop {{\text{AO}}}\limits^ \to \,\, + \,\,\mathop {{\text{OB}}}\limits^ \to ,\,\,\,{\text{B}} – {\text{A}}\,{\text{, }}\,\left( \begin{gathered}
\,\,2 \hfill \\
– 4 \hfill \\
– 4 \hfill \\
\end{gathered} \right) – \left( \begin{gathered}
\, – 4 \hfill \\
– 12 \hfill \\
\,\,\,1 \hfill \\
\end{gathered} \right)\)

\(\mathop {{\text{AB}}}\limits^ \to = \left( \begin{gathered}
\,6 \hfill \\
\,8 \hfill \\
– 5 \hfill \\
\end{gathered} \right)\) AG N0

[1 mark]

any correct equation in the form r = a + tb (any parameter for t) A2 N2

where a is \(\left( \begin{gathered}
\,\,2 \hfill \\
– 4 \hfill \\
– 4 \hfill \\
\end{gathered} \right)\) or \(\left( \begin{gathered}
\, – 4 \hfill \\
– 12 \hfill \\
\,\,\,1 \hfill \\
\end{gathered} \right)\) and b is a scalar multiple of \(\left( \begin{gathered}
\,6 \hfill \\
\,8 \hfill \\
– 5 \hfill \\
\end{gathered} \right)\)

eg r \( = \left( \begin{gathered}
\, – 4 \hfill \\
– 12 \hfill \\
\,\,\,1 \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
\,6 \hfill \\
\,8 \hfill \\
– 5 \hfill \\
\end{gathered} \right),\,\,\left( {x,\,\,y,\,\,z} \right) = \left( {2,\,\, – 4,\,\, – 4} \right) + t\left( {6,\,\,8,\,\, – 5} \right),\) r \( = \left( \begin{gathered}
\, – 4 + 6t \hfill \\
– 12 + 8t \hfill \\
\,\,\,1 – 5t \hfill \\
\end{gathered} \right)\)

Note: Award A1 for the form a + tb, A1 for the form L = a + tb, A0 for the form r = b + ta.

[2 marks]

METHOD 1 (solving for t)

valid approach (M1)

eg \(\left( \begin{gathered}
\,k \hfill \\
12 \hfill \\
– k \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
\,\,2 \hfill \\
– 4 \hfill \\
– 4 \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
\,6 \hfill \\
\,8 \hfill \\
– 5 \hfill \\
\end{gathered} \right),\,\,\left( \begin{gathered}
\,k \hfill \\
12 \hfill \\
– k \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
\, – 4 \hfill \\
– 12 \hfill \\
\,\,\,1 \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
\,6 \hfill \\
\,8 \hfill \\
– 5 \hfill \\
\end{gathered} \right)\)

one correct equation A1

eg −4 + 8t = 12, −12 + 8t = 12

correct value for t (A1)

eg t = 2 or 3

correct substitution A1

eg 2 + 6(2), −4 + 6(3), −[1 + 3(−5)]

k = 14 AG N0

METHOD 2 (solving simultaneously)

valid approach (M1)

eg \(\left( \begin{gathered}
\,k \hfill \\
12 \hfill \\
– k \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
\,\,2 \hfill \\
– 4 \hfill \\
– 4 \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
\,6 \hfill \\
\,8 \hfill \\
– 5 \hfill \\
\end{gathered} \right),\,\,\left( \begin{gathered}
\,k \hfill \\
12 \hfill \\
– k \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
\, – 4 \hfill \\
– 12 \hfill \\
\,\,\,1 \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
\,6 \hfill \\
\,8 \hfill \\
– 5 \hfill \\
\end{gathered} \right)\)

two correct equations in A1

eg k = −4 + 6t, −k = 1 −5t

EITHER (eliminating k)

correct value for t (A1)

eg t = 2 or 3

correct substitution A1

eg 2 + 6(2), −4 + 6(3)

OR (eliminating t)

correct equation(s) (A1)

eg 5k + 20 = 30t and −6k − 6 = 30t, −k = 1 − 5\(\left( {\frac{{k + 4}}{6}} \right)\)

correct working clearly leading to k = 14 A1

eg −k + 14 = 0, −6k = 6 −5k − 20, 5k = −20 + 6(1 + k)

THEN

k = 14 AG N0

[4 marks]

correct substitution into scalar product A1

eg (2)(6) − (4)(8) − (4)(−5), 12 − 32 + 20

\(\mathop {{\text{OB}}}\limits^ \to \, \bullet \mathop {{\text{AB}}}\limits^ \to \) = 0 A1 N0

[2 marks]

\({\text{O}}\mathop {\text{B}}\limits^ \wedge {\text{A}} = \frac{\pi }{2},\,\,90^\circ \,\,\,\,\,\left( {{\text{accept}}\,\frac{{3\pi }}{2},\,\,270^\circ } \right)\,\) A1 N1

[1 marks]

METHOD 1 (\(\frac{1}{2}\) × height × CD)

recognizing that OB is altitude of triangle with base CD (seen anywhere) M1

eg \(\frac{1}{2} \times \left| {\mathop {{\text{OB}}}\limits^ \to } \right| \times \left| {\mathop {{\text{CD}}}\limits^ \to } \right|,\,\,{\text{OB}} \bot {\text{CD}},\) sketch showing right angle at B

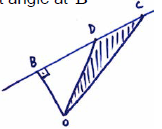
\(\mathop {{\text{CD}}}\limits^ \to = \left( \begin{gathered}
– 6 \hfill \\
– 8 \hfill \\
\,5 \hfill \\
\end{gathered} \right)\) or \(\mathop {{\text{DC}}}\limits^ \to = \left( \begin{gathered}
\,6 \hfill \\
\,8 \hfill \\
– 5 \hfill \\
\end{gathered} \right)\) (seen anywhere) (A1)

correct magnitudes (seen anywhere) (A1)(A1)

\(\left| {\mathop {{\text{OB}}}\limits^ \to } \right| = \sqrt {{{\left( 2 \right)}^2} + {{\left( { – 4} \right)}^2} + {{\left( { – 4} \right)}^2}} = \left( {\sqrt {36} } \right)\)

\(\left| {\mathop {{\text{CD}}}\limits^ \to } \right| = \sqrt {{{\left( { – 6} \right)}^2} + {{\left( { – 8} \right)}^2} + {{\left( 5 \right)}^2}} = \left( {\sqrt {125} } \right)\)

correct substitution into \(\frac{1}{2}bh\) A1

eg \(\frac{1}{2} \times 6 \times \sqrt {125} \)

area \( = 3\sqrt {125} ,\,\,15\sqrt 5 \) A1 N3

METHOD 2 (subtracting triangles)

recognizing that OB is altitude of either ΔOBD or ΔOBC(seen anywhere) M1

eg \(\frac{1}{2} \times \left| {\mathop {{\text{OB}}}\limits^ \to } \right| \times \left| {\mathop {{\text{BD}}}\limits^ \to } \right|,\,\,{\text{OB}} \bot {\text{BC}},\) sketch of triangle showing right angle at B

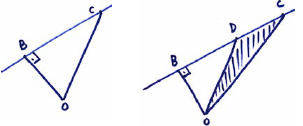
one correct vector \(\mathop {{\text{BD}}}\limits^ \to \) or \(\mathop {{\text{DB}}}\limits^ \to \) or \(\mathop {{\text{BC}}}\limits^ \to \) or \(\mathop {{\text{CB}}}\limits^ \to \) (seen anywhere) (A1)

eg \(\mathop {{\text{BD}}}\limits^ \to = \left( \begin{gathered}
\,6 \hfill \\
\,8 \hfill \\
– 5 \hfill \\
\end{gathered} \right)\), \(\mathop {{\text{CB}}}\limits^ \to = \left( \begin{gathered}
– 12 \hfill \\
– 16 \hfill \\
\,10 \hfill \\
\end{gathered} \right)\)

\(\left| {\mathop {{\text{OB}}}\limits^ \to } \right| = \sqrt {{{\left( 2 \right)}^2} + {{\left( { – 4} \right)}^2} + {{\left( { – 4} \right)}^2}} = \left( {\sqrt {36} } \right)\) (seen anywhere) (A1)

one correct magnitude of a base (seen anywhere) (A1)

\(\left| {\mathop {{\text{BD}}}\limits^ \to } \right| = \sqrt {{{\left( 6 \right)}^2} + {{\left( 8 \right)}^2} + {{\left( 5 \right)}^2}} = \left( {\sqrt {125} } \right),\,\,\left| {\mathop {{\text{BC}}}\limits^ \to } \right| = \sqrt {144 + 256 + 100} = \left( {\sqrt {500} } \right)\)

correct working A1

eg \(\frac{1}{2} \times 6 \times \sqrt {500} – \frac{1}{2} \times 6 \times 5\sqrt 5 ,\,\,\frac{1}{2} \times 6 \times \sqrt {500} \times {\text{sin}}90 – \frac{1}{2} \times 6 \times 5\sqrt 5 \times {\text{sin}}90\)

area \( = 3\sqrt {125} ,\,\,15\sqrt 5 \) A1 N3

METHOD 3 (using \(\frac{1}{2}\)ab sin C with ΔOCD)

two correct side lengths (seen anywhere) (A1)(A1)

\(\left| {\mathop {{\text{OD}}}\limits^ \to } \right| = \sqrt {{{\left( 8 \right)}^2} + {{\left( 4 \right)}^2} + {{\left( { – 9} \right)}^2}} = \left( {\sqrt {161} } \right),\,\,\left| {\mathop {{\text{CD}}}\limits^ \to } \right| = \sqrt {{{\left( { – 6} \right)}^2} + {{\left( { – 8} \right)}^2} + {{\left( 5 \right)}^2}} = \left( {\sqrt {125} } \right),\,\) \(\left| {\mathop {{\text{OC}}}\limits^ \to } \right| = \sqrt {{{\left( {14} \right)}^2} + {{\left( {12} \right)}^2} + {{\left( { – 14} \right)}^2}} = \left( {\sqrt {536} } \right)\)

attempt to find cosine ratio (seen anywhere) M1
eg \(\frac{{536 – 286}}{{ – 2\sqrt {161} \sqrt {125} }},\,\,\frac{{{\text{OD}} \bullet {\text{DC}}}}{{\left| {OD} \right|\left| {DC} \right|}}\)

correct working for sine ratio A1

eg \(\frac{{{{\left( {125} \right)}^2}}}{{161 \times 125}} + {\text{si}}{{\text{n}}^2}\,D = 1\)

correct substitution into \(\frac{1}{2}ab\,\,{\text{sin}}\,C\) A1

eg \(0.5 \times \sqrt {161} \times \sqrt {125} \times \frac{6}{{\sqrt {161} }}\)

area \( = 3\sqrt {125} ,\,\,15\sqrt 5 \) A1 N3

[6 marks]