Question
The following diagram shows the cuboid (rectangular solid) OABCDEFG, where O is the origin, and \(\overrightarrow {{\rm{OA}}} = 4\boldsymbol{i}\) , \(\overrightarrow {{\rm{OC}}} = 3\boldsymbol{j}\) , \(\overrightarrow {{\rm{OD}}} = 2\boldsymbol{k}\) .
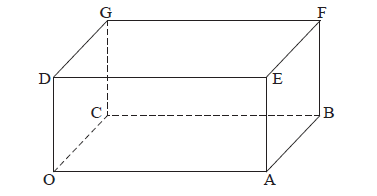
(i) Find \(\overrightarrow {{\rm{OB}}} \) .
(ii) Find \(\overrightarrow {{\rm{OF}}} \) .
(iii) Show that \(\overrightarrow {{\rm{AG}}} = – 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) .
Write down a vector equation for
(i) the line OF;
(ii) the line AG.
Find the obtuse angle between the lines OF and AG.
Answer/Explanation
Markscheme
(i) valid approach (M1)
e.g. \({\rm{OA + OB}}\)
\(\overrightarrow {{\rm{OB}}} = 4{\boldsymbol{i}} + 3{\boldsymbol{j}}\) A1 N2
(ii) valid approach (M1)
e.g. \(\overrightarrow {{\rm{OA}}} {\rm{ + }}\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{BF}}} \) ; \(\overrightarrow {{\rm{OB}}} {\rm{ + }}\overrightarrow {{\rm{BF}}} \) ; \(\overrightarrow {{\rm{OC}}} {\rm{ + }}\overrightarrow {{\rm{CG}}} {\rm{ + }}\overrightarrow {{\rm{GF}}} \)
\(\overrightarrow {{\rm{OF}}} = 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) A1 N2
(iii) correct approach A1
e.g. \(\overrightarrow {{\rm{AO}}} {\rm{ + }}\overrightarrow {{\rm{OC}}} {\rm{ + }}\overrightarrow {{\rm{CG}}} \) ; \(\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{BF}}} {\rm{ + }}\overrightarrow {{\rm{FG}}} \) ; \(\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{BC}}} {\rm{ + }}\overrightarrow {{\rm{CG}}} \)
\(\overrightarrow {{\rm{AG}}} = – 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) AG N0
[5 marks]
(i) any correct equation for (OF) in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) A2 N2
where \({\boldsymbol{a}}\) is 0 or \(4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) , and \({\boldsymbol{b}}\) is a scalar multiple of \(4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\)
e.g. \({\boldsymbol{r}} = t(4{\text{, }}3{\text{, }}2)\) , \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{4t}\\
{3t}\\
{2t}
\end{array}} \right)\) , \({\boldsymbol{r}} = 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}} + t(4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}})\)
(ii) any correct equation for (AG) in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + s{\boldsymbol{b}}\) A2 N2
where \({\boldsymbol{a}}\) is \(4{\boldsymbol{i}}\) or \(3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) and \({\boldsymbol{b}}\) is a scalar multiple of \( – 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\)
e.g. \({\boldsymbol{r}} = (4{\text{, }}0{\text{, }}0) + s( – 4{\text{, }}3{\text{, }}2)\) , \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{4 – 4s}\\
{3s}\\
{2s}
\end{array}} \right)\) , \({\boldsymbol{r}} = 3{\boldsymbol{j}} + 2{\boldsymbol{k}} + s( – 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}})\)
[4 marks]
choosing correct direction vectors, \(\overrightarrow {{\rm{OF}}} \) and \(\overrightarrow {{\rm{AG}}} \) (A1)(A1)
scalar product \( = – 16 + 9 + 4\) \(( = – 3)\) (A1)
magnitudes \(\sqrt {{4^2} + {3^2} + {2^2}} \) , \(\sqrt {{{( – 4)}^2} + {3^2} + {2^2}} \) , \(\left( {\sqrt {29} ,\sqrt {29} } \right)\) (A1)(A1)
substitution into formula M1
e.g. \(\cos \theta = \frac{{ – 16 + 9 + 4}}{{\left( {\sqrt {{4^2} + {3^2} + {2^2}} } \right) \times \sqrt {{{( – 4)}^2} + {3^2} + {2^2}} }} = \left( { – \frac{3}{{29}}} \right)\)
\(95.93777^\circ \) , \(1.67443{\text{ radians}}\)
\(\theta = 95.9^\circ \) or \(1.67\) A1 N4
[7 marks]
