Question
In the diagram below, [AB] is a diameter of the circle with centre O. Point C is on the circumference of the circle. Let \(\overrightarrow {{\text{OB}}} = \boldsymbol{b} \) and \(\overrightarrow {{\text{OC}}} = \boldsymbol{c}\) .
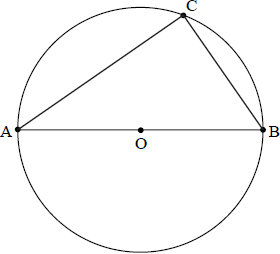
a.Find an expression for \(\overrightarrow {{\text{CB}}} \) and for \(\overrightarrow {{\text{AC}}} \) in terms of \(\boldsymbol{b}\) and \(\boldsymbol{c}\) .[2]
b.Hence prove that \({\rm{A\hat CB}}\) is a right angle. [3]
Answer/Explanation
Markscheme
a.\(\overrightarrow {{\text{CB}}} = \boldsymbol{b} – \boldsymbol{c}\) , \(\overrightarrow {{\text{AC}}} = \boldsymbol{b} + \boldsymbol{c}\) A1A1
Note: Condone absence of vector notation in (a).
[2 marks]
\(\overrightarrow {{\text{AC}}} \cdot \overrightarrow {{\text{CB}}} = \)(b + c)\( \cdot \)(b – c) M1
= \(|\)b\({|^2}\) – \(|\)c\({|^2}\) A1
= 0 since \(|\)b\(|\) = \(|\)c\(|\) R1
Note: Only award the A1 and R1 if working indicates that they understand that they are working with vectors.
so \(\overrightarrow {{\text{AC}}} \) is perpendicular to \(\overrightarrow {{\text{CB}}} \) i.e. \({\rm{A\hat CB}}\) is a right angle AG [3 marks]
Question
a.Show that the points \({\text{O}}(0,{\text{ }}0,{\text{ }}0)\), \({\text{ A}}(6,{\text{ }}0,{\text{ }}0)\), \({\text{B}}({6,{\text{ }}- \sqrt {24} ,{\text{ }}\sqrt {12} })\), \({\text{C}}({0,{\text{ }}- \sqrt {24} ,{\text{ }}\sqrt {12}})\) form a square. [3]
b.Find the coordinates of M, the mid-point of [OB].[1]
c.Show that an equation of the plane \({\mathit{\Pi }}\), containing the square OABC, is \(y + \sqrt 2 z = 0\).[3]
d.Find a vector equation of the line \(L\), through M, perpendicular to the plane \({\mathit{\Pi }}\).[3]
e.Find the coordinates of D, the point of intersection of the line \(L\) with the plane whose equation is \(y = 0\).[3]
f.Find the coordinates of E, the reflection of the point D in the plane \({\mathit{\Pi }}\).[3]
(ii) State what this tells you about the solid OABCDE. [6]
Answer/Explanation
Markscheme
a.\(\left| {\overrightarrow {{\text{OA}}} } \right| = \left| {\overrightarrow {{\text{CB}}} } \right| = \left| {\overrightarrow {{\text{OC}}} } \right| = \left| {\overrightarrow {{\text{AB}}} } \right| = 6\) (therefore a rhombus) A1A1
Note: Award A1 for two correct lengths, A2 for all four.
Note: Award A1A0 for \(\overrightarrow {{\rm{OA}}} = \overrightarrow {{\rm{CB}}} = \left( \begin{array}{l}6\\0\\0\end{array} \right){\rm{ or \,\,} } \overrightarrow {{\rm{OC}}} = \overrightarrow {A{\rm{B}}} = \left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right)\) if no magnitudes are shown.
\(\overrightarrow {{\rm{OA}}}\,\, {\rm{ g}}\overrightarrow {{\rm{OC}}} = \left( \begin{array}{l}6\\0\\0\end{array} \right){\rm{g}}\left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right) = 0 \) (therefore a square) A1
Note: Other arguments are possible with a minimum of three conditions.
[3 marks]
\({\text{M}}\left( {3,{\text{ }} – \frac{{\sqrt {24} }}{2},{\text{ }}\frac{{\sqrt {12} }}{2}} \right)\left( { = \left( {3,{\text{ }} – \sqrt 6 ,{\text{ }}\sqrt 3 } \right)} \right)\) A1
[1 mark]
METHOD 1
\(\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OC}}} = \)\(\left( \begin{array}{l}6\\0\\0\end{array} \right) \times \left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right) = \left( \begin{array}{c}0\\ – 6\sqrt {12} \\ – 6\sqrt {24} \end{array} \right)\left( { = \left( \begin{array}{c}0\\ – 12\sqrt 3 \\ – 12\sqrt 6 \end{array} \right)} \right)\) M1A1
Note: Candidates may use other pairs of vectors.
equation of plane is \( – 6\sqrt {12} y – 6\sqrt {24} z = d\)
any valid method showing that \(d = 0\) M1
\(\mathit{\Pi} :y+\sqrt{2z}=0\) AG
METHOD 2
equation of plane is \(ax + by + cz = d\)
substituting O to find \(d = 0\) (M1)
substituting two points (A, B, C or M) M1
eg
\(6a = 0,{\text{ }} – \sqrt {24} b + \sqrt {12} c = 0\) A1
\(\mathit{\Pi} :y+\sqrt{2z}=0\) AG
[3 marks]
\(\boldsymbol{r} = \left( \begin{array}{c}3\\ – \sqrt 6 \\\sqrt 3 \end{array} \right) + \lambda \left( \begin{array}{l}0\\1\\\sqrt 2 \end{array} \right)\) A1A1A1
Note: Award A1 for r = , A1A1 for two correct vectors.
[3 marks]
Using \(y = 0\) to find \(\lambda \) M1
Substitute their \(\lambda \) into their equation from part (d) M1
D has coordinates \(\left( {{\text{3, 0, 3}}\sqrt 3 } \right)\) A1
[3 marks]
\(\lambda \) for point E is the negative of the \(\lambda \) for point D (M1)
Note: Other possible methods may be seen.
E has coordinates \(\left( {{\text{3, }} – 2\sqrt 6 ,{\text{ }} – \sqrt 3 } \right)\) A1A1
Note: Award A1 for each of the y and z coordinates.
[3 marks]
(i) \(\overrightarrow {{\text{DA}}} {\text{ g}}\overrightarrow {{\text{DO}}} = \)\(\left( \begin{array}{c}3\\0\\ – 3\sqrt 3 \end{array} \right){\rm{g}}\left( \begin{array}{c} – 3\\0\\ – 3\sqrt 3 \end{array} \right) = 18\) M1A1
\(\cos {\rm{O\hat DA}} = \frac{{18}}{{\sqrt {36} \sqrt {36} }} = \frac{1}{2}\) M1
hence \({\rm{O\hat DA}} = 60^\circ \) A1
Note: Accept method showing OAD is equilateral.
(ii) OABCDE is a regular octahedron (accept equivalent description) A2
Note: A2 for saying it is made up of 8 equilateral triangles
Award A1 for two pyramids, A1 for equilateral triangles.
(can be either stated or shown in a sketch – but there must be clear indication the triangles are equilateral)
[6 marks]
Question
PQRS is a rhombus. Given that \(\overrightarrow {{\text{PQ}}} = \) \(\boldsymbol{a}\) and \(\overrightarrow {{\text{QR}}} = \) \(\boldsymbol{b}\),
(a) express the vectors \(\overrightarrow {{\text{PR}}} \) and \(\overrightarrow {{\text{QS}}} \) in terms of \(\boldsymbol{a}\) and \(\boldsymbol{b}\);
(b) hence show that the diagonals in a rhombus intersect at right angles.
Answer/Explanation
Markscheme
(a) \(\overrightarrow {{\text{PR}}} = \) a + b A1
\(\overrightarrow {{\text{QS}}} = \) b − a A1
[2 marks]
(b) \(\overrightarrow {{\text{PR}}} \cdot \overrightarrow {{\text{QS}}} = \) (a + b) \( \cdot \) (b − a) M1
\( = |\)b\({|^2} – |\)a\({|^2}\) A1
for a rhombus \(|\)a\(| = |\)b\(|\) R1
hence \(|\)b\({|^2} – |\)a\({|^2} = 0\) A1
Note: Do not award the final A1 unless R1 is awarded.
hence the diagonals intersect at right angles AG
[4 marks]
Total [6 marks]
Examiners report
Question
The position vectors of the points \(A\), \(B\) and \(C\) are \(a\), \(b\) and \(c\) respectively, relative to an origin \(O\). The following diagram shows the triangle \(ABC\) and points \(M\), \(R\), \(S\) and \(T\).
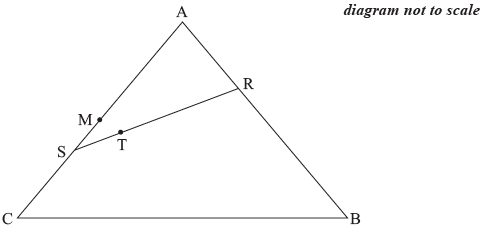
\(M\) is the midpoint of [\(AC\)].
\(R\) is a point on [\(AB\)] such that \(\overrightarrow {{\text{AR}}} = \frac{1}{3}\overrightarrow {{\text{AB}}} \).
\(S\) is a point on [\(AC\)] such that \(\overrightarrow {{\text{AS}}} = \frac{2}{3}\overrightarrow {{\text{AC}}} \).
\(T\) is a point on [\(RS\)] such that \(\overrightarrow {{\text{RT}}} = \frac{2}{3}\overrightarrow {{\text{RS}}} \).
a.(i) Express \(\overrightarrow {{\text{AM}}} \) in terms of \(a\) and \(c\).
(ii) Hence show that \(\overrightarrow {{\text{BM}}} = \frac{1}{2}\)\(a\) – \(b\)\( + \frac{1}{2}c\).[4]
b.(i) Express \(\overrightarrow {{\text{RA}}} \) in terms of \(a\) and \(b\).
(ii) Show that \(\overrightarrow {RT} = – \frac{2}{9}a – \frac{2}{9}b + \frac{4}{9}c\). [5]
c.Prove that \(T\) lies on [\(BM\)]. [5]
Answer/Explanation
Markscheme
a.(i) \(\overrightarrow {{\text{AM}}} = \frac{1}{2}\overrightarrow {{\text{AC}}} \) (M1)
\( = \frac{1}{2}\)(\(c\) – \(a\)) A1
(ii) \(\overrightarrow {{\text{BM}}} = \overrightarrow {{\text{BA}}} + \overrightarrow {{\text{AM}}} \) M1
\( = a – b + \frac{1}{2}\)\((c – a)\) A1
\(\overrightarrow {{\text{BM}}} = \frac{1}{2}a – b + \frac{1}{2}c\) AG
[4 marks]
(i) \(\overrightarrow {{\text{RA}}} = \frac{1}{3}\overrightarrow {{\text{BA}}} \)
\( = \frac{1}{3}\)(a – b) A1
(ii) \(\overrightarrow {{\text{RT}}} = \frac{2}{3}\overrightarrow {{\text{RS}}} \)
\( = \frac{2}{3}\left( {\overrightarrow {{\text{RA}}} + \overrightarrow {{\text{AS}}} } \right)\) (M1)
\( = \frac{2}{3}\left( {\frac{1}{3}(a – b) + \frac{2}{3}(c – a)} \right)\;\;\;\)or equivalent. A1A1
\( = \frac{2}{9}\)\(\left( {a – b} \right)\) \( + \frac{4}{9}\)\(\left( {c – a} \right)\) A1
\(\overrightarrow {{\text{RT}}} = – \frac{2}{9}\)\(a\) – \( – \frac{2}{9}\)\(b\) \( + \frac{4}{9}\)\(c\) AG
[5 marks]
\(\overrightarrow {{\text{BT}}} = \overrightarrow {{\text{BR}}} + \overrightarrow {{\text{RT}}} \)
\( = \frac{2}{3}\overrightarrow {{\text{BA}}} + \overrightarrow {{\text{RT}}} \) (M1)
\( = \frac{2}{3}a – \frac{2}{3}b – \frac{2}{9}a – \frac{2}{9}b + \frac{4}{9}c\) A1
\(\overrightarrow {{\text{BT}}} = \frac{8}{9}\left( {\frac{1}{2}a – b + \frac{1}{2}c} \right)\) A1
point \(B\) is common to \(\overrightarrow {{\text{BT}}} \) and \(\overrightarrow {{\text{BM}}} \) and \(\overrightarrow {{\text{BT}}} = \frac{8}{9}\overrightarrow {{\text{BM}}} \) R1R1
so \(T\) lies on [\(BM\)] AG
[5 marks] Total [14 marks]
Question
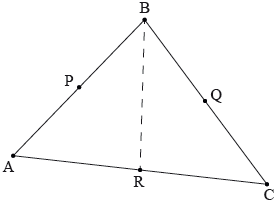
Consider the triangle \(ABC\). The points \(P\), \(Q\) and \(R\) are the midpoints of the line segments [\(AB\)], [\(BC\)] and [\(AC\)] respectively.
Let \(\overrightarrow {{\text{OA}}} = {{a}}\), \(\overrightarrow {{\text{OB}}} = {{b}}\) and \(\overrightarrow {{\text{OC}}} = {{c}}\).
a.Find \(\overrightarrow {{\text{BR}}} \) in terms of \({{a}}\), \({{b}}\) and \({{c}}\).[2]
(i) Find a vector equation of the line that passes through \(B\) and \(R\) in terms of \({{a}}\), \({{b}}\) and \({{c}}\) and a parameter \(\lambda \).
(ii) Find a vector equation of the line that passes through \(A\) and \(Q\) in terms of \({{a}}\), \({{b}}\) and \({{c}}\) and a parameter \(\mu \).
(iii) Hence show that \(\overrightarrow {{\text{OG}}} = \frac{1}{3}({{a}} + {{b}} + {{c}})\) given that \(G\) is the point where [\(BR\)] and [\(AQ\)] intersect. [9]
d. A point \(X\) is such that [\(GX\)] is perpendicular to the plane \(ABC\).
Given that the tetrahedron \(ABCX\) has volume \({\text{12 unit}}{{\text{s}}^{\text{3}}}\), find possible coordinates
of \(X\). [9]
Answer/Explanation
Markscheme
a.\(\overrightarrow {{\text{BR}}} = \overrightarrow {{\text{BA}}} + \overrightarrow {{\text{AR}}} \;\;\;\left( { = \overrightarrow {{\text{BA}}} + \frac{1}{2}\overrightarrow {{\text{AC}}} } \right)\) (M1)
\( = ({{a}} – {{b}}) + \frac{1}{2}({{c}} – {{a}})\)
\( = \frac{1}{2}{{a}} – {{b}} + \frac{1}{2}{{c}}\) A1
[2 marks]
(i) \({{\text{r}}_{{\text{BR}}}} = {{b}} + \lambda \left( {\frac{1}{2}{{a}} – {{b}} + \frac{1}{2}{{c}}} \right)\;\;\;\left( { = \frac{\lambda }{2}{{a}} + (1 – \lambda ){{b}} + \frac{\lambda }{2}{{c}}} \right)\) A1A1
Note: Award A1A0 if the \({\text{r}} = \) is omitted in an otherwise correct expression/equation.
Do not penalise such an omission more than once.
(ii) \(\overrightarrow {{\text{AQ}}} = – {{a}} + \frac{1}{2}{{b}} + \frac{1}{2}{{c}}\) (A1)
\({{\text{r}}_{{\text{AQ}}}} = {{a}} + \mu \left( { – {{a}} + \frac{1}{2}{{b}} + \frac{1}{2}{{c}}} \right)\;\;\;\left( { = (1 – \mu ){{a}} + \frac{\mu }{2}{{b}} + \frac{\mu }{2}{{c}}} \right)\) A1
Note: Accept the use of the same parameter in (i) and (ii).
(iii) when \(\overrightarrow {{\text{AQ}}} \) and \(\overrightarrow {{\text{BP}}} \) intersect we will have \({{\text{r}}_{{\text{BR}}}} = {{\text{r}}_{{\text{AQ}}}}\) (M1)
Note: If the same parameters are used for both equations, award at most M1M1A0A0M1.
\(\frac{\lambda }{2}{{a}} + (1 – \lambda ){{b}} + \frac{\lambda }{2}{{c}} = (1 – \mu ){{a}} + \frac{\mu }{2}{{b}} + \frac{\mu }{2}{{c}}\)
attempt to equate the coefficients of the vectors \({{a}}\), \({{b}}\) and \({{c}}\) M1
\(\left. {\begin{array}{*{20}{c}} {\frac{\lambda }{2} = 1 – \mu } \\ {1 – \lambda = \frac{\mu }{2}} \\ {\frac{\lambda }{2} = \frac{\mu }{2}} \end{array}} \right\}\) (A1)
\(\lambda = \frac{2}{3}\) or \(\mu = \frac{2}{3}\) A1
substituting parameters back into one of the equations M1
\(\overrightarrow {{\text{OG}}} = \frac{1}{2} \bullet \frac{2}{3}{{a}} + \left( {1 – \frac{2}{3}} \right){{b}} + \frac{1}{2} \bullet \frac{2}{3}{{c}} = \frac{1}{3}({{a}} + {{b}} + {{c}})\) AG
Note: Accept solution by verification.
[9 marks]
\(\overrightarrow {{\text{CP}}} = \frac{1}{2}{{a}} + \frac{1}{2}{{b}} – {{c}}\) (M1)A1
so we have that \({{\text{r}}_{{\text{CP}}}} = {{c}} + \beta \left( {\frac{1}{2}{{a}} + \frac{1}{2}{{b}} – {{c}}} \right)\) and when \(\beta = \frac{2}{3}\) the line passes through
the point \(G\) (ie, with position vector \(\frac{1}{3}({{a}} + {{b}} + {{c}})\)) R1
hence [\(AQ\)], [\(BR\)] and [\(CP\)] all intersect in \(G\) AG
[3 marks]
\(\overrightarrow {{\text{OG}}} = \frac{1}{3}\left( {\left( {\begin{array}{*{20}{c}} 1 \\ 3 \\ 1 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 3 \\ 7 \\ { – 5} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 2 \\ 2 \\ 1 \end{array}} \right)} \right) = \left( {\begin{array}{*{20}{c}} 2 \\ 4 \\ { – 1} \end{array}} \right)\) A1
Note: This independent mark for the vector may be awarded wherever the vector is calculated.
\(\overrightarrow {{\text{AB}}} \times \overrightarrow {{\text{AC}}} = \left( {\begin{array}{*{20}{c}} 2 \\ 4 \\ { – 6} \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} 1 \\ { – 1} \\ 0 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { – 6} \\ { – 6} \\ { – 6} \end{array}} \right)\) M1A1
\(\overrightarrow {{\text{GX}}} = \alpha \left( {\begin{array}{*{20}{c}} 1 \\ 1 \\ 1 \end{array}} \right)\) (M1)
volume of Tetrahedron given by \(\frac{1}{3} \times {\text{Area ABC}} \times {\text{GX}}\)
\( = \frac{1}{3}\left( {\frac{1}{2}\left| {\overrightarrow {{\text{AB}}} \times \overrightarrow {{\text{AC}}} } \right|} \right) \times {\text{GX}} = 12\) (M1)(A1)
Note: Accept alternative methods, for example the use of a scalar triple product.
\( = \frac{1}{6}\sqrt {{{( – 6)}^2} + {{( – 6)}^2} + {{( – 6)}^2}} \times \sqrt {{\alpha ^2} + {\alpha ^2} + {\alpha ^2}} = 12\) (A1)
\( = \frac{1}{6}6\sqrt 3 |\alpha |\sqrt 3 = 12\)
\( \Rightarrow |\alpha | = 4\) A1
Note: Condone absence of absolute value.
this gives us the position of \(X\) as \(\left( {\begin{array}{*{20}{c}} 2 \\ 4 \\ { – 1} \end{array}} \right) \pm \left( {\begin{array}{*{20}{c}} 4 \\ 4 \\ 4 \end{array}} \right)\)
\({\text{X}}(6,{\text{ }}8,{\text{ }}3)\) or \(( – 2,{\text{ }}0,{\text{ }} – 5)\) A1
Note: Award A1 for either result.
[9 marks]
Total [23 marks]
Question
O, A, B and C are distinct points such that \(\overrightarrow {{\text{OA}}} = \) a, \(\overrightarrow {{\text{OB}}} = \) b and \(\overrightarrow {{\text{OC}}} = \) c.
It is given that c is perpendicular to \(\overrightarrow {{\text{AB}}} \) and b is perpendicular to \(\overrightarrow {{\text{AC}}} \).
Prove that a is perpendicular to \(\overrightarrow {{\text{BC}}} \).
Answer/Explanation
Markscheme
c \( \bullet \) (b \( – \) a) \( = 0\) M1
Note: Allow c \( \bullet \) \(\overrightarrow {{\text{AB}}} = 0\) or similar for M1.
c \( \bullet \) b \( = \) c \( \bullet \) a A1
b \( \bullet \) (c \( – \) a) \( = 0\)
b \( \bullet \) c \( = \) b \( \bullet \) a A1
c \( \bullet \) a \( = \) b \( \bullet \) a M1
(c \( – \) b) \( \bullet \) a \( = 0\) A1
hence a is perpendicular to \(\overrightarrow {{\text{BC}}} \) AG
Note: Only award the final A1 if a dot is used throughout to indicate scalar product.
Condone any lack of specific indication that the letters represent vectors.
[5 marks]
Examiners report
This was generally poorly done. The recent syllabus change refers to ‘proof of geometrical properties using vectors’ and this is clearly a topic candidates are not entirely clear with at the moment. Despite the question clearly being written as a vector question some students tried to use a geometrical approach, assuming it was two-dimensional. Many did not seem to realise that vectors being perpendicular implies that their scalar product is zero.
Question
In the following diagram, \(\overrightarrow {{\text{OA}}} \) = a, \(\overrightarrow {{\text{OB}}} \) = b. C is the midpoint of [OA] and \(\overrightarrow {{\text{OF}}} = \frac{1}{6}\overrightarrow {{\text{FB}}} \).
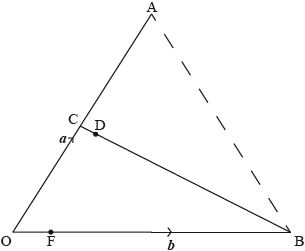
It is given also that \(\overrightarrow {{\text{AD}}} = \lambda \overrightarrow {{\text{AF}}} \) and \(\overrightarrow {{\text{CD}}} = \mu \overrightarrow {{\text{CB}}} \), where \(\lambda ,{\text{ }}\mu \in \mathbb{R}\).
Find, in terms of a and b \(\overrightarrow {{\text{OF}}} \).
Find, in terms of a and b \(\overrightarrow {{\text{AF}}} \).
Find an expression for \(\overrightarrow {{\text{OD}}} \) in terms of a, b and \(\lambda \);
Find an expression for \(\overrightarrow {{\text{OD}}} \) in terms of a, b and \(\mu \).
Show that \(\mu = \frac{1}{{13}}\), and find the value of \(\lambda \).
Deduce an expression for \(\overrightarrow {{\text{CD}}} \) in terms of a and b only.
Given that area \(\Delta {\text{OAB}} = k({\text{area }}\Delta {\text{CAD}})\), find the value of \(k\).
Answer/Explanation
Markscheme
\(\overrightarrow {{\text{OF}}} = \frac{1}{7}\)b A1
[1 mark]
\(\overrightarrow {{\text{AF}}} = \overrightarrow {{\text{OF}}} – \overrightarrow {{\text{OA}}} \) (M1)
\( = \frac{1}{7}\)b – a A1
[2 marks]
\(\overrightarrow {{\text{OD}}} = \) a \( + \lambda \left( {\frac{1}{7}b -a} \right){\text{ }}\left( { = (1 – \lambda )a + \frac{\lambda }{7}b} \right)\) M1A1
[2 marks]
\(\overrightarrow {{\text{OD}}} = \frac{1}{2}\) a \( + \mu \left( { – \frac{1}{2}a + b} \right){\text{ }}\left( { = \left( {\frac{1}{2} – \frac{\mu }{2}} \right)a + \mu b} \right)\) M1A1
[2 marks]
equating coefficients: M1
\(\frac{\lambda }{7} = \mu ,{\text{ }}1 – \lambda = \frac{{1 – \mu }}{2}\) A1
solving simultaneously: M1
\(\lambda = \frac{7}{{13}},{\text{ }}\mu = \frac{1}{{13}}\) A1AG
[4 marks]
\(\overrightarrow {{\text{CD}}} = \frac{1}{{13}}\overrightarrow {{\text{CB}}} \)
\( = \frac{1}{{13}}\left( {b – \frac{1}{2}a} \right){\text{ }}\left( { = – \frac{1}{{26}}a + \frac{1}{{13}}b} \right)\) M1A1
[2 marks]
METHOD 1
\({\text{area }}\Delta {\text{ACD}} = \frac{1}{2}{\text{CD}} \times {\text{AC}} \times \sin {\rm{A\hat CB}}\) (M1)
\({\text{area }}\Delta {\text{ACB}} = \frac{1}{2}{\text{CB}} \times {\text{AC}} \times \sin {\rm{A\hat CB}}\) (M1)
\({\text{ratio }}\frac{{{\text{area }}\Delta {\text{ACD}}}}{{{\text{area }}\Delta {\text{ACB}}}} = \frac{{{\text{CD}}}}{{{\text{CB}}}} = \frac{1}{{13}}\) A1
\(k = \frac{{{\text{area }}\Delta {\text{OAB}}}}{{{\text{area }}\Delta {\text{CAD}}}} = \frac{{13}}{{{\text{area }}\Delta {\text{CAB}}}} \times {\text{area }}\Delta {\text{OAB}}\) (M1)
\( = 13 \times 2 = 26\) A1
METHOD 2
\({\text{area }}\Delta {\text{OAB}} = \frac{1}{2}\left| {a \times b} \right|\) A1
\({\text{area }}\Delta {\text{CAD}} = \frac{1}{2}\left| {\overrightarrow {{\text{CA}}} \times \overrightarrow {{\text{CD}}} } \right|\) or \(\frac{1}{2}\left| {\overrightarrow {{\text{CA}}} \times \overrightarrow {{\text{AD}}} } \right|\) M1
\( = \frac{1}{2}\left| {\frac{1}{2}a \times \left( { – \frac{1}{{26}}a + \frac{1}{{13}}b} \right)} \right|\)
\( = \frac{1}{2}\left| {\frac{1}{2}a \times \left( { – \frac{1}{{26}}a} \right) + \frac{1}{2}a \times \frac{1}{{13}}b} \right|\) (M1)
\( = \frac{1}{2} \times \frac{1}{2} \times \frac{1}{{13}}\left| {a \times b} \right|{\text{ }}\left( { = \frac{1}{{52}}\left| {a \times b} \right|} \right)\) A1
\({\text{area }}\Delta {\text{OAB}} = k({\text{area }}\Delta {\text{CAD}})\)
\(\frac{1}{2}\left| {a \times b} \right| = k\frac{1}{{52}}\left| {a \times b} \right|\)
\(k = 26\) A1
[5 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
The points A, B, C and D have position vectors a, b, c and d, relative to the origin O.
It is given that \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \).
The position vectors \(\mathop {{\text{OA}}}\limits^ \to \), \(\mathop {{\text{OB}}}\limits^ \to \), \(\mathop {{\text{OC}}}\limits^ \to \) and \(\mathop {{\text{OD}}}\limits^ \to \) are given by
a = i + 2j − 3k
b = 3i − j + pk
c = qi + j + 2k
d = −i + rj − 2k
where p , q and r are constants.
The point where the diagonals of ABCD intersect is denoted by M.
The plane \(\Pi \) cuts the x, y and z axes at X , Y and Z respectively.
Explain why ABCD is a parallelogram.
Using vector algebra, show that \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \).
Show that p = 1, q = 1 and r = 4.
Find the area of the parallelogram ABCD.
Find the vector equation of the straight line passing through M and normal to the plane \(\Pi \) containing ABCD.
Find the Cartesian equation of \(\Pi \).
Find the coordinates of X, Y and Z.
Find YZ.
Answer/Explanation
Markscheme
a pair of opposite sides have equal length and are parallel R1
hence ABCD is a parallelogram AG
[1 mark]
attempt to rewrite the given information in vector form M1
b − a = c − d A1
rearranging d − a = c − b M1
hence \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) AG
Note: Candidates may correctly answer part i) by answering part ii) correctly and then deducing there
are two pairs of parallel sides.
[3 marks]
EITHER
use of \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
2 \hfill \\
– 3 \hfill \\
p + 3 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q + 1 \hfill \\
1 – r \hfill \\
4 \hfill \\
\end{gathered} \right)\) A1A1
OR
use of \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
– 2 \hfill \\
r – 2 \hfill \\
1 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q – 3 \hfill \\
2 \hfill \\
2 – p \hfill \\
\end{gathered} \right)\) A1A1
THEN
attempt to compare coefficients of i, j, and k in their equation or statement to that effect M1
clear demonstration that the given values satisfy their equation A1
p = 1, q = 1, r = 4 AG
[5 marks]
attempt at computing \(\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to \) (or equivalent) M1
\(\left( \begin{gathered}
– 11 \hfill \\
– 10 \hfill \\
– 2 \hfill \\
\end{gathered} \right)\) A1
area \( = \left| {\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to } \right|\left( { = \sqrt {225} } \right)\) (M1)
= 15 A1
[4 marks]
valid attempt to find \(\mathop {{\text{OM}}}\limits^ \to = \left( {\frac{1}{2}\left( {a + c} \right)} \right)\) (M1)
\(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right)\) A1
the equation is
r = \(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
11 \hfill \\
10 \hfill \\
2 \hfill \\
\end{gathered} \right)\) or equivalent M1A1
Note: Award maximum M1A0 if ‘r = …’ (or equivalent) is not seen.
[4 marks]
attempt to obtain the equation of the plane in the form ax + by + cz = d M1
11x + 10y + 2z = 25 A1A1
Note: A1 for right hand side, A1 for left hand side.
[3 marks]
putting two coordinates equal to zero (M1)
\({\text{X}}\left( {\frac{{25}}{{11}},\,0,\,0} \right),\,\,{\text{Y}}\left( {0,\,\frac{5}{2},\,0} \right),\,\,{\text{Z}}\left( {0,\,0,\,\frac{{25}}{2}} \right)\) A1
[2 marks]
\({\text{YZ}} = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{25}}{2}} \right)}^2}} \) M1
\( = \sqrt {\frac{{325}}{2}} \left( { = \frac{{5\sqrt {104} }}{4} = \frac{{5\sqrt {26} }}{2}} \right)\) A1
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
