Question
Consider the points A (1 , 5 , 4) , B (3 , 1 , 2) and D (3 , k , 2) , with (AD) perpendicular to (AB) .
The point O has coordinates (0 , 0 , 0) , point A has coordinates (1 , – 2 , 3) and point B has coordinates (– 3 , 4 , 2) .
Find
(i) \(\overrightarrow {{\rm{AB}}} \) ;
(ii) \(\overrightarrow {{\rm{AD}}} \) giving your answer in terms of k .
[3 marks]
Show that \(k = 7\) .
The point C is such that \(\overrightarrow {{\rm{BC}}} = \frac{1}{2}\overrightarrow {{\rm{AD}}} \) .
Find the position vector of C.
Find \(\cos {\rm{A}}\widehat {\rm{B}}{\rm{C}}\) .
Answer/Explanation
Markscheme
(i) evidence of combining vectors (M1)
e.g. \(\overrightarrow {{\rm{AB}}} = \overrightarrow {{\rm{OB}}} – \overrightarrow {{\rm{OA}}} \) (or \(\overrightarrow {{\rm{AD}}} = \overrightarrow {{\rm{AO}}} + \overrightarrow {{\rm{OD}}} \) in part (ii))
\(\overrightarrow {{\rm{AB}}} = \left( {\begin{array}{*{20}{c}}
2\\
{ – 4}\\
{ – 2}
\end{array}} \right)\) A1 N2
(ii) \(\overrightarrow {{\rm{AD}}} = \left( {\begin{array}{*{20}{c}}
2\\
{k – 5}\\
{ – 2}
\end{array}} \right)\) A1 N1
[3 marks]
evidence of using perpendicularity \( \Rightarrow \) scalar product = 0 (M1)
e.g. \(\left( {\begin{array}{*{20}{c}}
2\\
{ – 4}\\
{ – 2}
\end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}}
2\\
{k – 5}\\
{ – 2}
\end{array}} \right) = 0\)
\(4 – 4(k – 5) + 4 = 0\) A1
\( – 4k + 28 = 0\) (accept any correct equation clearly leading to \(k = 7\) ) A1
\(k = 7\) AG N0
[3 marks]
\(\overrightarrow {{\rm{AD}}} = \left( {\begin{array}{*{20}{c}}
2\\
2\\
{ – 2}
\end{array}} \right)\) (A1)
\(\overrightarrow {{\rm{BC}}} = \left( {\begin{array}{*{20}{c}}
1\\
1\\
{ – 1}
\end{array}} \right)\) A1
evidence of correct approach (M1)
e.g. \(\overrightarrow {{\rm{OC}}} = \overrightarrow {{\rm{OB}}} + \overrightarrow {{\rm{BC}}} \) , \(\left( {\begin{array}{*{20}{c}}
3\\
1\\
2
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
1\\
1\\
{ – 1}
\end{array}} \right)\) , \(\left( {\begin{array}{*{20}{c}}
{x – 3}\\
{y – 1}\\
{z – 2}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1\\
1\\
{ – 1}
\end{array}} \right)\)
\(\overrightarrow {{\rm{OC}}} = \left( {\begin{array}{*{20}{c}}
4\\
2\\
1
\end{array}} \right)\) A1 N3
[4 marks]
METHOD 1
choosing appropriate vectors, \(\overrightarrow {{\rm{BA}}} \) , \(\overrightarrow {{\rm{BC}}} \) (A1)
finding the scalar product M1
e.g. \( – 2(1) + 4(1) + 2( – 1)\) , \(2(1) + ( – 4)(1) + ( – 2)( – 1)\)
\(\cos {\rm{A}}\widehat {\rm{B}}{\rm{C = 0}}\) A1 N1
METHOD 2
\(\overrightarrow {{\rm{BC}}} \) parallel to \(\overrightarrow {{\rm{AD}}} \) (may show this on a diagram with points labelled) R1
\(\overrightarrow {{\rm{BC}}} \bot \overrightarrow {{\rm{AB}}} \) (may show this on a diagram with points labelled) R1
\({\rm{A}}\widehat {\rm{B}}{\rm{C}} = 90^\circ \)
\(\cos {\rm{A}}\widehat {\rm{B}}{\rm{C = 0}}\) A1 N1
[3 marks]
Question
The vertices of the triangle PQR are defined by the position vectors
\(\overrightarrow {{\rm{OP}}} = \left( {\begin{array}{*{20}{c}}
4\\
{ – 3}\\
1
\end{array}} \right)\) , \(\overrightarrow {{\rm{OQ}}} = \left( {\begin{array}{*{20}{c}}
3\\
{ – 1}\\
2
\end{array}} \right)\) and \(\overrightarrow {{\rm{OR}}} = \left( {\begin{array}{*{20}{c}}
6\\
{ – 1}\\
5
\end{array}} \right)\) .
Find
(i) \(\overrightarrow {{\rm{PQ}}} \) ;
(ii) \(\overrightarrow {{\rm{PR}}} \) .
Show that \(\cos {\rm{R}}\widehat {\rm{P}}{\rm{Q}} = \frac{1}{2}\) .
(i) Find \({\rm{sinR}}\widehat {\rm{P}}{\rm{Q}}\) .
(ii) Hence, find the area of triangle PQR, giving your answer in the form \(a\sqrt 3 \) .
Answer/Explanation
Markscheme
(i) evidence of approach (M1)
e.g. \(\overrightarrow {{\rm{PQ}}} = \overrightarrow {{\rm{PO}}} + \overrightarrow {{\rm{OQ}}} \) , \({\rm{Q}} – {\rm{P}}\)
\(\overrightarrow {{\rm{PQ}}} = \left( {\begin{array}{*{20}{c}}
{ – 1}\\
2\\
1
\end{array}} \right)\) A1 N2
(ii) \(\overrightarrow {{\rm{PR}}} = \left( {\begin{array}{*{20}{c}}
2\\
2\\
4
\end{array}} \right)\) A1 N1
[3 marks]
METHOD 1
choosing correct vectors \(\overrightarrow {{\rm{PQ}}} \) and \(\overrightarrow {{\rm{PR}}} \) (A1)(A1)
finding \(\overrightarrow {{\rm{PQ}}} \bullet \overrightarrow {{\rm{PR}}} \) , \(\left| {\overrightarrow {{\rm{PQ}}} } \right|\) , \(\left| {\overrightarrow {{\rm{PR}}} } \right|\) (A1) (A1)(A1)
\(\overrightarrow {{\rm{PQ}}} \bullet \overrightarrow {{\rm{PR}}} = – 2 + 4 + 4( = 6)\)
\(\left| {\overrightarrow {{\rm{PQ}}} } \right| = \sqrt {{{( – 1)}^2} + {2^2} + {1^2}} \) \(\left( { = \sqrt 6 } \right)\) , \(\left| {\overrightarrow {{\rm{PR}}} } \right| = \sqrt {{2^2} + {2^2} + {4^2}} \) \(\left( { = \sqrt {24} } \right)\)
substituting into formula for angle between two vectors M1
e.g. \(\cos {\rm{R}}\widehat {\rm{P}}{\rm{Q}} = \frac{6}{{\sqrt 6 \times \sqrt {24} }}\)
simplifying to expression clearly leading to \(\frac{1}{2}\) A1
e.g. \(\frac{6}{{\sqrt 6 \times 2\sqrt 6 }}\) , \(\frac{6}{{\sqrt {144} }}\) , \(\frac{6}{{12}}\)
\(\cos {\rm{R}}\widehat {\rm{P}}{\rm{Q}} = \frac{1}{2}\) AG N0
METHOD 2
evidence of choosing cosine rule (seen anywhere) (M1)
\(\overrightarrow {{\rm{QR}}} = \left( {\begin{array}{*{20}{c}}
3\\
0\\
3
\end{array}} \right)\) A1
\(\left| {\overrightarrow {{\rm{QR}}} } \right| = \sqrt {18} \) , \(\left| {\overrightarrow {{\rm{PQ}}} } \right| = \sqrt 6 \) and \(\left| {\overrightarrow {{\rm{PR}}} } \right| = \sqrt {24} \) (A1)(A1)(A1)
\(\cos {\rm{R}}\widehat {\rm{P}}{\rm{Q}} = \frac{{{{\left( {\sqrt 6 } \right)}^2} + {{\left( {\sqrt {24} } \right)}^2} – {{\left( {\sqrt {18} } \right)}^2}}}{{2\sqrt 6 \times \sqrt {24} }}\) A1
\(\cos {\rm{R}}\widehat {\rm{P}}{\rm{Q}} = \frac{{6 + 24 – 18}}{{24}}\) \(\left( { = \frac{{12}}{{24}}} \right)\) A1
\(\cos {\rm{R}}\widehat {\rm{P}}{\rm{Q}} = \frac{1}{2}\) AG N0
[7 marks]
(i) METHOD 1
evidence of appropriate approach (M1)
e.g. using \({\rm{si}}{{\rm{n}}^{\rm{2}}}{\rm{R}}\widehat {\rm{P}}{\rm{Q + co}}{{\rm{s}}^{\rm{2}}}{\rm{R}}\widehat {\rm{P}}{\rm{Q}} = 1\) , diagram
substituting correctly (A1)
e.g. \({\rm{sinR}}\widehat {\rm{P}}{\rm{Q}} = \sqrt {1 – {{\left( {\frac{1}{2}} \right)}^2}} \)
\({\rm{sinR}}\widehat {\rm{P}}{\rm{Q}} = \sqrt {\frac{3}{4}} \) \(\left( { = \frac{{\sqrt 3 }}{2}} \right)\) A1 N3
METHOD 2
since \(\cos \widehat {\rm{P}} = \frac{1}{2}\) , \(\widehat {\rm{P}} = 60^\circ \) (A1)
evidence of approach
e.g. drawing a right triangle, finding the missing side (A1)
\(\sin \widehat {\rm{P}} = \frac{{\sqrt 3 }}{2}\) A1 N3
(ii) evidence of appropriate approach (M1)
e.g. attempt to substitute into \(\frac{1}{2}ab\sin C\)
correct substitution
e.g. area \( = \frac{1}{2}\sqrt 6 \times \sqrt {24} \times \frac{{\sqrt 3 }}{2}\) A1
area \( = 3\sqrt 3 \) A1 N2
[6 marks]
Question
The line \({L_1}\) is parallel to the z-axis. The point P has position vector \(\left( {\begin{array}{*{20}{c}}
8\\
1\\
0
\end{array}} \right)\) and lies on \({L_1}\).
Write down the equation of \({L_1}\) in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\).
The line \({L_2}\) has equation \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
2\\
4\\
{ – 1}
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right)\) . The point A has position vector \(\left( {\begin{array}{*{20}{c}}
6\\
2\\
9
\end{array}} \right)\) .
Show that A lies on \({L_2}\) .
Let B be the point of intersection of lines \({L_1}\) and \({L_2}\) .
(i) Show that \(\overrightarrow {{\rm{OB}}} = \left( {\begin{array}{*{20}{c}}
8\\
1\\
{14}
\end{array}} \right)\) .
(ii) Find \(\overrightarrow {{\rm{AB}}} \) .
The point C is at (2, 1, − 4). Let D be the point such that ABCD is a parallelogram.
Find \(\overrightarrow {{\rm{OD}}} \) .
Answer/Explanation
Markscheme
\({L_1}:{\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
8\\
1\\
0
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
0\\
0\\
1
\end{array}} \right)\) A2 N2
[2 marks]
evidence of equating \({\boldsymbol{r}}\) and \(\overrightarrow {{\rm{OA}}} \) (M1)
e.g. \(\left( {\begin{array}{*{20}{c}}
6\\
2\\
9
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
2\\
4\\
{ – 1}
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right)\) , \(A = r\)
one correct equation A1
e.g. \(6 = 2 + 2s\) , \(2 = 4 – s\) , \(9 = – 1 + 5s\)
\(s = 2\) A1
evidence of confirming for other two equations A1
e.g. \(6 = 2 + 4\) , \(2 = 4 – 2\) , \(9 = – 1 + 10\)
so A lies on \({L_2}\) AG N0
[4 marks]
(i) evidence of approach M1
e.g. \(\left( {\begin{array}{*{20}{c}}
2\\
4\\
{ – 1}
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
8\\
1\\
0
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
0\\
0\\
1
\end{array}} \right)\) \({L_1} = {L_2}\)
one correct equation A1
e.g. \(2 + 2s = 8\) , \(4 – s = 1\) , \( – 1 + 5s = t\)
attempt to solve (M1)
finding \(s = 3\) A1
substituting M1
e.g. \(\overrightarrow {{\rm{OB}}} = \left( {\begin{array}{*{20}{c}}
2\\
4\\
{ – 1}
\end{array}} \right) + 3\left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right)\)
\(\overrightarrow {{\rm{OB}}} = \left( {\begin{array}{*{20}{c}}
8\\
1\\
{14}
\end{array}} \right)\) AG N0
(ii) evidence of appropriate approach (M1)
e.g. \(\overrightarrow {{\rm{AB}}} = \overrightarrow {{\rm{AO}}} + \overrightarrow {{\rm{OB}}} \) , \(\overrightarrow {{\rm{AB}}} = \overrightarrow {{\rm{OB}}} – \overrightarrow {{\rm{OA}}} \)
\(\overrightarrow {{\rm{AB}}} = \left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right)\) A1 N2
[7 marks]
evidence of appropriate approach (M1)
e.g. \(\overrightarrow {{\rm{AB}}} = \overrightarrow {{\rm{DC}}} \)
correct values A1
e.g. \(\overrightarrow {{\rm{OD}}} + \left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
2\\
1\\
{ – 4}
\end{array}} \right)\) , \(\left( {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
2\\
1\\
{ – 4}
\end{array}} \right)\) , \(\left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{2 – x}\\
{1 – y}\\
{ – 4 – z}
\end{array}} \right)\)
\(\overrightarrow {{\rm{OD}}} = \left( {\begin{array}{*{20}{c}}
0\\
2\\
{ – 9}
\end{array}} \right)\) A1 N2
[3 marks]
Question
Consider the vectors \(\boldsymbol{a} = \left( {\begin{array}{*{20}{c}}
2\\
{ – 3}
\end{array}} \right)\) and \(\boldsymbol{b} = \left( {\begin{array}{*{20}{c}}
1\\
4
\end{array}} \right)\) .
Let \(2\boldsymbol{a} + \boldsymbol{b} + \boldsymbol{c} = 0\) , where \(0\) is the zero vector.
(a) Find
(i) \(2\boldsymbol{a} + \boldsymbol{b}\) ;
(ii) \(\left| {2\boldsymbol{a} + \boldsymbol{b}} \right|\) .
Let \(2\boldsymbol{a} + \boldsymbol{b} + \boldsymbol{c} = 0\) , where \(0\) is the zero vector.
(b) Find \(\boldsymbol{c}\) .
Find
(i) \(2\boldsymbol{a} + \boldsymbol{b}\) ;
(ii) \(\left| {2\boldsymbol{a} + \boldsymbol{b}} \right|\) .
Find \(\boldsymbol{c}\) .
Answer/Explanation
Markscheme
(a) (i) \(2\boldsymbol{a} = \left( {\begin{array}{*{20}{c}}
4\\
{ – 6}
\end{array}} \right)\) (A1)
correct expression for \(2\boldsymbol{a} + \boldsymbol{b}\) A1 N2
eg \(\left( {\begin{array}{*{20}{c}}
5\\
{ – 2}
\end{array}} \right)\) , \((5, – 2)\) , \(5\boldsymbol{i} – 2\boldsymbol{j}\)
(ii) correct substitution into length formula (A1)
eg \(\sqrt {{5^2} + {2^2}} \) , \(\sqrt {{5^2} + – {2^2}} \)
\(\left| {2\boldsymbol{a} + \boldsymbol{b}} \right| = \sqrt {29} \) A1 N2
[4 marks]
(b) valid approach (M1)
eg \(\boldsymbol{c} = – (2\boldsymbol{a} + \boldsymbol{b})\) , \(5 + x = 0\) , \( – 2 + y = 0\)
\(\boldsymbol{c} = \left( {\begin{array}{*{20}{c}}
{ – 5}\\
2
\end{array}} \right)\) A1 N2
[2 marks]
(i) \(2\boldsymbol{a} = \left( {\begin{array}{*{20}{c}}
4\\
{ – 6}
\end{array}} \right)\) (A1)
correct expression for \(2\boldsymbol{a} + \boldsymbol{b}\) A1 N2
eg \(\left( {\begin{array}{*{20}{c}}
5\\
{ – 2}
\end{array}} \right)\) , \((5, – 2)\) , \(5\boldsymbol{i} – 2\boldsymbol{j}\)
(ii) correct substitution into length formula (A1)
eg \(\sqrt {{5^2} + {2^2}} \) , \(\sqrt {{5^2} + – {2^2}} \)
\(\left| {2\boldsymbol{a} + \boldsymbol{b}} \right| = \sqrt {29} \) A1 N2
[4 marks]
valid approach (M1)
eg \(\boldsymbol{c} = – (2\boldsymbol{a} + \boldsymbol{b})\) , \(5 + x = 0\) , \( – 2 + y = 0\)
\(\boldsymbol{c} = \left( {\begin{array}{*{20}{c}}
{ – 5}\\
2
\end{array}} \right)\) A1 N2
[2 marks]
Question
In the following diagram, \(\boldsymbol{u} = \overrightarrow {{\rm{AB}}} \) and \(\boldsymbol{v} = \overrightarrow {{\rm{BD}}} \) .
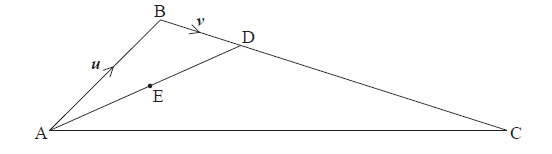
The midpoint of \(\overrightarrow {{\rm{AD}}} \) is E and \(\frac{{{\rm{BD}}}}{{{\rm{DC}}}} = \frac{1}{3}\) .
Express each of the following vectors in terms of \(\boldsymbol{u}\) and \(\boldsymbol{v}\) .
\(\overrightarrow {{\rm{AE}}} \)
\(\overrightarrow {{\rm{EC}}} \)
Answer/Explanation
Markscheme
\(\overrightarrow {{\rm{AE}}} = \frac{1}{2}\overrightarrow {{\rm{AD}}} \) A1
attempt to find \(\overrightarrow {{\rm{AD}}} \) M1
e.g. \(\overrightarrow {{\rm{AB}}} + \overrightarrow {{\rm{BD}}} \) , \({\boldsymbol{u}} + {\boldsymbol{v}}\)
\(\overrightarrow {{\rm{AE}}} = \frac{1}{2}(u + v)\) \(\left( { = \frac{1}{2}{\boldsymbol{u}} + \frac{1}{2}{\boldsymbol{v}}} \right)\) A1 N2
[3 marks]
\(\overrightarrow {{\rm{EC}}} = \overrightarrow {{\rm{AE}}} = \frac{1}{2}({\boldsymbol{u}} + {\boldsymbol{v}})\) A1
\(\overrightarrow {{\rm{DC}}} = 3{\boldsymbol{v}}\) A1
attempt to find \(\overrightarrow {{\rm{EC}}} \) M1
e.g. \(\overrightarrow {{\rm{ED}}} + \overrightarrow {{\rm{DC}}} \) , \(\frac{1}{2}({\boldsymbol{u}} + {\boldsymbol{v}}) + 3{\boldsymbol{v}}\)
\(\overrightarrow {{\rm{EC}}} = \frac{1}{2}{\boldsymbol{u}} + \frac{7}{2}{\boldsymbol{v}}\) \(\left( { = \frac{1}{2}({\boldsymbol{u}} + 7{\boldsymbol{v}})} \right)\) A1 N2
[4 marks]

