Question
A particle is moving with a constant velocity along line L . Its initial position is A(6 , −2 , 10) . After one second the particle has moved to B( 9, −6 , 15) .
(i) Find the velocity vector, \(\overrightarrow {{\rm{AB}}} \) .
(ii) Find the speed of the particle.
Write down an equation of the line L .
Answer/Explanation
Markscheme
(i) evidence of approach (M1)
e.g. \(\overrightarrow {{\rm{AO}}} + \overrightarrow {{\rm{OB}}} \) , \({\rm{B}} – {\rm{A}}\) , \(\left( {\begin{array}{*{20}{c}}
{9 – 6}\\
{ – 6 + 2}\\
{15 – 10}
\end{array}} \right)\)
\(\overrightarrow {{\rm{AB}}} = \left( {\begin{array}{*{20}{c}}
3\\
{ – 4}\\
5
\end{array}} \right)\) (accept \(\left( {3, – 4, 5} \right)\) ) A1 N2
(ii) evidence of finding the magnitude of the velocity vector M1
e.g. \({\text{speed}} = \sqrt {{3^2} + {4^2} + {5^2}} \)
\({\text{speed}} = \sqrt {50} \) \(\left( { = 5\sqrt 2 } \right)\) A1 N1
[4 marks]
correct equation (accept Cartesian and parametric forms) A2 N2
e.g. \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
6\\
{ – 2}\\
{10}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
3\\
{ – 4}\\
5
\end{array}} \right)\) , \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
9\\
{ – 6}\\
{15}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
3\\
{ – 4}\\
5
\end{array}} \right)\)
[2 marks]
Question
The line \({L_1}\) is parallel to the z-axis. The point P has position vector \(\left( {\begin{array}{*{20}{c}}
8\\
1\\
0
\end{array}} \right)\) and lies on \({L_1}\).
Write down the equation of \({L_1}\) in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\).
The line \({L_2}\) has equation \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
2\\
4\\
{ – 1}
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right)\) . The point A has position vector \(\left( {\begin{array}{*{20}{c}}
6\\
2\\
9
\end{array}} \right)\) .
Show that A lies on \({L_2}\) .
Let B be the point of intersection of lines \({L_1}\) and \({L_2}\) .
(i) Show that \(\overrightarrow {{\rm{OB}}} = \left( {\begin{array}{*{20}{c}}
8\\
1\\
{14}
\end{array}} \right)\) .
(ii) Find \(\overrightarrow {{\rm{AB}}} \) .
The point C is at (2, 1, − 4). Let D be the point such that ABCD is a parallelogram.
Find \(\overrightarrow {{\rm{OD}}} \) .
Answer/Explanation
Markscheme
\({L_1}:{\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
8\\
1\\
0
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
0\\
0\\
1
\end{array}} \right)\) A2 N2
[2 marks]
evidence of equating \({\boldsymbol{r}}\) and \(\overrightarrow {{\rm{OA}}} \) (M1)
e.g. \(\left( {\begin{array}{*{20}{c}}
6\\
2\\
9
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
2\\
4\\
{ – 1}
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right)\) , \(A = r\)
one correct equation A1
e.g. \(6 = 2 + 2s\) , \(2 = 4 – s\) , \(9 = – 1 + 5s\)
\(s = 2\) A1
evidence of confirming for other two equations A1
e.g. \(6 = 2 + 4\) , \(2 = 4 – 2\) , \(9 = – 1 + 10\)
so A lies on \({L_2}\) AG N0
[4 marks]
(i) evidence of approach M1
e.g. \(\left( {\begin{array}{*{20}{c}}
2\\
4\\
{ – 1}
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
8\\
1\\
0
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
0\\
0\\
1
\end{array}} \right)\) \({L_1} = {L_2}\)
one correct equation A1
e.g. \(2 + 2s = 8\) , \(4 – s = 1\) , \( – 1 + 5s = t\)
attempt to solve (M1)
finding \(s = 3\) A1
substituting M1
e.g. \(\overrightarrow {{\rm{OB}}} = \left( {\begin{array}{*{20}{c}}
2\\
4\\
{ – 1}
\end{array}} \right) + 3\left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right)\)
\(\overrightarrow {{\rm{OB}}} = \left( {\begin{array}{*{20}{c}}
8\\
1\\
{14}
\end{array}} \right)\) AG N0
(ii) evidence of appropriate approach (M1)
e.g. \(\overrightarrow {{\rm{AB}}} = \overrightarrow {{\rm{AO}}} + \overrightarrow {{\rm{OB}}} \) , \(\overrightarrow {{\rm{AB}}} = \overrightarrow {{\rm{OB}}} – \overrightarrow {{\rm{OA}}} \)
\(\overrightarrow {{\rm{AB}}} = \left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right)\) A1 N2
[7 marks]
evidence of appropriate approach (M1)
e.g. \(\overrightarrow {{\rm{AB}}} = \overrightarrow {{\rm{DC}}} \)
correct values A1
e.g. \(\overrightarrow {{\rm{OD}}} + \left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
2\\
1\\
{ – 4}
\end{array}} \right)\) , \(\left( {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
2\\
1\\
{ – 4}
\end{array}} \right)\) , \(\left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{2 – x}\\
{1 – y}\\
{ – 4 – z}
\end{array}} \right)\)
\(\overrightarrow {{\rm{OD}}} = \left( {\begin{array}{*{20}{c}}
0\\
2\\
{ – 9}
\end{array}} \right)\) A1 N2
[3 marks]
Question
The line \({L_1}\) is represented by the vector equation \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{ – 3}\\
{ – 1}\\
{ – 25}
\end{array}} \right) + p\left( {\begin{array}{*{20}{c}}
2\\
1\\
{ – 8}
\end{array}} \right)\) .
A second line \({L_2}\) is parallel to \({L_1}\) and passes through the point B(\( – 8\), \( – 5\), \(25\)) .
Write down a vector equation for \({L_2}\) in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) .
A third line \({L_3}\) is perpendicular to \({L_1}\) and is represented by \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
5\\
0\\
3
\end{array}} \right) + q\left( {\begin{array}{*{20}{c}}
{ – 7}\\
{ – 2}\\
k
\end{array}} \right)\) .
Show that \(k = – 2\) .
The lines \({L_1}\) and \({L_3}\) intersect at the point A.
Find the coordinates of A.
The lines \({L_2}\)and \({L_3}\)intersect at point C where \(\overrightarrow {{\rm{BC}}} = \left( {\begin{array}{*{20}{c}}
6\\
3\\
{ – 24}
\end{array}} \right)\) .
(i) Find \(\overrightarrow {{\rm{AB}}} \) .
(ii) Hence, find \(|\overrightarrow {{\rm{AC}}} |\) .
Answer/Explanation
Markscheme
any correct equation in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) (accept any parameter) A2 N2
e.g. \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{ – 8}\\
{ – 5}\\
{25}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
2\\
1\\
{ – 8}
\end{array}} \right)\)
Note: Award A1 for \({\boldsymbol{a}} + t{\boldsymbol{b}}\) , A1 for \(L = {\boldsymbol{a}} + t{\boldsymbol{b}}\) , A0 for \({\boldsymbol{r}} = {\boldsymbol{b}} + t{\boldsymbol{a}}\) .
[2 marks]
recognizing scalar product must be zero (seen anywhere) R1
e.g. \({\boldsymbol{a}} \bullet {\boldsymbol{b}} = 0\)
evidence of choosing direction vectors \(\left( {\begin{array}{*{20}{c}}
2\\
1\\
{ – 8}
\end{array}} \right),\left( {\begin{array}{*{20}{c}}
{ – 7}\\
{ – 2}\\
k
\end{array}} \right)\) (A1)(A1)
correct calculation of scalar product (A1)
e.g. \(2( – 7) + 1( – 2) – 8k\)
simplification that clearly leads to solution A1
e.g. \( – 16 – 8k\) , \( – 16 – 8k = 0\)
\(k = – 2\) AG N0
[5 marks]
evidence of equating vectors (M1)
e.g. \({L_1} = {L_3}\) , \(\left( {\begin{array}{*{20}{c}}
{ – 3}\\
{ – 1}\\
{ – 25}
\end{array}} \right) + p\left( {\begin{array}{*{20}{c}}
2\\
1\\
{ – 8}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
5\\
0\\
3
\end{array}} \right) + q\left( {\begin{array}{*{20}{c}}
{ – 7}\\
{ – 2}\\
{ – 2}
\end{array}} \right)\)
any two correct equations A1A1
e.g. \( – 3 + 2p = 5 – 7q\) , \( – 1 + p = – 2q\) , \(- 25 – 8p = 3 – 2q\)
attempting to solve equations (M1)
finding one correct parameter (\(p = – 3\) , \(q = 2\) ) A1
the coordinates of A are \(( – 9, – 4, – 1)\) A1 N3
[6 marks]
(i) evidence of appropriate approach (M1)
e.g. \(\overrightarrow {{\rm{OA}}} + \overrightarrow {{\rm{AB}}} = \overrightarrow {{\rm{OB}}} \) , \(\overrightarrow {{\rm{AB}}} = \left( {\begin{array}{*{20}{c}}
{ – 8}\\
{ – 5}\\
{25}
\end{array}} \right) – \left( {\begin{array}{*{20}{c}}
{ – 9}\\
{ – 4}\\
{ – 1}
\end{array}} \right)\)
\(\overrightarrow {{\rm{AB}}} = \left( {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
{26}
\end{array}} \right)\) A1 N2
(ii) finding \(\overrightarrow {{\rm{AC}}} = \left( {\begin{array}{*{20}{c}}
7\\
2\\
2
\end{array}} \right)\) A1
evidence of finding magnitude (M1)
e.g. \(|\overrightarrow {{\rm{AC}}} | = \sqrt {{7^2} + {2^2} + {2^2}} \)
\(|\overrightarrow {{\rm{AC}}} | = \sqrt {57} \) A1 N3
[5 marks]
Question
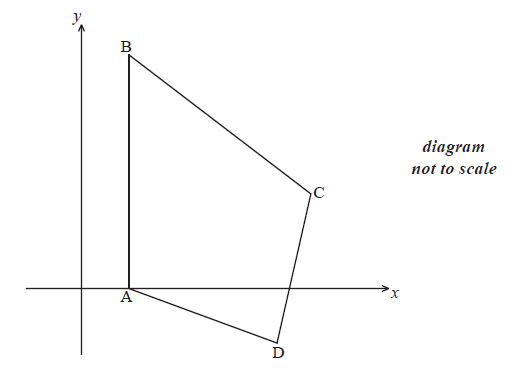
The diagram shows quadrilateral ABCD with vertices A(1, 0), B(1, 5), C(5, 2) and D(4, −1) .
(i) Show that \(\overrightarrow {{\rm{AC}}} = \left( {\begin{array}{*{20}{c}}
4\\
2
\end{array}} \right)\) .
(ii) Find \(\overrightarrow {{\rm{BD}}} \) .
(iii) Show that \(\overrightarrow {{\rm{AC}}} \) is perpendicular to \(\overrightarrow {{\rm{BD}}} \) .
The line (AC) has equation \({\boldsymbol{r}} = {\boldsymbol{u}} + s{\boldsymbol{v}}\) .
(i) Write down vector u and vector v .
(ii) Find a vector equation for the line (BD).
The lines (AC) and (BD) intersect at the point \({\text{P}}(3{\text{, }}k)\) .
Show that \(k = 1\) .
The lines (AC) and (BD) intersect at the point \({\text{P}}(3{\text{, }}k)\) .
Hence find the area of triangle ACD.
Answer/Explanation
Markscheme
(i) correct approach A1
e.g. \(\overrightarrow {{\rm{OC}}} – \overrightarrow {{\rm{OA}}} \) , \(\left( {\begin{array}{*{20}{c}}
5\\
2
\end{array}} \right) – \left( {\begin{array}{*{20}{c}}
1\\
0
\end{array}} \right)\)
\(\overrightarrow {{\rm{AC}}} = \left( {\begin{array}{*{20}{c}}
4\\
2
\end{array}} \right)\) AG N0
(ii) appropriate approach (M1)
e.g. \({\mathop{\rm D}\nolimits} – {\rm{B}}\) , \(\left( {\begin{array}{*{20}{c}}
4\\
{ – 1}
\end{array}} \right) – \left( {\begin{array}{*{20}{c}}
1\\
5
\end{array}} \right)\) , move 3 to the right and 6 down
\(\overrightarrow {{\rm{BD}}} = \left( {\begin{array}{*{20}{c}}
3\\
{ – 6}
\end{array}} \right)\) A1 N2
(iii) finding the scalar product A1
e.g. \(4(3) + 2( – 6)\) , \(12 – 12\)
valid reasoning R1
e.g. \(4(3) + 2( – 6) = 0\) , scalar product is zero
\(\overrightarrow {{\rm{AC}}} \) is perpendicular to \(\overrightarrow {{\rm{BD}}} \) AG N0
[5 marks]
(i) correct “position” vector for u; “direction” vector for v A1A1 N2
e.g. \({\boldsymbol{u}} = \left( {\begin{array}{*{20}{c}}
5\\
2
\end{array}} \right)\) , \({\boldsymbol{u}} = \left( {\begin{array}{*{20}{c}}
1\\
0
\end{array}} \right)\) ; \({\boldsymbol{v}} = \left( {\begin{array}{*{20}{c}}
4\\
2
\end{array}} \right)\) , \({\boldsymbol{v}} = \left( {\begin{array}{*{20}{c}}
{ – 2}\\
{ – 1}
\end{array}} \right)\)
accept in equation e.g. \(\left( {\begin{array}{*{20}{c}}
5\\
2
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
{ – 4}\\
{ – 2}
\end{array}} \right)\)
(ii) any correct equation in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) , where \({\boldsymbol{b}} = \overrightarrow {{\rm{BD}}} \)
\({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
1\\
5
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
3\\
{ – 6}
\end{array}} \right)\) , \(\left( {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
4\\
{ – 1}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
{ – 1}\\
2
\end{array}} \right)\) A2 N2
[4 marks]
METHOD 1
substitute (3, k) into equation for (AC) or (BD) (M1)
e.g. \(3 = 1 + 4s\) , \(3 = 1 + 3t\)
value of t or s A1
e.g. \(s = \frac{1}{2}\) , \( – \frac{1}{2}\) , \(t = \frac{2}{3}\) , \( – \frac{1}{3}\)
substituting A1
e.g. \(k = 0 + \frac{1}{2}(2)\)
\(k = 1\) AG N0
METHOD 2
setting up two equations (M1)
e.g. \(1 + 4s = 4 + 3t\) , \(2s = – 1 – 6t\) ; setting vector equations of lines equal
value of t or s A1
e.g. \(s = \frac{1}{2}\) , \( – \frac{1}{2}\) , \(t = \frac{2}{3}\) , \( – \frac{1}{3}\)
substituting A1
e.g. \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
4\\
{ – 1}
\end{array}} \right) – \frac{1}{3}\left( {\begin{array}{*{20}{c}}
3\\
{ – 6}
\end{array}} \right)\)
\(k = 1\) AG N0
[3 marks]
\(\overrightarrow {{\rm{PD}}} = \left( {\begin{array}{*{20}{c}}
1\\
{ – 2}
\end{array}} \right)\) (A1)
\(|\overrightarrow {{\rm{PD}}} | = \sqrt {{2^2} + {1^2}} \) \(( = \sqrt 5 )\) (A1)
\(|\overrightarrow {{\rm{AC}}} | = \sqrt {{4^2} + {2^2}} \) \(( = \sqrt {20} )\) (A1)
area \( = \frac{1}{2} \times |\overrightarrow {{\rm{AC}}} | \times |\overrightarrow {{\rm{PD}}} |\) (\( = \frac{1}{2} \times \sqrt {20} \times \sqrt 5 \)) M1
\( = 5\) A1 N4
[5 marks]
Question
A line L passes through \({\text{A}}(1{\text{, }} – 1{\text{, }}2)\) and is parallel to the line \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{ – 2}\\
1\\
5
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
1\\
3\\
{ – 2}
\end{array}} \right)\) .
The line L passes through point P when \(t = 2\) .
Write down a vector equation for L in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) .
Find
(i) \(\overrightarrow {{\rm{OP}}} \) ;
(ii) \(|\overrightarrow {{\rm{OP}}} |\) .
Answer/Explanation
Markscheme
correct equation in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) A2 N2
\({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
2
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
3\\
{ – 2}
\end{array}} \right)\)
[2 marks]
(i) attempt to substitute \(t = 2\) into the equation (M1)
e.g. \(\left( {\begin{array}{*{20}{c}}
2\\
6\\
{ – 4}
\end{array}} \right)\) , \(\left( {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
2
\end{array}} \right) + 2\left( {\begin{array}{*{20}{c}}
1\\
3\\
{ – 2}
\end{array}} \right)\)
\(\overrightarrow {{\rm{OP}}} = \left( {\begin{array}{*{20}{c}}
3\\
5\\
{ – 2}
\end{array}} \right)\) A1 N2
(ii) correct substitution into formula for magnitude A1
e.g. \(\sqrt {{3^2} + {5^2} + – {2^2}} \) , \(\sqrt {{3^2} + {5^2} + {2^2}} \)
\(|\overrightarrow {{\rm{OP}}}| = \sqrt {38} \) A1 N1
[4 marks]
Question
The line \({L_1}\) passes through the points P(2, 4, 8) and Q(4, 5, 4) .
The line \({L_2}\) is perpendicular to \({L_1}\) , and parallel to \(\left( {\begin{array}{*{20}{c}}
{3p}\\
{2p}\\
4
\end{array}} \right)\) , where \(p \in \mathbb{Z}\) .
(i) Find \(\overrightarrow {{\rm{PQ}}} \) .
(ii) Hence write down a vector equation for \({L_1}\) in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + s{\boldsymbol{b}}\) .
(i) Find the value of p .
(ii) Given that \({L_2}\) passes through \({\text{R}}(10{\text{, }}6{\text{, }}- 40)\) , write down a vector equation for \({L_2}\) .
The lines \({L_1}\) and \({L_2}\) intersect at the point A. Find the x-coordinate of A.
Answer/Explanation
Markscheme
(i) evidence of approach (M1)
e.g. \(\overrightarrow {{\rm{PO}}} + \overrightarrow {{\rm{OQ}}} \) , \({\rm{P}} – {\rm{Q}}\)
\(\overrightarrow {{\rm{PQ}}} = \left( {\begin{array}{*{20}{c}}
2\\
1\\
{ – 4}
\end{array}} \right)\) A1 N2
(ii) any correct equation in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + s{\boldsymbol{b}}\) (accept any parameter for s)
where a is \(\left( {\begin{array}{*{20}{c}}
2\\
4\\
8
\end{array}} \right)\) or \(\left( {\begin{array}{*{20}{c}}
4\\
5\\
4
\end{array}} \right)\) , and b is a scalar multiple of \(\left( {\begin{array}{*{20}{c}}
2\\
1\\
{ – 4}
\end{array}} \right)\) A2 N2
e.g. \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
2\\
4\\
8
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
2\\
1\\
{ – 4}
\end{array}} \right)\) , \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{4 + 2s}\\
{5 + 1s}\\
{4 – 4s}
\end{array}} \right)\) , \({\boldsymbol{r}} = 2{\boldsymbol{i}} + 4{\boldsymbol{j}} + 8{\boldsymbol{k}} + s(2{\boldsymbol{i}} + 1{\boldsymbol{j}} – 4{\boldsymbol{k}})\)
Note: Award A1 for the form \({\boldsymbol{a}} + s{\boldsymbol{b}}\) , A1 for \({\boldsymbol{L}} = {\boldsymbol{a}} + s{\boldsymbol{b}}\) , A0 for \({\boldsymbol{r}} = {\boldsymbol{b}} + s{\boldsymbol{a}}\) .
[4 marks]
(i) choosing correct direction vectors for \({L_1}\) and \({L_2}\) (A1) (A1)
e.g. \(\left( {\begin{array}{*{20}{c}}
2\\
1\\
{ – 4}
\end{array}} \right)\) , \(\left( {\begin{array}{*{20}{c}}
{3p}\\
{2p}\\
4
\end{array}} \right)\)
evidence of equating scalar product to 0 (M1)
correct calculation of scalar product A1
e.g. \(2 \times 3p + 1 \times 2p + ( – 4) \times 4\) , \(8p – 16 = 0\)
\(p = 2\) A1 N3
(ii) any correct expression in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) (accept any parameter for t)
where a is \(\left( {\begin{array}{*{20}{c}}
{10}\\
6\\
{ – 40}
\end{array}} \right)\) , and b is a scalar multiple of \(\left( {\begin{array}{*{20}{c}}
6\\
4\\
4
\end{array}} \right)\) A2 N2
e.g. \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{10}\\
6\\
{ – 40}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
6\\
4\\
4
\end{array}} \right)\) , \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{10 + 6s}\\
{6 + 4s}\\
{ – 40 + 4s}
\end{array}} \right)\) , \({\boldsymbol{r}} = 10{\boldsymbol{i}} + 6{\boldsymbol{j}} – 40{\boldsymbol{k}} + s(6{\boldsymbol{i}} + 4{\boldsymbol{j}} + 4{\boldsymbol{k}})\)
Note: Award A1 for the form \({\boldsymbol{a}} + t{\boldsymbol{b}}\) , A1 for \({\boldsymbol{L}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) (unless they have been penalised for \({\boldsymbol{L}} = {\boldsymbol{a}} + s{\boldsymbol{b}}\) in part (a)), A0 for \({\boldsymbol{r}} = {\boldsymbol{b}} + t{\boldsymbol{a}}\) .
[7 marks]
appropriate approach (M1)
e.g. \(\left( {\begin{array}{*{20}{c}}
2\\
4\\
8
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
2\\
1\\
{ – 4}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{10}\\
6\\
{ – 40}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
6\\
4\\
4
\end{array}} \right)\)
any two correct equations with different parameters A1A1
e.g. \(2 + 2s = 10 + 6t\) , \(4 + s = 6 + 4t\) , \(8 – 4s = – 40 + 4t\)
attempt to solve simultaneous equations (M1)
correct working (A1)
e.g. \( – 6 = – 2 – 2t\) , \(4 = 2t\) , \( – 4 + 5s = 46\) , \(5s = 50\)
one correct parameter \(s = 10\) , \(t = 2\) A1
\(x = 22\) (accept (22, 14, −32)) A1 N4
[7 marks]
Question
A line \({L_1}\) passes though points P(−1, 6, −1) and Q(0, 4, 1) .
A second line \({L_2}\) has equation \(r = \left( {\begin{array}{*{20}{c}}
4\\
2\\
{ – 1}
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
3\\
0\\
{ – 4}
\end{array}} \right)\) .
(i) Show that \(\overrightarrow {{\rm{PQ}}} = \left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
2
\end{array}} \right)\) .
(ii) Hence, write down an equation for \({L_1}\) in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) .
Find the cosine of the angle between \(\overrightarrow {{\rm{PQ}}} \) and \({L_2}\) .
The lines \({L_1}\) and \({L_2}\) intersect at the point R. Find the coordinates of R.
Answer/Explanation
Markscheme
(i) evidence of correct approach A1
e.g. \(\overrightarrow {{\rm{PQ}}} = \overrightarrow {{\rm{OQ}}} – \overrightarrow {{\rm{OP}}} \) , \(Q – P\)
\(\overrightarrow {{\rm{PQ}}} = \left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
2
\end{array}} \right)\) AG N0
(ii) any correct equation in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) A2 N2
where a is either \(\overrightarrow {{\rm{OP}}} \) or \(\overrightarrow {{\rm{OQ}}} \) and b is a scalar multiple of \(\overrightarrow {{\rm{PQ}}} \)
e.g. \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{ – 1}\\
6\\
{ – 1}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
2
\end{array}} \right)\) , \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
t \\
{4 – 2t} \\
{1 + 2t}
\end{array}} \right)\), \({\boldsymbol{r}} = 4{\boldsymbol{j}} + {\boldsymbol{k}} + t({\boldsymbol{i}} – 2{\boldsymbol{j}} + 2{\boldsymbol{k}})\)
[3 marks]
choosing a correct direction vector for \({L_2}\) (A1)
e.g. \(\left( {\begin{array}{*{20}{c}}
3\\
0\\
{ – 4}
\end{array}} \right)\)
finding scalar products and magnitudes (A1)(A1)(A1)
scalar product \( = 1(3) – 2(0) + 2( – 4)\) \(( = – 5)\)
magnitudes \( = \sqrt {{1^2} + {{( – 2)}^2} + {2^2}} \) \(( = 3)\) , \(\sqrt {{3^2} + {0^2} + {{( – 4)}^2}} \) \(( = 5)\)
substitution into formula M1
e.g. \(\cos \theta = \frac{{ – 5}}{{\sqrt 9 \times \sqrt {25} }}\)
\(\cos \theta = – \frac{1}{3}\) A2 N5
[7 marks]
evidence of valid approach (M1)
e.g. equating lines, \({L_1} = {L_2}\)
EITHER
one correct equation in one variable A2
e.g. \(6 – 2t = 2\)
OR
two correct equations in two variables A1A1
e.g. \(2t + 4s = 0\) , \(t – 3s = 5\)
THEN
attempt to solve (M1)
one correct parameter A1
e.g. \(t = 2\) , \(s = – 1\)
correct substitution of either parameter (A1)
e.g. \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
4\\
2\\
{ – 1}
\end{array}} \right) + ( – 1)\left( {\begin{array}{*{20}{c}}
3\\
0\\
{ – 4}
\end{array}} \right)\) , \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{ – 1}\\
6\\
{ – 1}
\end{array}} \right) + ( + 2)\left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
2
\end{array}} \right)\)
coordinates \({\text{R}}(1{\text{, }}2{\text{, }}3)\) A1 N3
[7 marks]
Question
The line L passes through the point \((5, – 4,10)\) and is parallel to the vector \(\left( {\begin{array}{*{20}{c}}
4\\
{ – 2}\\
5
\end{array}} \right)\) .
Write down a vector equation for line L .
The line L intersects the x-axis at the point P. Find the x-coordinate of P.
Answer/Explanation
Markscheme
any correct equation in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) (accept any parameter for t)
where a is \(\left( {\begin{array}{*{20}{c}}
5\\
{ – 4}\\
{10}
\end{array}} \right)\) , and b is a scalar multiple of \(\left( {\begin{array}{*{20}{c}}
4\\
{ – 2}\\
5
\end{array}} \right)\) A2 N2
e.g. \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
5 \\
{ – 4} \\
{10}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
4 \\
{ – 2} \\
5
\end{array}} \right){\text{, }}{\boldsymbol{r}} = 5{\boldsymbol{i}} – 4{\boldsymbol{j}} + 10{\boldsymbol{k}} + t( – 8{\boldsymbol{i}} + 4{\boldsymbol{j}} – 10{\boldsymbol{k}})\)
Note: Award A1 for the form \({\boldsymbol{a}} + t{\boldsymbol{b}}\) , A1 for \(L = {\boldsymbol{a}} + t{\boldsymbol{b}}\) , A0 for \({\boldsymbol{r}} = {\boldsymbol{b}} + t{\boldsymbol{a}}\) .
[2 marks]
recognizing that \(y = 0\) or \(z = 0\) at x-intercept (seen anywhere) (R1)
attempt to set up equation for x-intercept (must suggest \(x \ne 0\) ) (M1)
e.g. \(L = \left( {\begin{array}{*{20}{c}}
x\\
0\\
0
\end{array}} \right)\) , \(5 + 4t = x\) , \(r = \left( {\begin{array}{*{20}{c}}
1\\
0\\
0
\end{array}} \right)\)
one correct equation in one variable (A1)
e.g. \( – 4 – 2t = 0\) , \(10 + 5t = 0\)
finding \(t = – 2\) A1
correct working (A1)
e.g. \(x = 5 + ( – 2)(4)\)
\(x = – 3\) (accept \(( – 3{\text{, }}0{\text{, }}0)\)) A1 N3
[6 marks]
Question
Consider points A(\(1\), \( – 2\), \( -1\)) , B(\(7\), \( – 4\), \(3\)) and C(\(1\), \( -2\), \(3\)) . The line \({L_1}\) passes through C and is parallel to \(\overrightarrow {{\rm{AB}}} \) .
A second line, \({L_2}\) , is given by \(\boldsymbol{r} = \left( {\begin{array}{*{20}{c}}
{ – 1}\\
2\\
{15}
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
3\\
{ – 3}\\
p
\end{array}} \right)\) .
Find \(\overrightarrow {{\rm{AB}}} \) .
Hence, write down a vector equation for \({L_1}\) .
Given that \({L_1}\) is perpendicular to \({L_2}\) , show that \(p = – 6\) .
The line \({L_1}\) intersects the line \({L_2}\) at point Q. Find the \(x\)-coordinate of Q.
Answer/Explanation
Markscheme
valid approach (M1)
eg \(\left( {\begin{array}{*{20}{c}}
7\\
{ – 4}\\
3
\end{array}} \right) – \left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
{ – 1}
\end{array}} \right)\) , \({\rm{A}} – {\rm{B}}\) , \(\overrightarrow {{\rm{AB}}} = \overrightarrow {{\rm{AO}}} + \overrightarrow {{\rm{OB}}} \)
\(\overrightarrow {{\rm{AB}}} = \left( {\begin{array}{*{20}{c}}
6\\
{ – 2}\\
4
\end{array}} \right)\) A1 N2
[2 marks]
any correct equation in the form \(\boldsymbol{r} = \boldsymbol{a} + t\boldsymbol{b}\) (accept any parameter for \(t\))
where \(\boldsymbol{a} = \left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
3
\end{array}} \right)\) and \(\boldsymbol{b}\) is a scalar multiple of \(\overrightarrow {{\rm{AB}}} \) A2 N2
eg \(\boldsymbol{r} = \left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
3
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
6\\
{ – 2}\\
4
\end{array}} \right)\) , \((x,y,z) = (1, – 2,3) + t(3, – 1,2)\) , \(\boldsymbol{r} = \left( {\begin{array}{*{20}{c}}
{1 + 6t}\\
{ – 2 – 2t}\\
{3 + 4t}
\end{array}} \right)\)
Note: Award A1 for \(\boldsymbol{a} + t\boldsymbol{b}\) , A1 for \({L_1} = \boldsymbol{a} + t\boldsymbol{b}\) , A0 for \(\boldsymbol{r} = \boldsymbol{b} + t\boldsymbol{a}\) .
[2 marks]
recognizing that scalar product \( = 0\) (seen anywhere) R1
correct calculation of scalar product (A1)
eg \(6(3) – 2( – 3) + 4p\) , \(18 + 6 + 4p\)
correct working A1
eg \(24 + 4p = 0\) , \(4p = – 24\)
\(p = – 6\) AG N0
[3 marks]
setting lines equal (M1)
eg \({L_1} = {L_2}\) , \(\left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
3
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
6\\
{ – 2}\\
4
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 1}\\
2\\
{15}
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
3\\
{ – 3}\\
{ – 6}
\end{array}} \right)\)
any two correct equations with different parameters A1A1
eg \(1 + 6t = 1 + 3s\) , \( – 2 – 2t = 2 – 3s\) , \(3 + 4t = 15 – 6s\)
attempt to solve their simultaneous equations (M1)
one correct parameter A1
eg \(t = \frac{1}{2}\) , \(s = \frac{5}{3}\)
attempt to substitute parameter into vector equation (M1)
eg \(\left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
3
\end{array}} \right) + \frac{1}{2}\left( {\begin{array}{*{20}{c}}
6\\
{ – 2}\\
4
\end{array}} \right)\) , \(1 + \frac{1}{2} \times 6\)
\(x = 4\) (accept (4, -3, 5), ignore incorrect values for \(y\) and \(z\)) A1 N3
[7 marks]
Question
The line \({L_1}\) passes through the points \(\rm{A}(2, 1, 4)\) and \(\rm{B}(1, 1, 5)\).
Another line \({L_2}\) has equation r = \(\left( \begin{array}{c}4\\7\\ – 4\end{array} \right) + s\left( \begin{array}{c}0\\ – 1\\1\end{array} \right)\) . The lines \({L_1}\) and \({L_2}\) intersect at the point P.
Show that \(\overrightarrow {{\text{AB}}} = \) \(\left( \begin{array}{c} – 1\\0\\1\end{array} \right)\)
Hence, write down a direction vector for \({L_1}\);
Hence, write down a vector equation for \({L_1}\).
Find the coordinates of P.
Write down a direction vector for \({L_2}\).
Hence, find the angle between \({L_1}\) and \({L_2}\).
Answer/Explanation
Markscheme
correct approach A1
eg \(\left( \begin{array}{c}1\\1\\5\end{array} \right) – \left( \begin{array}{l}2\\1\\4\end{array} \right)\), \({\text{AO}} + {\text{OB}}\), \(b – a\)
\(\overrightarrow {{\text{AB}}} = \) \(\left( \begin{array}{c} – 1\\0\\1\end{array} \right)\) AG N0
[1 mark]
correct vector (or any multiple) A1 N1
eg d = \(\left( \begin{array}{c} – 1\\0\\1\end{array} \right)\)
[1 mark]
any correct equation in the form r = a + tb (accept any parameter for t)
where a is \(\left( \begin{array}{c}2\\1\\4\end{array} \right)\) or \(\left( \begin{array}{c}1\\1\\5\end{array} \right)\) , and b is a scalar multiple of \(\left( \begin{array}{c} – 1\\0\\1\end{array} \right)\) A2 N2
eg r = \(\left( \begin{array}{c}1\\1\\5\end{array} \right) + t\left( \begin{array}{c} – 1\\0\\1\end{array} \right),\left( \begin{array}{c}x\\y\\z\end{array} \right) = \left( \begin{array}{c}2 – s\\1\\4 + s\end{array} \right)\)
Note: Award A1 for a + tb, A1 for \({L_1}\) = a + tb, A0 for r = b + ta.
[2 marks]
valid approach (M1)
eg \({r_1} = {r_2}\), \(\left( \begin{array}{c}2\\1\\4\end{array} \right) + t\left( \begin{array}{c} – 1\\0\\1\end{array} \right) = \left( \begin{array}{c}4\\7\\ – 4\end{array} \right) + s\left( \begin{array}{c}0\\ – 1\\1\end{array} \right)\)
one correct equation in one parameter A1
eg \(2 – t = 4, 1 = 7 – s, 1 – t = 4\)
attempt to solve (M1)
eg \(2 – 4 = t, s = 7 – 1, t = 1 – 4\)
one correct parameter A1
eg \(t = -2, s = 6, t = -3\),
attempt to substitute their parameter into vector equation (M1)
eg \(\left( \begin{array}{c}4\\7\\ – 4\end{array} \right) + 6\left( \begin{array}{c}0\\ – 1\\1\end{array} \right)\)
P(4, 1, 2) (accept position vector) A1 N2
[6 marks]
correct direction vector for \({L_2}\) A1 N1
eg \(\left( \begin{array}{c}0\\-1\\ 1\end{array} \right)\), \(\left( \begin{array}{c}0\\2\\ – 2\end{array} \right)\)
[1 mark]
correct scalar product and magnitudes for their direction vectors (A1)(A1)(A1)
scalar product \( = 0 \times – 1 + – 1 \times 0 + 1 \times 1{\text{ }}( = 1)\)
magnitudes \( = \sqrt {{0^2} + {{( – 1)}^2} + {1^2}} ,{\text{ }}\sqrt { – {1^2} + {0^2} + {1^2}} \left( {\sqrt 2 ,{\text{ }}\sqrt 2 } \right)\)
attempt to substitute their values into formula M1
eg \(\frac{{0 + 0 + 1}}{{\left( {\sqrt {{0^2} + {{( – 1)}^2} + {1^2}} } \right) \times \left( {\sqrt { – {1^2} + {0^2} + {1^2}} } \right)}},{\text{ }}\frac{1}{{\sqrt 2 \times \sqrt 2 }}\)
correct value for cosine, \(\frac{1}{2}\) A1
angle is \(\frac{\pi }{3}{\text{ }}( = {60^ \circ })\) A1 N1
[6 marks]
Question
The line \(L\) is parallel to the vector \(\left( \begin{array}{l}3\\2\end{array} \right)\).
The line \(L\) passes through the point \((9, 4)\).
Find the gradient of the line \(L\).
Find the equation of the line \(L\) in the form \(y = ax + b\).
Write down a vector equation for the line \(L\).
Answer/Explanation
Markscheme
attempt to find gradient (M1)
eg reference to change in \(x\) is \(3\) and/or \(y\) is \(2\), \(\frac{3}{2}\)
gradient \( = \frac{2}{3}\) A1 N2
[2 marks]
attempt to substitute coordinates and/or gradient into Cartesian equation
for a line (M1)
eg \(y – 4 = m(x – 9),{\text{ }}y = \frac{2}{3}x + b,{\text{ }}9 = a(4) + c\)
correct substitution (A1)
eg \(4 = \frac{2}{3}(9) + c,{\text{ }}y – 4 = \frac{2}{3}(x – 9)\)
\(y = \frac{2}{3}x – 2{\text{ }}\left( {{\text{accept }}a = \frac{2}{3},{\text{ }}b = – 2} \right)\) A1 N2
[3 marks]
any correct equation in the form r = a + tb (any parameter for t), where a indicates position eg \(\left( \begin{array}{l}9\\4\end{array} \right)\) or \(\left( \begin{array}{c}0\\ – 2\end{array} \right)\), and b is a scalar multiple of \(\left( \begin{array}{l}3\\2\end{array} \right)\)
eg r = \(\left( \begin{array}{c}9\\4\end{array} \right) + t\left( \begin{array}{c}3\\2\end{array} \right),\left( \begin{array}{c}x\\y\end{array} \right) = \left( \begin{array}{c}3t + 9\\2t + 4\end{array} \right)\), r = 0i − 2 j + s(3i + 2 j) A2 N2
Note: Award A1 for a + tb, A1 for L = a + tb, A0 for r = b + ta.
[2 marks]
Question
Distances in this question are in metres.
Ryan and Jack have model airplanes, which take off from level ground. Jack’s airplane takes off after Ryan’s.
The position of Ryan’s airplane \(t\) seconds after it takes off is given by \(\boldsymbol{r}=\left( \begin{array}{c}5\\6\\0\end{array} \right) + t\left( \begin{array}{c} – 4\\2\\4\end{array} \right)\).
Find the speed of Ryan’s airplane.
Find the height of Ryan’s airplane after two seconds.
The position of Jack’s airplane \(s\) seconds after it takes off is given by r = \(\left( \begin{array}{c} – 39\\44\\0\end{array} \right) + s\left( \begin{array}{c}4\\ – 6\\7\end{array} \right)\).
Show that the paths of the airplanes are perpendicular.
The two airplanes collide at the point \((-23, 20, 28)\).
How long after Ryan’s airplane takes off does Jack’s airplane take off?
Answer/Explanation
Markscheme
valid approach (M1)
eg magnitude of direction vector
correct working (A1)
eg \(\sqrt {{{( – 4)}^2} + {2^2} + {4^2}} ,{\text{ }}\sqrt { – {4^2} + {2^2} + {4^2}} \)
\(6{\text{ (m}}{{\text{s}}^{ – 1}})\) A1 N2
[3 marks]
substituting \(2\) for \(t\) (A1)
eg \(0 + 2(4)\), r = \(\left( \begin{array}{c}5\\6\\0\end{array} \right) + 2\left( \begin{array}{c} – 4\\2\\4\end{array} \right),\left( \begin{array}{c} – 3\\10\\8\end{array} \right)\), \(y = 10\)
\(8\) (metres) A1 N2
[2 marks]
METHOD 1
choosing correct direction vectors \(\left( \begin{array}{c} – 4\\2\\4\end{array} \right)\) and \(\left( \begin{array}{c}4\\ – 6\\7\end{array} \right)\) (A1)(A1)
evidence of scalar product M1
eg a \( \cdot \) b
correct substitution into scalar product (A1)
eg \(( – 4 \times 4) + (2 \times – 6) + (4 \times 7)\)
evidence of correct calculation of the scalar product as \(0\) A1
eg \( – 16 – 12 + 28 = 0\)
directions are perpendicular AG N0
METHOD 2
choosing correct direction vectors \(\left( \begin{array}{c} – 4\\2\\4\end{array} \right)\) and \(\left( \begin{array}{c}4\\ – 6\\7\end{array} \right)\) (A1)(A1)
attempt to find angle between vectors M1
correct substitution into numerator A1
eg \(\cos \theta = \frac{{ – 16 – 12 + 28}}{{\left| a \right|\left| b \right|}},{\text{ }}\cos \theta = 0\)
\(\theta = 90^\circ \) A1
directions are perpendicular AG N0
[5 marks]
METHOD 1
one correct equation for Ryan’s airplane (A1)
eg \(5 – 4t = – 23,{\text{ }}6 + 2t = 20,{\text{ }}0 + 4t = 28\)
\(t = 7\) A1
one correct equation for Jack’s airplane (A1)
eg \( – 39 + 4s = – 23,{\text{ }}44 – 6s = 20,{\text{ }}0 + 7s = 28\)
\(s = 4\) A1
\(3\) (seconds later) A1 N2
METHOD 2
valid approach (M1)
eg \(\left( \begin{array}{c}5\\6\\0\end{array} \right) + t\left( \begin{array}{c} – 4\\2\\4\end{array} \right) = \left( \begin{array}{c} – 39\\44\\0\end{array} \right) + s\left( \begin{array}{c}4\\ – 6\\7\end{array} \right)\), one correct equation
two correct equations (A1)
eg \(5 – 4t = – 39 + 4s,{\text{ }}6 + 2t = 44 – 6s,{\text{ }}4t = 7s\)
\(t = 7\) A1
\(s = 4\) A1
\(3\) (seconds later) A1 N2
[5 marks]
Question
Let \({L_x}\) be a family of lines with equation given by \(r\) \( = \left( {\begin{array}{*{20}{c}} x \\ {\frac{2}{x}} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} {{x^2}} \\ { – 2} \end{array}} \right)\), where \(x > 0\).
Write down the equation of \({L_1}\).
A line \({L_a}\) crosses the \(y\)-axis at a point \(P\).
Show that \(P\) has coordinates \(\left( {0,{\text{ }}\frac{4}{a}} \right)\).
The line \({L_a}\) crosses the \(x\)-axis at \({\text{Q}}(2a,{\text{ }}0)\). Let \(d = {\text{P}}{{\text{Q}}^2}\).
Show that \(d = 4{a^2} + \frac{{16}}{{{a^2}}}\).
There is a minimum value for \(d\). Find the value of \(a\) that gives this minimum value.
Answer/Explanation
Markscheme
attempt to substitute \(x = 1\) (M1)
eg\(\;\;\;\)r \( = \left( {\begin{array}{*{20}{c}} 1 \\ {\frac{2}{1}} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} {{1^2}} \\ { – 2} \end{array}} \right),{\text{ }}{L_1} = \left( {\begin{array}{*{20}{c}} 1 \\ 2 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 1 \\ { – 2} \end{array}} \right)\)
correct equation (vector or Cartesian, but do not accept “\({L_1}\)”)
eg\(\;\;\;\)r \( = \left( {\begin{array}{*{20}{c}} 1 \\ 2 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 1 \\ { – 2} \end{array}} \right),{\text{ }}y = – 2x + 4\;\;\;\)(must be an equation) A1 N2
[2 marks]
appropriate approach (M1)
eg\(\;\;\;\left( {\begin{array}{*{20}{c}} 0 \\ y \end{array}} \right) = \left( {\begin{array}{*{20}{c}} a \\ {\frac{2}{a}} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} {{a^2}} \\ { – 2} \end{array}} \right)\)
correct equation for \(x\)-coordinate A1
eg\(\;\;\;0 = a + t{a^2}\)
\(t = \frac{{ – 1}}{a}\) A1
substituting their parameter to find \(y\) (M1)
eg\(\;\;\;y = \frac{2}{a} – 2\left( {\frac{{ – 1}}{a}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} a \\ {\frac{2}{a}} \end{array}} \right) – \frac{1}{a}\left( {\begin{array}{*{20}{c}} {{a^2}} \\ { – 2} \end{array}} \right)\)
correct working A1
eg\(\;\;\;y = \frac{2}{a} + \frac{2}{a},{\text{ }}\left( {\begin{array}{*{20}{c}} a \\ {\frac{2}{a}} \end{array}} \right) – \left( {\begin{array}{*{20}{c}} a \\ { – \frac{2}{a}} \end{array}} \right)\)
finding correct expression for \(y\) A1
eg\(\;\;\;y = \frac{4}{a},{\text{ }}\left( {\begin{array}{*{20}{c}} 0 \\ {\frac{4}{a}} \end{array}} \right)\) \({\text{P}}\left( {0,{\text{ }}\frac{4}{a}} \right)\) AG N0
[6 marks]
valid approach M1
eg\(\;\;\;\)distance formula, Pythagorean Theorem, \(\overrightarrow {{\text{PQ}}} = \left( {\begin{array}{*{20}{c}} {2a} \\ { – \frac{4}{a}} \end{array}} \right)\)
correct simplification A1
eg\(\;\;\;{(2a)^2} + {\left( {\frac{4}{a}} \right)^2}\)
\(d = 4{a^2} + \frac{{16}}{{{a^2}}}\) AG N0
[2 marks]
recognizing need to find derivative (M1)
eg\(\;\;\;d’,{\text{ }}d'(a)\)
correct derivative A2
eg\(\;\;\;8a – \frac{{32}}{{{a^3}}},{\text{ }}8x – \frac{{32}}{{{x^3}}}\)
setting their derivative equal to \(0\) (M1)
eg\(\;\;\;8a – \frac{{32}}{{{a^3}}} = 0\)
correct working (A1)
eg\(\;\;\;8a = \frac{{32}}{{{a^3}}},{\text{ }}8{a^4} – 32 = 0\)
working towards solution (A1)
eg\(\;\;\;{a^4} = 4,{\text{ }}{a^2} = 2,{\text{ }}a = \pm \sqrt 2 \)
\(a = \sqrt[4]{4}\;\;\;(a = \sqrt 2 )\;\;\;({\text{do not accept }} \pm \sqrt 2 )\) A1 N3
[7 marks]
Total [17 marks]
Question
A line \(L\) passes through points \({\text{A}}( – 2,{\text{ }}4,{\text{ }}3)\) and \({\text{B}}( – 1,{\text{ }}3,{\text{ }}1)\).
(i) Show that \(\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 1 \\ { – 1} \\ { – 2} \end{array}} \right)\).
(ii) Find \(\left| {\overrightarrow {{\text{AB}}} } \right|\).
Find a vector equation for \(L\).
The following diagram shows the line \(L\) and the origin \(O\). The point \(C\) also lies on \(L\).
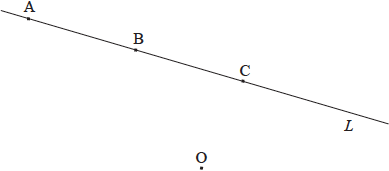
Point \(C\) has position vector \(\left( {\begin{array}{*{20}{c}} 0 \\ y \\ { – 1} \end{array}} \right)\).
Show that \(y = 2\).
(i) Find \(\overrightarrow {{\text{OC}}} \bullet \overrightarrow {{\text{AB}}} \).
(ii) Hence, write down the size of the angle between \(C\) and \(L\).
Hence or otherwise, find the area of triangle \(OAB\).
Answer/Explanation
Markscheme
(i) correct approach A1
eg\(\;\;\;{\text{B}} – {\text{A, AO}} + {\text{OB}}\)
\(\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 1 \\ { – 1} \\ { – 2} \end{array}} \right)\) AG N0
(ii) correct substitution (A1)
eg\(\;\;\;\sqrt {{{(1)}^2} + {{( – 1)}^2} + {{( – 2)}^2}} ,{\text{ }}\sqrt {1 + 1 + 4} \)
\(\left| {\overrightarrow {{\text{AB}}} } \right| = \sqrt 6 \) A1 N2
[3 marks]
any correct equation in the form \(r = a + tb\) (any parameter for \(t\))
where \(a\) is \(\left( {\begin{array}{*{20}{c}} { – 2} \\ 4 \\ 3 \end{array}} \right)\) or \(\left( {\begin{array}{*{20}{c}} { – 1} \\ 3 \\ 1 \end{array}} \right)\) and \(b\) is a scalar multiple of \(\left( {\begin{array}{*{20}{c}} 1 \\ { – 1} \\ { – 2} \end{array}} \right)\) A2 N2
eg\(\;\;\;\(r\) = \left( {\begin{array}{*{20}{c}} { – 2} \\ 4 \\ 3 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 1 \\ { – 1} \\ { – 2} \end{array}} \right),{\text{ }}(x,{\text{ }}y,{\text{ }}z) = ( – 1,{\text{ }}3,{\text{ }}1) + t(1,{\text{ }} – 1,{\text{ }} – 2),{\text{ }}{\mathbf{r}} = \left( {\begin{array}{*{20}{c}} { – 1 + t} \\ {3 – t} \\ {1 – 2t} \end{array}} \right)\)
Note: Award A1 for the form \({\mathbf{a}} + t{\mathbf{b}}\), A1 for the form \(L = {\mathbf{a}} + t{\mathbf{b}}\), A0 for the form \({\mathbf{r}} = {\mathbf{b}} + t{\mathbf{a}}\).
METHOD 1
valid approach (M1)
eg\(\;\;\;\left( {\begin{array}{*{20}{c}} { – 1} \\ 3 \\ 1 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 1 \\ { – 1} \\ { – 2} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 \\ y \\ { – 1} \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} 0 \\ y \\ { – 1} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { – 2} \\ 4 \\ 3 \end{array}} \right) + s\left( {\begin{array}{*{20}{c}} 1 \\ { – 1} \\ { – 2} \end{array}} \right)\)
one correct equation from their approach A1
eg\(\;\;\; – 1 + t = 0,{\text{ }}1 – 2t = – 1,{\text{ }} – 2 + s = 0,{\text{ }}3 – 2s = – 1\)
one correct value for their parameter and equation A1
eg\(\;\;\;t = 1,{\text{ }}s = 2\)
correct substitution A1
eg\(\;\;\;3 + 1( – 1),{\text{ }}4 + 2( – 1)\)
\(y = 2\) AG N0
METHOD 2
valid approach (M1)
eg\(\;\;\;\overrightarrow {{\text{AC}}} = k\overrightarrow {{\text{AB}}} \)
correct working A1
eg\(\;\;\;\overrightarrow {{\text{AC}}} = \left( {\begin{array}{*{20}{c}} 2 \\ {y – 4} \\ { – 4} \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} 2 \\ {y – 4} \\ { – 4} \end{array}} \right) = k\left( {\begin{array}{*{20}{c}} 1 \\ { – 1} \\ { – 2} \end{array}} \right)\)
\(k = 2\) A1
correct substitution A1
eg\(\;\;\;y – 4 = – 2\)
\(y = 2\) AG N0
[4 marks]
(i) correct substitution A1
eg\(\;\;\;0(1) + 2( – 1) – 1( – 2),{\text{ }}0 – 2 + 2\)
\(\overrightarrow {{\text{OC}}} \bullet \overrightarrow {{\text{AB}}} = 0\) A1 N1
(ii) \(9{0^ \circ }\) or \(\frac{\pi }{2}\) A1 N1
[3 marks]
METHOD 1 \({\text{(area}} = 0.5 \times {\text{height}} \times {\text{base)}}\)
\(\left| {\overrightarrow {{\text{OC}}} } \right| = \sqrt {0 + {2^2} + {{( – 1)}^2}} \;\;\;\left( { = \sqrt 5 } \right)\;\;\;\)(seen anywhere) A1
valid approach (M1)
eg\(\;\;\;\frac{1}{2} \times \left| {\overrightarrow {{\text{AB}}} } \right| \times \left| {\overrightarrow {{\text{OC}}} } \right|,{\text{ }}\left| {\overrightarrow {{\text{OC}}} } \right|\) is height of triangle
correct substitution A1
eg\(\;\;\;\frac{1}{2} \times \sqrt 6 \times \sqrt {0 + {{(2)}^2} + {{( – 1)}^2}} ,{\text{ }}\frac{1}{2} \times \sqrt 6 \times \sqrt 5 \)
area is \(\frac{{\sqrt {30} }}{2}\) A1 N2
METHOD 2 (difference of two areas)
one correct magnitude (seen anywhere) A1
eg\(\;\;\;\left| {\overrightarrow {{\text{OC}}} } \right| = \sqrt {{2^2} + {{( – 1)}^2}} \;\;\;\left( { = \sqrt 5 } \right),\;\;\;\left| {\overrightarrow {{\text{AC}}} } \right| = \sqrt {4 + 4 + 16} \;\;\;\left( { = \sqrt {24} } \right),\;\;\;\left| {\overrightarrow {{\text{BC}}} } \right| = \sqrt 6 \)
valid approach (M1)
eg\(\;\;\;\Delta {\text{OAC}} – \Delta {\text{OBC}}\)
correct substitution A1
eg\(\;\;\;\frac{1}{2} \times \sqrt {24} \times \sqrt 5 – \frac{1}{2} \times \sqrt 5 \times \sqrt 6 \)
area is \(\frac{{\sqrt {30} }}{2}\) A1 N2
METHOD 3 \({\text{(area}} = \frac{1}{2}ab\sin C{\text{ for }}\Delta {\text{OAB)}}\)
one correct magnitude of \(\overrightarrow {{\text{OA}}} \) or \(\overrightarrow {{\text{OB}}} \) (seen anywhere) A1
eg\(\;\;\;\left| {\overrightarrow {{\text{OA}}} } \right| = \sqrt {{{( – 2)}^2} + {4^2} + {3^2}} \;\;\;\left( { = \sqrt {29} } \right),\;\;\;\left| {\overrightarrow {{\text{OB}}} } \right| = \sqrt {1 + 9 + 1} \;\;\;\left( { = \sqrt {11} } \right)\)
valid attempt to find \(\cos \theta \) or \(\sin \theta \) (M1)
eg\(\;\;\;\cos {\text{C}} = \frac{{ – 1 – 3 – 2}}{{\sqrt 6 \times \sqrt {11} }}\;\;\;\left( { = \frac{{ – 6}}{{\sqrt {66} }}} \right),\;\;\;29 = 6 + 11 – 2\sqrt 6 \sqrt {11} \cos \theta ,{\text{ }}\frac{{\sin \theta }}{{\sqrt 5 }} = \frac{{\sin 90}}{{\sqrt {29} }}\)
correct substitution into \(\frac{1}{2}ab\sin {\text{C}}\) A1
eg\(\;\;\;\frac{1}{2} \times \sqrt 6 \times \sqrt {11} \times \sqrt {1 – \frac{{36}}{{66}}} ,{\text{ }}0.5 \times \sqrt 6 \times \sqrt {29} \times \frac{{\sqrt 5 }}{{\sqrt {29} }}\)
area is \(\frac{{\sqrt {30} }}{2}\) A1 N2
[4 marks]
Total [16 marks]
Question
The position vectors of points P and Q are i \( + \) 2 j \( – \) k and 7i \( + \) 3j \( – \) 4k respectively.
Find a vector equation of the line that passes through P and Q.
The line through P and Q is perpendicular to the vector 2i \( + \) nk. Find the value of \(n\).
Answer/Explanation
Markscheme
valid attempt to find direction vector (M1)
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{PQ}}} ,{\text{ }}\overrightarrow {{\text{QP}}} \)
correct direction vector (or multiple of) (A1)
eg\(\,\,\,\,\,\)6i \( + \) j \( – \) 3k
any correct equation in the form r \( = \) a \( + \) tb (any parameter for \(t\)) A2 N3
where a is i \( + \) 2j \( – \) k or 7i \( + \) 3j \( – \) 4k , and b is a scalar multiple of 6i \( + \) j \( – \) 3k
eg\(\,\,\,\,\,\)r \( = \) 7i \( + \) 3j \( – \) 4k \( + \) t(6i \( + \) j \( – \) 3k), r \( = \left( {\begin{array}{*{20}{c}} {1 + 6s} \\ {2 + 1s} \\ { – 1 – 3s} \end{array}} \right),{\text{ }}r = \left( {\begin{array}{*{20}{c}} 1 \\ 2 \\ { – 1} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} { – 6} \\ { – 1} \\ 3 \end{array}} \right)\)
Notes: Award A1 for the form a \( + \) tb, A1 for the form L \( = \) a \( + \) tb, A0 for the form r \( = \) b \( + \) ta.
[4 marks]
correct expression for scalar product (A1)
eg\(\,\,\,\,\,\)\(6 \times 2 + 1 \times 0 + ( – 3) \times n,{\text{ }} – 3n + 12\)
setting scalar product equal to zero (seen anywhere) (M1)
eg\(\,\,\,\,\,\)u \( \bullet \) v \( = 0,{\text{ }} – 3n + 12 = 0\)
\(n = 4\) A1 N2
[3 marks]
Question
A line \({L_1}\) passes through the points \({\text{A}}(0,{\text{ }}1,{\text{ }}8)\) and \({\text{B}}(3,{\text{ }}5,{\text{ }}2)\).
Given that \({L_1}\) and \({L_2}\) are perpendicular, show that \(p = 2\).
Find \(\overrightarrow {AB} \).
Hence, write down a vector equation for \({L_1}\).
A second line \({L_2}\), has equation r = \(\left( {\begin{array}{*{20}{c}} 1 \\ {13} \\ { – 14} \end{array}} \right) + s\left( {\begin{array}{*{20}{c}} p \\ 0 \\ 1 \end{array}} \right)\).
Given that \({L_1}\) and \({L_2}\) are perpendicular, show that \(p = 2\).
The lines \({L_1}\) and \({L_1}\) intersect at \(C(9,{\text{ }}13,{\text{ }}z)\). Find \(z\).
Find a unit vector in the direction of \({L_2}\).
Hence or otherwise, find one point on \({L_2}\) which is \(\sqrt 5 \) units from C.
Answer/Explanation
Markscheme
valid approach (M1)
eg \(A – B,\,\, – \left( \begin{gathered}
0 \hfill \\
1 \hfill \\
8 \hfill \\
\end{gathered} \right) + \left( \begin{gathered}
3 \hfill \\
5 \hfill \\
2 \hfill \\
\end{gathered} \right)\)
\(\overrightarrow {AB} = \left( \begin{gathered}
3 \hfill \\
4 \hfill \\
– 6 \hfill \\
\end{gathered} \right)\) A1 N2
[2 marks]
any correct equation in the form r = a + tb (any parameter for \(t\)) A2 N2
where a is \(\left( \begin{gathered}
0 \hfill \\
1 \hfill \\
8 \hfill \\
\end{gathered} \right)\) or \(\left( \begin{gathered}
3 \hfill \\
5 \hfill \\
2 \hfill \\
\end{gathered} \right)\), and b is a scalar multiple of \(\left( \begin{gathered}
3 \hfill \\
4 \hfill \\
– 6 \hfill \\
\end{gathered} \right)\)
eg\(\,\,\,\,\,\)r = \(\left( {\begin{array}{*{20}{c}} 0 \\ 1 \\ 8 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 3 \\ 4 \\ { – 6} \end{array}} \right)\), r = \(\left( {\begin{array}{*{20}{c}} {3 + 3t} \\ {5 + 4t} \\ {2 – 6t} \end{array}} \right)\), r = j + 8k + t(3i + 4j – 6k)
Note: Award A1 for the form a + tb, A1 for the form L = a + tb, A0 for the form r = b + ta.
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(a \bullet b = 0\)
choosing correct direction vectors (may be seen in scalar product) A1
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} 3 \\ 4 \\ { – 6} \end{array}} \right)\) and \(\left( {\begin{array}{*{20}{c}} p \\ 0 \\ 1 \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} 3 \\ 4 \\ { – 6} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} p \\ 0 \\ 1 \end{array}} \right) = 0\)
correct working/equation A1
eg\(\,\,\,\,\,\)\(3p – 6 = 0\)
\(p = 2\) AG N0
[3 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\({L_1} = \left( {\begin{array}{*{20}{c}} 9 \\ {13} \\ z \end{array}} \right),{\text{ }}{L_1} = {L_2}\)
one correct equation (must be different parameters if both lines used) (A1)
eg\(\,\,\,\,\,\)\(3t = 9,{\text{ }}1 + 2s = 9,{\text{ }}5 + 4t = 13,{\text{ }}3t = 1 + 2s\)
one correct value A1
eg\(\,\,\,\,\,\)\(t = 3,{\text{ }}s = 4,{\text{ }}t = 2\)
valid approach to substitute their \(t\) or \(s\) value (M1)
eg\(\,\,\,\,\,\)\(8 + 3( – 6),{\text{ }} – 14 + 4(1)\)
\(z = – 10\) A1 N3
[5 marks]
\(\left| {\vec d} \right| = \sqrt {{2^2} + 1} \,\,\left( { = \sqrt 5 } \right)\) (A1)
\(\frac{1}{{\sqrt 5 }}\left( {\begin{array}{*{20}{c}} 2 \\ 0 \\ 1 \end{array}} \right)\,\,\,\,\,\left( {{\text{accept}}\left( {\begin{array}{*{20}{c}} {\frac{2}{{\sqrt 5 }}} \\ {\frac{0}{{\sqrt 5 }}} \\ {\frac{1}{{\sqrt 5 }}} \end{array}} \right)} \right)\) A1 N2
[2 marks]
METHOD 1 (using unit vector)
valid approach (M1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} 9 \\ {13} \\ { – 10} \end{array}} \right) \pm \sqrt 5 \hat d\)
correct working (A1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} 9 \\ {13} \\ { – 10} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 2 \\ 0 \\ 1 \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} 9 \\ {13} \\ { – 10} \end{array}} \right) – \left( {\begin{array}{*{20}{c}} 2 \\ 0 \\ 1 \end{array}} \right)\)
one correct point A1 N2
eg\(\,\,\,\,\,\)\((11,{\text{ }}13,{\text{ }} – 9),{\text{ }}(7,{\text{ }}13,{\text{ }} – 11)\)
METHOD 2 (distance between points)
attempt to use distance between \((1 + 2s,{\text{ }}13,{\text{ }} – 14 + s)\) and \((9,{\text{ }}13,{\text{ }} – 10)\) (M1)
eg\(\,\,\,\,\,\)\({(2s – 8)^2} + {0^2} + {(s – 4)^2} = 5\)
solving \(5{s^2} – 40s + 75 = 0\) leading to \(s = 5\) or \(s = 3\) (A1)
one correct point A1 N2
eg\(\,\,\,\,\,\)\((11,{\text{ }}13,{\text{ }} – 9),{\text{ }}(7,{\text{ }}13,{\text{ }} – 11)\)
[3 marks]
Question
A line \(L\) passes through points \({\text{A}}( – 3,{\text{ }}4,{\text{ }}2)\) and \({\text{B}}( – 1,{\text{ }}3,{\text{ }}3)\).
The line \(L\) also passes through the point \({\text{C}}(3,{\text{ }}1,{\text{ }}p)\).
Show that \(\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 2 \\ { – 1} \\ 1 \end{array}} \right)\).
Find a vector equation for \(L\).
Find the value of \(p\).
The point D has coordinates \(({q^2},{\text{ }}0,{\text{ }}q)\). Given that \(\overrightarrow {{\text{DC}}} \) is perpendicular to \(L\), find the possible values of \(q\).
Answer/Explanation
Markscheme
correct approach A1
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} { – 1} \\ 3 \\ 3 \end{array}} \right) – \left( {\begin{array}{*{20}{c}} { – 3} \\ 4 \\ 2 \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} 3 \\ { – 4} \\ { – 2} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} { – 1} \\ 3 \\ 3 \end{array}} \right)\)
\(\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 2 \\ { – 1} \\ 1 \end{array}} \right)\) AG N0
[1 mark]
any correct equation in the form \(r = a + tb\) (any parameter for \(t\))
where \(a\) is \(\left( {\begin{array}{*{20}{c}} { – 3} \\ 4 \\ 2 \end{array}} \right)\) or \(\left( {\begin{array}{*{20}{c}} { – 1} \\ 3 \\ 3 \end{array}} \right)\) and \(b\) is a scalar multiple of \(\left( {\begin{array}{*{20}{c}} 2 \\ { – 1} \\ 1 \end{array}} \right)\) A2 N2
eg\(\,\,\,\,\,\)\(r = \left( {\begin{array}{*{20}{c}} { – 3} \\ 4 \\ 2 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 2 \\ { – 1} \\ 1 \end{array}} \right),{\text{ }}(x,{\text{ }}y,{\text{ }}z) = ( – 1,{\text{ }}3,{\text{ }}3) + s( – 2,{\text{ }}1,{\text{ }} – 1),{\text{ }}r = \left( {\begin{array}{*{20}{c}} { – 3 + 2t} \\ {4 – t} \\ {2 + t} \end{array}} \right)\)
Note: Award A1 for the form \(a + tb\), A1 for the form \(L = a + tb\), A0 for the form \(r = b + ta\).
[2 marks]
METHOD 1 – finding value of parameter
valid approach (M1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} { – 3} \\ 4 \\ 2 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 2 \\ { – 1} \\ 1 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ p \end{array}} \right),{\text{ }}( – 1,{\text{ }}3,{\text{ }}3) + s( – 2,{\text{ }}1,{\text{ }} – 1) = (3,{\text{ }}1,{\text{ }}p)\)
one correct equation (not involving \(p\)) (A1)
eg\(\,\,\,\,\,\)\( – 3 + 2t = 3,{\text{ }} – 1 – 2s = 3,{\text{ }}4 – t = 1,{\text{ }}3 + s = 1\)
correct parameter from their equation (may be seen in substitution) A1
eg\(\,\,\,\,\,\)\(t = 3,{\text{ }}s = – 2\)
correct substitution (A1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} { – 3} \\ 4 \\ 2 \end{array}} \right) + 3\left( {\begin{array}{*{20}{c}} 2 \\ { – 1} \\ 1 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ p \end{array}} \right),{\text{ }}3 – ( – 2)\)
\(p = 5\,\,\,\,\,\left( {{\text{accept }}\left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ 5 \end{array}} \right)} \right)\) A1 N2
METHOD 2 – eliminating parameter
valid approach (M1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} { – 3} \\ 4 \\ 2 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 2 \\ { – 1} \\ 1 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ p \end{array}} \right),{\text{ }}( – 1,{\text{ }}3,{\text{ }}3) + s( – 2,{\text{ }}1,{\text{ }} – 1) = (3,{\text{ }}1,{\text{ }}p)\)
one correct equation (not involving \(p\)) (A1)
eg\(\,\,\,\,\,\)\( – 3 + 2t = 3,{\text{ }} – 1 – 2s = 3,{\text{ }}4 – t = 1,{\text{ }}3 + s = 1\)
correct equation (with \(p\)) A1
eg\(\,\,\,\,\,\)\(2 + t = p,{\text{ }}3 – s = p\)
correct working to solve for \(p\) (A1)
eg\(\,\,\,\,\,\)\(7 = 2p – 3,{\text{ }}6 = 1 + p\)
\(p = 5\,\,\,\,\,\left( {{\text{accept }}\left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ 5 \end{array}} \right)} \right)\) A1 N2
[5 marks]
valid approach to find \(\overrightarrow {{\text{DC}}} \) or \(\overrightarrow {{\text{CD}}} \) (M1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ 5 \end{array}} \right) – \left( {\begin{array}{*{20}{c}} {{q^2}} \\ 0 \\ q \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} {{q^2}} \\ 0 \\ q \end{array}} \right) – \left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ 5 \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} {{q^2}} \\ 0 \\ q \end{array}} \right) – \left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ p \end{array}} \right)\)
correct vector for \(\overrightarrow {{\text{DC}}} \) or \(\overrightarrow {{\text{CD}}} \) (may be seen in scalar product) A1
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} {3 – {q^2}} \\ 1 \\ {5 – q} \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} {{q^2} – 3} \\ { – 1} \\ {q – 5} \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} {3 – {q^2}} \\ 1 \\ {p – q} \end{array}} \right)\)
recognizing scalar product of \(\overrightarrow {{\text{DC}}} \) or \(\overrightarrow {{\text{CD}}} \) with direction vector of \(L\) is zero (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} {3 – {q^2}} \\ 1 \\ {p – q} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} 2 \\ { – 1} \\ 1 \end{array}} \right) = 0,{\text{ }}\overrightarrow {{\text{DC}}} \bullet \overrightarrow {{\text{AC}}} = 0,{\text{ }}\left( {\begin{array}{*{20}{c}} {3 – {q^2}} \\ 1 \\ {5 – q} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} 2 \\ { – 1} \\ 1 \end{array}} \right) = 0\)
correct scalar product in terms of only \(q\) A1
eg\(\,\,\,\,\,\)\(6 – 2{q^2} – 1 + 5 – q,{\text{ }}2{q^2} + q – 10 = 0,{\text{ }}2(3 – {q^2}) – 1 + 5 – q\)
correct working to solve quadratic (A1)
eg\(\,\,\,\,\,\)\((2q + 5)(q – 2),{\text{ }}\frac{{ – 1 \pm \sqrt {1 – 4(2)( – 10)} }}{{2(2)}}\)
\(q = – \frac{5}{2},{\text{ }}2\) A1A1 N3
[7 marks]
Question
Let \(\mathop {{\text{OA}}}\limits^ \to = \left( \begin{gathered}
2 \hfill \\
1 \hfill \\
3 \hfill \\
\end{gathered} \right)\) and \(\mathop {{\text{AB}}}\limits^ \to = \left( \begin{gathered}
1 \hfill \\
3 \hfill \\
1 \hfill \\
\end{gathered} \right)\), where O is the origin. L1 is the line that passes through A and B.
Find a vector equation for L1.
The vector \(\left( \begin{gathered}
2 \hfill \\
p \hfill \\
0 \hfill \\
\end{gathered} \right)\) is perpendicular to \(\mathop {{\text{AB}}}\limits^ \to \). Find the value of p.
Answer/Explanation
Markscheme
any correct equation in the form r = a + tb (accept any parameter for t)
where a is \(\left( \begin{gathered}
2 \hfill \\
1 \hfill \\
3 \hfill \\
\end{gathered} \right)\), and b is a scalar multiple of \(\left( \begin{gathered}
1 \hfill \\
3 \hfill \\
1 \hfill \\
\end{gathered} \right)\) A2 N2
eg r = \(\left( \begin{gathered}
2 \hfill \\
1 \hfill \\
3 \hfill \\
\end{gathered} \right) = t\left( \begin{gathered}
1 \hfill \\
3 \hfill \\
1 \hfill \\
\end{gathered} \right)\), r = 2i + j + 3k + s(i + 3j + k)
Note: Award A1 for the form a + tb, A1 for the form L = a + tb, A0 for the form r = b + ta.
[2 marks]
METHOD 1
correct scalar product (A1)
eg (1 × 2) + (3 × p) + (1 × 0), 2 + 3p
evidence of equating their scalar product to zero (M1)
eg a•b = 0, 2 + 3p = 0, 3p = −2
\(p = – \frac{2}{3}\) A1 N3
METHOD 2
valid attempt to find angle between vectors (M1)
correct substitution into numerator and/or angle (A1)
eg \({\text{cos}}\,\theta = \frac{{\left( {1 \times 2} \right) + \left( {3 \times p} \right) + \left( {1 \times 0} \right)}}{{\left| a \right|\left| b \right|}},\,\,{\text{cos}}\,\theta = 0\)
\(p = – \frac{2}{3}\) A1 N3
[3 marks]
