Question
The point O has coordinates (0 , 0 , 0) , point A has coordinates (1 , – 2 , 3) and point B has coordinates (– 3 , 4 , 2) .
(i) Show that \(\overrightarrow {{\rm{AB}}} = \left( {\begin{array}{*{20}{c}}
{ – 4}\\
6\\
{ – 1}
\end{array}} \right)\) .
(ii) Find \({\rm{B}}\widehat {\rm{A}}{\rm{O}}\) .
The line \({L_1}\) has equation \(\left( {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 3}\\
4\\
2
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
{ – 4}\\
6\\
{ – 1}
\end{array}} \right)\) .
Write down the coordinates of two points on \({L_1}\) .
The line \({L_2}\) passes through A and is parallel to \(\overrightarrow {{\rm{OB}}} \) .
(i) Find a vector equation for \({L_2}\) , giving your answer in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) .
(ii) Point \(C(k, – k,5)\) is on \({L_2}\) . Find the coordinates of C.
The line \({L_3}\) has equation \(\left( {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
3\\
{ – 8}\\
0
\end{array}} \right) + p\left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
{ – 1}
\end{array}} \right)\) and passes through the point C.
Find the value of p at C.
Answer/Explanation
Markscheme
(i) evidence of approach M1
e.g. \(\overrightarrow {{\rm{AO}}} + \overrightarrow {{\rm{OB}}} = \overrightarrow {{\rm{AB}}} \)
\(\overrightarrow {{\rm{AB}}} = \left( {\begin{array}{*{20}{c}}
{ – 4}\\
6\\
{ – 1}
\end{array}} \right)\) AG N0
(ii) for choosing correct vectors, (\(\overrightarrow {{\rm{AO}}} \) with \(\overrightarrow {{\rm{AB}}} \) or \(\overrightarrow {{\rm{OA}}} \) with \(\overrightarrow {{\rm{BA}}} \) ) (A1)(A1)
Note: Using \(\overrightarrow {{\rm{AO}}} \) with \(\overrightarrow {{\rm{BA}}} \) will lead to \(\pi – 0.799\) . If they then say \({\rm{B}}\widehat {\rm{A}}{\rm{O}} = 0.799\) , this is a correct solution.
calculating \(\overrightarrow {{\rm{AO}}} \bullet \overrightarrow {{\rm{AB}}} \) , \(\left| {\overrightarrow {{\rm{AO}}} } \right|\) , \(\left| {\overrightarrow {{\rm{AB}}} } \right|\) (A1)(A1)(A1)
e.g. \({d_1} \bullet {d_2} = ( – 1)( – 4) + (2)(6) + ( – 3)( – 1)( = 19)\)
\(\left| {{d_1}} \right| = \sqrt {{{( – 1)}^2} + {2^2} + {{( – 3)}^2}} ( = \sqrt {14} )\) , \(\left| {{d_2}} \right| = \sqrt {{{( – 4)}^2} + {6^2} + {{( – 1)}^2}} ( = \sqrt {53} )\)
evidence of using the formula to find the angle M1
e.g. \(\cos \theta = \frac{{( – 1)( – 4) + (2)(6) + ( – 3)( – 1)}}{{\sqrt {{{( – 1)}^2} + {2^2} + {{( – 3)}^2}} \sqrt {{{( – 4)}^2} + {6^2} + {{( – 1)}^2}} }}\) , \(\frac{{19}}{{\sqrt {14} \sqrt {53} }}\) , \(0.69751 \ldots \)
\({\rm{B}}\widehat {\rm{A}}{\rm{O}} = 0.799\) radians (accept \(45.8^\circ \)) A1 N3
[8 marks]
two correct answers A1A1
e.g. (1, \( – 2\), 3) , (\( – 3\), 4, 2) , (\( – 7\), 10, 1), (\( – 11\), 16, 0) N2
[2 marks]
(i) \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
3
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
{ – 3}\\
4\\
2
\end{array}} \right)\) A2 N2
(ii) C on \({L_2}\) , so \(\left( {\begin{array}{*{20}{c}}
k\\
{ – k}\\
5
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
3
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
{ – 3}\\
4\\
2
\end{array}} \right)\) (M1)
evidence of equating components (A1)
e.g. \(1 – 3t = k\) , \( – 2 + 4t = – k\) , \(5 = 3 + 2t\)
one correct value \(t = 1\) , \(k = – 2\) (seen anywhere) (A1)
coordinates of C are \(( – 2{\text{, }}2{\text{, }}5)\) A1 N3
[6 marks]
for setting up one (or more) correct equation using \(\left( {\begin{array}{*{20}{c}}
{ – 2}\\
2\\
5
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
3\\
{ – 8}\\
0
\end{array}} \right) + p\left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
{ – 1}
\end{array}} \right)\) (M1)
e.g. \(3 + p = – 2\) , \( – 8 – 2p = 2\) , \( – p = 5\)
\(p = – 5\) A1 N2
[2 marks]
Question
Consider the points P(2, −1, 5) and Q(3, − 3, 8). Let \({L_1}\) be the line through P and Q.
Show that \(\overrightarrow {{\rm{PQ}}} = \left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
3
\end{array}} \right)\) .
The line \({L_1}\) may be represented by \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
3 \\
{ – 3} \\
8
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
1 \\
{ – 2} \\
3
\end{array}} \right)\) .
(i) What information does the vector \(\left( {\begin{array}{*{20}{c}}
3\\
{ – 3}\\
8
\end{array}} \right)\) give about \({L_1}\) ?
(ii) Write down another vector representation for \({L_1}\) using \(\left( {\begin{array}{*{20}{c}}
3\\
{ – 3}\\
8
\end{array}} \right)\) .
The point \({\text{T}}( – 1{\text{, }}5{\text{, }}p)\) lies on \({L_1}\) .
Find the value of \(p\) .
The point T also lies on \({L_2}\) with equation \(\left( {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 3}\\
9\\
2
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
q
\end{array}} \right)\) .
Show that \(q = – 3\) .
Let \(\theta \) be the obtuse angle between \({L_1}\) and \({L_2}\) . Calculate the size of \(\theta \) .
Answer/Explanation
Markscheme
evidence of correct approach A1
e.g. \(\overrightarrow {{\rm{PQ}}} = \overrightarrow {{\rm{OQ}}} – \overrightarrow {{\rm{OP}}} \) , \(\left( {\begin{array}{*{20}{c}}
3\\
{ – 3}\\
8
\end{array}} \right) – \left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
5
\end{array}} \right)\)
\(\overrightarrow {{\rm{PQ}}} = \left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
3
\end{array}} \right)\) AG N0
[1 mark]
(i) correct description R1 N1
e.g. reference to \(\left( {\begin{array}{*{20}{c}}
3\\
{ – 3}\\
8
\end{array}} \right)\) being the position vector of a point on the line, a vector to the line, a point on the line.
(ii) any correct expression in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) A2 N2
where \({\boldsymbol{a}}\) is \(\left( {\begin{array}{*{20}{c}}
3 \\
{ – 3} \\
8
\end{array}} \right)\) , and \({\boldsymbol{b}}\) is a scalar multiple of \(\left( {\begin{array}{*{20}{c}}
1 \\
{ – 2} \\
3
\end{array}} \right)\)
e.g. \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
3 \\
{ – 3} \\
8
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
{ – 1} \\
2 \\
{ – 3}
\end{array}} \right)\) , \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{3 + 2s} \\
{ – 3 – 4s} \\
{8 + 6s}
\end{array}} \right)\)
[3 marks]
one correct equation (A1)
e.g. \(3 + s = – 1\) , \( – 3 – 2s = 5\)
\(s = – 4\) A1
\(p = – 4\) A1 N2
[3 marks]
one correct equation A1
e.g. \( – 3 + t = – 1\) , \(9 – 2t = 5\)
\(t = 2\) A1
substituting \(t = 2\)
e.g. \(2 + 2q = – 4\) , \(2q = – 6\) A1
\(q = – 3\) AG N0
[3 marks]
choosing correct direction vectors \(\left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
3
\end{array}} \right)\) and \(\left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
{ – 3}
\end{array}} \right)\) (A1)(A1)
finding correct scalar product and magnitudes (A1)(A1)(A1)
scalar product \((1)(1) + ( – 2)( – 2) + ( – 3)(3)\) \(( = – 4)\)
magnitudes \(\sqrt {{1^2} + {{( – 2)}^2} + {3^2}} \) \( = \sqrt {14} \) , \(\sqrt {{1^2} + {{( – 2)}^2} + {{( – 3)}^2}} \) \( = \sqrt {14} \)
evidence of substituting into scalar product M1
e.g. \(\cos \theta = \frac{{ – 4}}{{3.741 \ldots \times 3.741 \ldots }}\)
\(\theta = 1.86\) radians (or \(107^\circ \)) A1 N4
[7 marks]
Question
In this question, distance is in metres.
Toy airplanes fly in a straight line at a constant speed. Airplane 1 passes through a point A.
Its position, p seconds after it has passed through A, is given by \(\left( {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
3\\
{ – 4}\\
0
\end{array}} \right) + p\left( {\begin{array}{*{20}{c}}
{ – 2}\\
3\\
1
\end{array}} \right)\) .
(i) Write down the coordinates of A.
(ii) Find the speed of the airplane in \({\text{m}}{{\text{s}}^{ – 1}}\).
After seven seconds the airplane passes through a point B.
(i) Find the coordinates of B.
(ii) Find the distance the airplane has travelled during the seven seconds.
Airplane 2 passes through a point C. Its position q seconds after it passes through C is given by \(\left( {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
2\\
{ – 5}\\
8
\end{array}} \right) + q\left( {\begin{array}{*{20}{c}}
{ – 1}\\
2\\
a
\end{array}} \right),a \in \mathbb{R}\) .
The angle between the flight paths of Airplane 1 and Airplane 2 is \({40^ \circ }\) . Find the two values of a.
Answer/Explanation
Markscheme
(i) (3, \( – 4\), 0) A1 N1
(ii) choosing velocity vector \(\left( {\begin{array}{*{20}{c}}
{ – 2}\\
3\\
1
\end{array}} \right)\) (M1)
finding magnitude of velocity vector (A1)
e.g. \(\sqrt {{{( – 2)}^2} + {3^2} + {1^2}} \) , \(\sqrt {4 + 9 + 1} \)
speed \(= 3.74\) \(\left( {\sqrt {14} } \right)\) A1 N2
[4 marks]
(i) substituting \(p = 7\) (M1)
\({\text{B}} = ( – 11{\text{, }}17{\text{, }}7)\) A1 N2
(ii) METHOD 1
appropriate method to find \(\overrightarrow {{\rm{AB}}} \) or \(\overrightarrow {{\rm{BA}}} \) (M1)
e.g. \(\overrightarrow {{\rm{AO}}} + \overrightarrow {{\rm{OB}}} \) , \({\rm{A}} – {\rm{B}}\)
\(\overrightarrow {{\rm{AB}}} = \left( {\begin{array}{*{20}{c}}
{ – 14}\\
{21}\\
7
\end{array}} \right)\) or \(\overrightarrow {{\rm{BA}}} = \left( {\begin{array}{*{20}{c}}
{14}\\
{ – 21}\\
{ – 7}
\end{array}} \right)\) (A1)
distance \(= 26.2\) \(\left( {7\sqrt {14} } \right)\) A1 N3
METHOD 2
evidence of applying distance is speed × time (M2)
e.g. \(3.74 \times 7\)
distance \(= 26.2\) \(\left( {7\sqrt {14} } \right)\) A1 N3
METHOD 3
attempt to find AB2 , AB (M1)
e.g. \({(3 – ( – 11))^2} + {( – 4 – 17)^2} + (0 – 7){)^2}\) , \(\sqrt {{{(3 – ( – 11))}^2} + {{( – 4 – 17)}^2} + (0 – 7){)^2}} \)
AB2 \(= 686\), AB \(= \sqrt {686} \) (A1)
distance AB \(= 26.2\) \(\left( {7\sqrt {14} } \right)\) A1 N3
[5 marks]
correct direction vectors \(\left( {\begin{array}{*{20}{c}}
{ – 2}\\
3\\
1
\end{array}} \right)\) and \(\left( {\begin{array}{*{20}{c}}
{ – 1}\\
2\\
a
\end{array}} \right)\) (A1)(A1)
\(\left| {\begin{array}{*{20}{c}}
{ – 1}\\
2\\
a
\end{array}} \right| = \sqrt {{a^2} + 5} \) , \(\left( {\begin{array}{*{20}{c}}
{ – 2}\\
3\\
1
\end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}}
{ – 1}\\
2\\
a
\end{array}} \right) = a + 8\) (A1)(A1)
substituting M1
e.g. \(\cos {40^ \circ } = \frac{{a + 8}}{{\sqrt {14} \sqrt {{a^2} + 5} }}\)
\(a = 3.21\) , \(a = – 0.990\) A1A1 N3
[7 marks]
Question
Line \({L_1}\) passes through points \({\text{A}}(1{\text{, }} – 1{\text{, }}4)\) and \({\text{B}}(2{\text{, }} – 2{\text{, }}5)\) .
Line \({L_2}\) has equation \({\boldsymbol{r}} = \left( \begin{array}{l}
2\\
4\\
7
\end{array} \right) + s\left( \begin{array}{l}
2\\
1\\
3
\end{array} \right)\) .
Find \(\overrightarrow {{\rm{AB}}} \) .
Find an equation for \({L_1}\) in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) .
Find the angle between \({L_1}\) and \({L_2}\) .
The lines \({L_1}\) and \({L_2}\) intersect at point C. Find the coordinates of C.
Answer/Explanation
Markscheme
appropriate approach (M1)
e.g. \(\overrightarrow {{\rm{AO}}} + \overrightarrow {{\rm{OB}}} \) , \(B – A\)
\(\overrightarrow {{\rm{AB}}} = \left( {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
1
\end{array}} \right)\) A1 N2
[2 marks]
any correct equation in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) A2 N2
where \({\boldsymbol{b}}\) is a scalar multiple of \(\left( {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
1
\end{array}} \right)\)
e.g. \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
4
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
1
\end{array}} \right)\) , \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{2 + t}\\
{ – 2 – t}\\
{5 + t}
\end{array}} \right)\) , \({\boldsymbol{r}} = 2{\boldsymbol{i}} – 2{\boldsymbol{j}} + 5{\boldsymbol{k}} + t({\boldsymbol{i}} – {\boldsymbol{j}} + {\boldsymbol{k}})\)
[2 marks]
choosing correct direction vectors \(\left( \begin{array}{l}
2\\
1\\
3
\end{array} \right)\) , \(\left( {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
1
\end{array}} \right)\) (A1)(A1)
finding scalar product and magnitudes (A1)(A1)(A1)
scalar product \( = 1 \times 2 + – 1 \times 1 + 1 \times 3\) \(\left( { = 4} \right)\)
magnitudes \(\sqrt {{1^2} + {{( – 1)}^2} + {1^2}}{\text{ }}( = 1.73 \ldots )\) , \(\sqrt {4 + 1 + 9}{\text{ }}( = 3.74 \ldots )\)
substitution into \(\frac{{{\boldsymbol{u}} \bullet {\boldsymbol{v}}}}{{|{\boldsymbol{u}}||{\boldsymbol{v}}|}}\) (accept \(\theta = \frac{{{\boldsymbol{u}} \bullet {\boldsymbol{v}}}}{{|{\boldsymbol{u}}||{\boldsymbol{v}}|}}\) , but not \(\sin \theta = \frac{{{\boldsymbol{u}} \bullet {\boldsymbol{v}}}}{{|{\boldsymbol{u}}||{\boldsymbol{v}}|}}\) ) M1
e.g. \(\cos \theta = \frac{{1 \times 2 + – 1 \times 1 + 1 \times 3}}{{\sqrt {{1^2} + {{( – 1)}^2} + {1^2}} \sqrt {{2^2} + {1^2} + {3^2}} }}\) , \(\cos \theta = \frac{4}{{\sqrt {42} }}\)
\(\theta = 0.906\) \(({51.9^ \circ })\) A1 N5
[7 marks]
METHOD 1 (from \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
1 \\
{ – 1} \\
4
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1 \\
{ – 1} \\
1
\end{array}} \right)\) )
appropriate approach (M1)
e.g. \({\boldsymbol{p}} = {\boldsymbol{r}}\) , \(\left( {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
4
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
1
\end{array}} \right)t = \left( {\begin{array}{*{20}{c}}
2\\
4\\
7
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
2\\
1\\
3
\end{array}} \right)s\)
two correct equations A1A1
e.g. \(1 + t = 2 + 2s\) , \( – 1 – t = 4 + s\) , \(4 + t = 7 + 3s\)
attempt to solve (M1)
one correct parameter A1
e.g. \(t = – 3\) , \(s = – 2\)
C is \(( – 2{\text{, }}2{\text{, }}1)\) A1 N3
METHOD 2 (from \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
2 \\
{ – 2} \\
5
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1 \\
{ – 1} \\
1
\end{array}} \right)\) )
appropriate approach (M1)
e.g. \({\boldsymbol{p}} = {\boldsymbol{r}}\) , \(\left( {\begin{array}{*{20}{c}}
2\\
{ – 2}\\
5
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
1
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
2\\
4\\
7
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
2\\
1\\
3
\end{array}} \right)s\)
two correct equations A1A1
e.g. \(2 + t = 2 + 2s\) , \( – 2 – t = 4 + s\) , \(5 + t = 7 + 3s\)
attempt to solve (M1)
one correct parameter A1
e.g. \(t = – 4\) , \(s = – 2\)
C is \(( – 2{\text{, }}2{\text{, }}1)\) A1 N3
[6 marks]
Question
The following diagram shows the cuboid (rectangular solid) OABCDEFG, where O is the origin, and \(\overrightarrow {{\rm{OA}}} = 4\boldsymbol{i}\) , \(\overrightarrow {{\rm{OC}}} = 3\boldsymbol{j}\) , \(\overrightarrow {{\rm{OD}}} = 2\boldsymbol{k}\) .
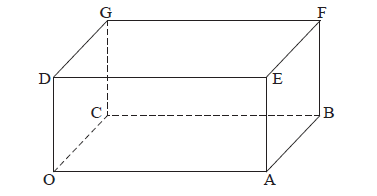
(i) Find \(\overrightarrow {{\rm{OB}}} \) .
(ii) Find \(\overrightarrow {{\rm{OF}}} \) .
(iii) Show that \(\overrightarrow {{\rm{AG}}} = – 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) .
Write down a vector equation for
(i) the line OF;
(ii) the line AG.
Find the obtuse angle between the lines OF and AG.
Answer/Explanation
Markscheme
(i) valid approach (M1)
e.g. \({\rm{OA + OB}}\)
\(\overrightarrow {{\rm{OB}}} = 4{\boldsymbol{i}} + 3{\boldsymbol{j}}\) A1 N2
(ii) valid approach (M1)
e.g. \(\overrightarrow {{\rm{OA}}} {\rm{ + }}\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{BF}}} \) ; \(\overrightarrow {{\rm{OB}}} {\rm{ + }}\overrightarrow {{\rm{BF}}} \) ; \(\overrightarrow {{\rm{OC}}} {\rm{ + }}\overrightarrow {{\rm{CG}}} {\rm{ + }}\overrightarrow {{\rm{GF}}} \)
\(\overrightarrow {{\rm{OF}}} = 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) A1 N2
(iii) correct approach A1
e.g. \(\overrightarrow {{\rm{AO}}} {\rm{ + }}\overrightarrow {{\rm{OC}}} {\rm{ + }}\overrightarrow {{\rm{CG}}} \) ; \(\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{BF}}} {\rm{ + }}\overrightarrow {{\rm{FG}}} \) ; \(\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{BC}}} {\rm{ + }}\overrightarrow {{\rm{CG}}} \)
\(\overrightarrow {{\rm{AG}}} = – 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) AG N0
[5 marks]
(i) any correct equation for (OF) in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) A2 N2
where \({\boldsymbol{a}}\) is 0 or \(4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) , and \({\boldsymbol{b}}\) is a scalar multiple of \(4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\)
e.g. \({\boldsymbol{r}} = t(4{\text{, }}3{\text{, }}2)\) , \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{4t}\\
{3t}\\
{2t}
\end{array}} \right)\) , \({\boldsymbol{r}} = 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}} + t(4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}})\)
(ii) any correct equation for (AG) in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + s{\boldsymbol{b}}\) A2 N2
where \({\boldsymbol{a}}\) is \(4{\boldsymbol{i}}\) or \(3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) and \({\boldsymbol{b}}\) is a scalar multiple of \( – 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\)
e.g. \({\boldsymbol{r}} = (4{\text{, }}0{\text{, }}0) + s( – 4{\text{, }}3{\text{, }}2)\) , \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{4 – 4s}\\
{3s}\\
{2s}
\end{array}} \right)\) , \({\boldsymbol{r}} = 3{\boldsymbol{j}} + 2{\boldsymbol{k}} + s( – 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}})\)
[4 marks]
choosing correct direction vectors, \(\overrightarrow {{\rm{OF}}} \) and \(\overrightarrow {{\rm{AG}}} \) (A1)(A1)
scalar product \( = – 16 + 9 + 4\) \(( = – 3)\) (A1)
magnitudes \(\sqrt {{4^2} + {3^2} + {2^2}} \) , \(\sqrt {{{( – 4)}^2} + {3^2} + {2^2}} \) , \(\left( {\sqrt {29} ,\sqrt {29} } \right)\) (A1)(A1)
substitution into formula M1
e.g. \(\cos \theta = \frac{{ – 16 + 9 + 4}}{{\left( {\sqrt {{4^2} + {3^2} + {2^2}} } \right) \times \sqrt {{{( – 4)}^2} + {3^2} + {2^2}} }} = \left( { – \frac{3}{{29}}} \right)\)
\(95.93777^\circ \) , \(1.67443{\text{ radians}}\)
\(\theta = 95.9^\circ \) or \(1.67\) A1 N4
[7 marks]
Question
Consider the points \({\text{A }}(1,{\text{ }}5,{\text{ }} – 7)\) and \({\text{B }}( – 9,{\text{ }}9,{\text{ }} – 6)\).
Let C be a point such that \(\overrightarrow {{\text{AC}}} = \left( {\begin{array}{*{20}{c}} 6 \\ { – 4} \\ 0 \end{array}} \right)\).
The line \(L\) passes through B and is parallel to (AC).
Find \(\overrightarrow {{\text{AB}}} \).
Find the coordinates of C.
Write down a vector equation for \(L\).
Given that \(\left| {\overrightarrow {{\text{AB}}} } \right| = k\left| {\overrightarrow {{\text{AC}}} } \right|\), find \(k\).
The point D lies on \(L\) such that \(\left| {\overrightarrow {{\text{AB}}} } \right| = \left| {\overrightarrow {{\text{BD}}} } \right|\). Find the possible coordinates of D.
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\({\text{B}} – {\text{A}},{\text{ AO}} + {\text{OB}},{\text{ }}\left( {\begin{array}{*{20}{c}} { – 9} \\ 9 \\ { – 6} \end{array}} \right) – \left( {\begin{array}{*{20}{c}} 1 \\ 5 \\ { – 7} \end{array}} \right)\)
\(\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} { – 10} \\ 4 \\ 1 \end{array}} \right)\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\({\text{OC}} = {\text{OA}} + {\text{AC}},{\text{ }}\left( {\begin{array}{*{20}{c}} {1 + 6} \\ {5 – 4} \\ { – 7 + 0} \end{array}} \right)\)
\({\text{C}}(7,{\text{ }}1,{\text{ }} – 7)\) A1 N2
[2 marks]
any correct equation in the form r \( = \) a \( + t\)b (accept any parameter for \(t\)
where a is \(\left( {\begin{array}{*{20}{c}} { – 9} \\ 9 \\ { – 6} \end{array}} \right)\), and b is a scalar multiple of \(\left( {\begin{array}{*{20}{c}} 6 \\ { – 4} \\ 0 \end{array}} \right)\) A2 N2
eg\(\,\,\,\,\,\)r \( = \left( {\begin{array}{*{20}{c}} { – 9} \\ 9 \\ { – 6} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 6 \\ { – 4} \\ 0 \end{array}} \right)\), r \( = – 9\)i \( + 9\)j \( – 6\)k \( + s(6\)i \( – 4\)j \( + 0\)k\()\)
[2 marks]
correct magnitudes (A1)(A1)
eg\(\,\,\,\,\,\)\(\sqrt {{{( – 10)}^2} + {{( – 4)}^2} + {1^2}} ,{\text{ }}\sqrt {{6^2} + {{( – 4)}^2} + {{(0)}^2}} ,{\text{ }}\sqrt {{{10}^2} + {4^2} + 1} ,{\text{ }}\sqrt {{6^2} + {4^2}} \)
\(k = \frac{{\sqrt {117} }}{{\sqrt {52} }}{\text{ }}( = 1.5){\text{ }}({\text{exact}})\) A1 N3
[3 marks]
correct interpretation of relationship between magnitudes (A1)
eg\(\,\,\,\,\,\)\({\text{AB}} = 1.5{\text{AC}},{\text{ BD}} = 1.5{\text{AC}},{\text{ }}\sqrt {117} = \sqrt {52{t^2}} \)
recognizing D can have two positions (may be seen in working) R1
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{BD}}} = 1.5\overrightarrow {{\text{AC}}} \) and \(\overrightarrow {{\text{BD}}} = – 1.5\overrightarrow {{\text{AC}}} ,{\text{ }}t = \pm 1.5\), diagram, two answers
valid approach (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{OD}}} = \overrightarrow {{\text{OB}}} + \overrightarrow {{\text{BD}}} {\text{, }}\left( {\begin{array}{*{20}{c}} { – 9} \\ 9 \\ { – 6} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 6 \\ { – 4} \\ 0 \end{array}} \right),{\text{ }}\overrightarrow {{\text{BD}}} = k\left( {\begin{array}{*{20}{c}} 6 \\ { – 4} \\ 0 \end{array}} \right)\)
one correct expression for \(\overrightarrow {{\text{OD}}} \) (A1)
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{OD}}} = \left( {\begin{array}{*{20}{c}} { – 9} \\ 9 \\ { – 6} \end{array}} \right) + 1.5\left( {\begin{array}{*{20}{c}} 6 \\ { – 4} \\ 0 \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} { – 9} \\ 9 \\ { – 6} \end{array}} \right) – 1.5\left( {\begin{array}{*{20}{c}} 6 \\ { – 4} \\ 0 \end{array}} \right)\)
\({\text{D}} = (0,{\text{ }}3,{\text{ }} – 6),{\text{ D}} = ( – 18,{\text{ }}15,{\text{ }} – 6)\) (accept position vectors) A1A1 N3
[6 marks]
Question
Consider the lines \({L_1}\) , \({L_2}\) , \({L_2}\) , and \({L_4}\) , with respective equations.
\({L_1}\) : \(\left( {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1\\
2\\
3
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
3\\
{ – 2}\\
1
\end{array}} \right)\)
\({L_2}\) : \(\left( \begin{array}{l}
x\\
y\\
z
\end{array} \right) = \left( \begin{array}{l}
1\\
2\\
3
\end{array} \right) + p\left( \begin{array}{l}
3\\
2\\
1
\end{array} \right)\)
\({L_3}\) : \(\left( {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
0\\
1\\
0
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
{ – 1}\\
2\\
{ – a}
\end{array}} \right)\)
\({L_4}\) : \(\left( {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right) = q\left( {\begin{array}{*{20}{c}}
{ – 6}\\
4\\
{ – 2}
\end{array}} \right)\)
Write down the line that is parallel to \({L_4}\) .
Write down the position vector of the point of intersection of \({L_1}\) and \({L_2}\) .
Given that \({L_1}\) is perpendicular to \({L_3}\) , find the value of a .
Answer/Explanation
Markscheme
\({L_1}\) A1 N1
[1 mark]
\(\left( \begin{array}{l}
1\\
2\\
3
\end{array} \right)\) A1 N1
[1 mark]
choosing correct direction vectors A1A1
e.g. \(\left( {\begin{array}{*{20}{c}}
3\\
{ – 2}\\
1
\end{array}} \right)\) , \(\left( {\begin{array}{*{20}{c}}
{ – 1}\\
2\\
{ – a}
\end{array}} \right)\)
recognizing that \({\boldsymbol{a}} \bullet {\boldsymbol{b}} = 0\) M1
correct substitution A1
e.g. \( – 3 – 4 – a = 0\)
\(a = – 7\) A1 N3
[5 marks]

