Question
Find the vector equation of the line of intersection of the three planes represented by the following system of equations.
\[2x – 7y + 5z = 1\]
\[6x + 3y – z = – 1\]
\[ – 14x – 23y + 13z = 5\]
Answer/Explanation
Markscheme
METHOD 1
(from GDC)
\(\left( {\begin{array}{*{20}{ccc|c}}
1&0&{\frac{1}{6}}&{ – \frac{1}{{12}}} \\
0&1&{ – \frac{2}{3}}&{ – \frac{1}{6}} \\
0&0&0&0
\end{array}} \right)\) (M1)
\(x + \frac{1}{6}\lambda = – \frac{1}{{12}}\) A1
\(y – \frac{2}{3}\lambda = – \frac{1}{6}\) A1
\(\boldsymbol{r} = \left( { – \frac{1}{{12}}\boldsymbol{i} – \frac{1}{6}\boldsymbol{j}} \right) + \lambda \left( { – \frac{1}{6}\boldsymbol{i} + \frac{2}{3}\boldsymbol{j} + \boldsymbol{k}} \right)\) A1A1A1 N3
[6 marks]
METHOD 2
(Elimination method either for equations or row reduction of matrix)
Eliminating one of the variables M1A1
Finding a point on the line (M1)A1
Finding the direction of the line M1
The vector equation of the line A1 N3
[6 marks]
Examiners report
A large number of candidates did not use their GDC in this question. Some candidates who attempted analytical solutions looked for a point solution although the question specifically states that the planes intersect in a line. Other candidates eliminated one variable and then had no clear strategy for proceeding with the solution.
Some candidates failed to write ‘r =’, and others did not give the equation in vector form.
Question
(a) Write the vector equations of the following lines in parametric form.
\[{r_1} = \left( {\begin{array}{*{20}{c}}
3 \\
2 \\
7
\end{array}} \right) + m\left( {\begin{array}{*{20}{c}}
2 \\
{ – 1} \\
2
\end{array}} \right)\]
\[{r_2} = \left( {\begin{array}{*{20}{c}}
1 \\
4 \\
2
\end{array}} \right) + n\left( {\begin{array}{*{20}{c}}
4 \\
{ – 1} \\
1
\end{array}} \right)\]
(b) Hence show that these two lines intersect and find the point of intersection, A.
(c) Find the Cartesian equation of the plane \(\prod \) that contains these two lines.
(d) Let B be the point of intersection of the plane \(\prod \) and the line\({r} = \left( {\begin{array}{*{20}{c}}
{ – 8} \\
{ – 3} \\
0
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}
3 \\
8 \\
2
\end{array}} \right)\).
Find the coordinates of B.
(e) If C is the mid-point of AB, find the vector equation of the line perpendicular to the plane \(\prod \) and passing through C.
Answer/Explanation
Markscheme
(a) \(x = 3 + 2m\)
\(y = 2 – m\)
\(z = 7 + 2m\) A1
\(x = 1 + 4n\)
\(y = 4 – n\)
\(z = 2 + n\) A1
[2 marks]
(b) \(3 + 2m = 1 + 4n \Rightarrow 2m – 4n = – 2{\text{ }}({\text{i}})\)
\(2 – m = 4 – n \Rightarrow m – n = – 2{\text{ }}({\text{ii}})\) M1
\(7 + 2m = 2 + n \Rightarrow 2m – n = – 5{\text{ }}({\text{iii}})\)
\(({\text{iii}}) – ({\text{ii}}) \Rightarrow m = – 3\) A1
\( \Rightarrow n = – 1\) A1
Substitute in (i), –6 + 4 = –2 . Hence lines intersect. R1
Point of intersection A is (–3, 5,1) A1
[5 marks]
(c) \(\left| {\begin{array}{*{20}{c}}
i&j&k \\
2&{ – 1}&2 \\
4&{ – 1}&1
\end{array}} \right| = \left( {\begin{array}{*{20}{c}}
1 \\
6 \\
2
\end{array}} \right)\) M1A1
\(r \cdot \left( {\begin{array}{*{20}{c}}
1 \\
6 \\
2
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
3 \\
2 \\
7
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
1 \\
6 \\
2
\end{array}} \right)\) (M1)
\(r \cdot \left( {\begin{array}{*{20}{c}}
1 \\
6 \\
2
\end{array}} \right) = 29\)
x + 6y + 2z = 29 A1
Note: Award M1A0 if answer is not in Cartesian form.
[4 marks]
(d) \(x = – 8 + 3\lambda \)
\(y = – 3 + 8\lambda \) (M1)
\(z = 2\lambda \)
Substitute in equation of plane.
\( – 8 + 3\lambda – 18 + 48\lambda + 4\lambda = 29\) M1
\(55\lambda = 55\)
\(\lambda = 1\) A1
Coordinates of B are (–5, 5, 2) A1
[4 marks]
(e) Coordinates of C are \(\left( { – 4,{\text{ 5, }}\frac{3}{2}} \right)\) (A1)
\(r = \left( {\begin{array}{*{20}{c}}
{ – 4} \\
5 \\
{\frac{3}{2}}
\end{array}} \right) + \mu \left( {\begin{array}{*{20}{c}}
1 \\
6 \\
2
\end{array}} \right)\) M1A1
Note: Award M1A0 unless candidate writes r = or \(\left( {\begin{array}{*{20}{c}}
x \\
y \\
z
\end{array}} \right)\)
[3 marks]
Total [18 marks]
Examiners report
Most candidates found this question to their liking and many correct solutions were seen. In (b), some candidates solved two equations for m and n but then failed to show that these values satisfied the third equation. In (e), some candidates used an incorrect formula to determine the coordinates of the mid-point of AB .
Question
(a) If \(a = 4\) find the coordinates of the point of intersection of the three planes.
(b) (i) Find the value of \(a\) for which the planes do not meet at a unique point.
(ii) For this value of \(a\) show that the three planes do not have any common point.
Answer/Explanation
Markscheme
(a) let \({\boldsymbol{A}} = \left( {\begin{array}{*{20}{c}}
1&1&2 \\
2&{ – 1}&3 \\
5&{ – 1}&4
\end{array}} \right)\) , \({\boldsymbol{X}} = \left( {\begin{array}{*{20}{c}}
x \\
y \\
z
\end{array}} \right)\) , and \({\boldsymbol{B}} = \left( {\begin{array}{*{20}{c}}
2 \\
2 \\
5
\end{array}} \right)\) (M1)
point of intersection is \(\left( {\frac{{11}}{{12}},\frac{7}{{12}},\frac{1}{4}} \right)\) or \(\left( {{\text{or }}\left( {{\text{0}}{\text{.917, 0}}{\text{.583, 0}}{\text{.25}}} \right)} \right)\) A1
(b) METHOD 1
(i) \(\det \left( {\begin{array}{*{20}{c}}
1&1&2 \\
2&{ – 1}&3 \\
5&{ – 1}&4
\end{array}} \right) = 0\) M1
\( – 3a + 24 = 0\) (A1)
\(a = 8\) A1 N1
(ii) consider the augmented matrix \(\left( {\begin{array}{*{20}{ccc|c}}
1&1&2&2 \\
2&{ – 1}&3&2 \\
5&{ – 1}&4&5
\end{array}} \right)\) M1
use row reduction to obtain \(\left( {\begin{array}{*{20}{ccc|c}}
1&1&2&2 \\
0&{ – 3}&{ – 1}&{ – 2} \\
0&0&0&{ – 1}
\end{array}} \right)\) or \(\left( {\begin{array}{*{20}{ccc|c}}
1&0&{\frac{5}{3}}&0 \\
0&1&{\frac{1}{3}}&0 \\
0&0&0&1
\end{array}} \right)\) (or equivalent) A1
any valid reason R1
(e.g. as the last row is not all zeros, the planes do not meet) N0
METHOD 2
use of row reduction (or equivalent manipulation of equations) M1
e.g. \(\left( {\begin{array}{*{20}{c}}
1&1&2&2 \\
2&{ – 1}&3&2 \\
5&{ – 1}&a&5
\end{array}} \right) \Rightarrow \left( {\begin{array}{*{20}{c}}
1&1&2&2 \\
0&{ – 3}&{ – 1}&{ – 2} \\
0&{ – 6}&{a – 10}&{ – 5}
\end{array}} \right)\) A1A1
Note: Award an A1 for each correctly reduced row.
(i) \(a -10 = -2 \Rightarrow a = 8\) M1A1 N1
(ii) when \(a = 8\) , row 3 \( \ne \) 2 \( \times \) row 2 R1 N0
[8 marks]
Examiners report
Few students were able to do this question efficiently. Many students were able to do part (a) by manipulating equations, whereas calculator methods would yield the solution quickly and easily. Part (b) was poorly attempted and it was apparent that many students used a lot of time manipulating equations without real understanding of what they were looking for.
Question
The diagram shows a cube OABCDEFG.
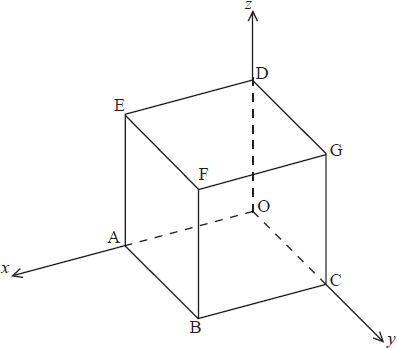
Let O be the origin, (OA) the x-axis, (OC) the y-axis and (OD) the z-axis.
Let M, N and P be the midpoints of [FG], [DG] and [CG], respectively.
The coordinates of F are (2, 2, 2).
(a) Find the position vectors \(\overrightarrow {{\text{OM}}} \), \(\overrightarrow {{\text{ON}}} \) and \(\overrightarrow {{\text{OP}}} \) in component form.
(b) Find \(\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} \).
(c) Hence,
(i) calculate the area of the triangle MNP;
(ii) show that the line (AG) is perpendicular to the plane MNP;
(iii) find the equation of the plane MNP.
(d) Determine the coordinates of the point where the line (AG) meets the plane MNP.
Answer/Explanation
Markscheme
(a) \(\overrightarrow {{\text{OM}}} = \left( {\begin{array}{*{20}{c}}
1 \\
2 \\
2
\end{array}} \right)\), \(\overrightarrow {{\text{ON}}} = \left( {\begin{array}{*{20}{c}}
0 \\
1 \\
2
\end{array}} \right)\) and \(\overrightarrow {{\text{OP}}} = \left( {\begin{array}{*{20}{c}}
0 \\
2 \\
1
\end{array}} \right)\) A1A1A1
[3 marks]
(b) \(\overrightarrow {{\text{MP}}} = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
0 \\
{ – 1}
\end{array}} \right)\) and \(\overrightarrow {{\text{MN}}} = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
{ – 1} \\
0
\end{array}} \right)\) A1A1
\(\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} = \left( {\begin{array}{*{20}{c}}
i&j&k \\
{ – 1}&0&{ – 1} \\
{ – 1}&{ – 1}&0
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right)\) (M1)A1
[4 marks]
(c) (i) area of MNP \( = \frac{1}{2}\left| {\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} } \right|\) M1
\( = \frac{1}{2}\left| {\left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right)} \right|\)
\( = \frac{{\sqrt 3 }}{2}\) A1
(ii) \(\overrightarrow {{\text{OA}}} = \left( {\begin{array}{*{20}{c}}
2 \\
0 \\
0
\end{array}} \right)\), \(\overrightarrow {{\text{OG}}} = \left( {\begin{array}{*{20}{c}}
0 \\
2 \\
2
\end{array}} \right)\)
\(\overrightarrow {{\text{AG}}} = \left( {\begin{array}{*{20}{c}}
{ – 2} \\
2 \\
2
\end{array}} \right)\) A1
since \(\overrightarrow {{\text{AG}}} = 2(\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} )\) AG is perpendicular to MNP R1
(iii) \(r \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1 \\
2 \\
2
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right)\) M1A1
\(r \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right) = 3\) (accept \( – x + y + z = 3\)) A1
[7 marks]
(d) \(r = \left( {\begin{array}{*{20}{c}}
2 \\
0 \\
0
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}
{ – 2} \\
2 \\
2
\end{array}} \right)\) A1
\(\left( {\begin{array}{*{20}{c}}
{2 – 2\lambda } \\
{2\lambda } \\
{2\lambda }
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right) = 3\) M1A1
\( – 2 + 2\lambda + 2\lambda + 2\lambda = 3\)
\(\lambda = \frac{5}{6}\) A1
\(r = \left( {\begin{array}{*{20}{c}}
2 \\
0 \\
0
\end{array}} \right) + \frac{5}{6}\left( {\begin{array}{*{20}{c}}
{ – 2} \\
2 \\
2
\end{array}} \right)\) M1
coordinates of point \(\left( {\frac{1}{3},\frac{5}{3},\frac{5}{3}} \right)\) A1
[6 marks]
Total [20 marks]
Examiners report
This was the most successfully answered question in part B, with many candidates achieving full marks. There were a few candidates who misread the question and treated the cube as a unit cube. The most common errors were either algebraic or arithmetic mistakes. A variety of notation forms were seen but in general were used consistently. In a few cases, candidates failed to show all the work or set it properly.
Question
Two planes \({\Pi _1}\) and \({\Pi _2}\) have equations \(2x + y + z = 1\) and \(3x + y – z = 2\) respectively.
Find the vector equation of L, the line of intersection of \({\Pi _1}\) and \({\Pi _2}\).
Show that the plane \({\Pi _3}\) which is perpendicular to \({\Pi _1}\) and contains L, has equation \(x – 2z = 1\).
The point P has coordinates (−2, 4, 1) , the point Q lies on \({\Pi _3}\) and PQ is perpendicular to \({\Pi _2}\). Find the coordinates of Q.
Answer/Explanation
Markscheme
(a) METHOD 1
solving simultaneously (gdc) (M1)
\(x = 1 + 2z;{\text{ }}y = – 1 – 5z\) A1A1
\(L:\boldsymbol{r} = \left( {\begin{array}{*{20}{c}}
1 \\
{ – 1} \\
0
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}
2 \\
{ – 5} \\
1
\end{array}} \right)\) A1A1A1
Note: \({1^{{\text{st}}}}\) A1 is for r =.
[6 marks]
METHOD 2
direction of line \( = \left| {\begin{array}{*{20}{c}}
\boldsymbol{i}&\boldsymbol{j}&\boldsymbol{k} \\
3&1&{ – 1} \\
2&1&1
\end{array}} \right|\) (last two rows swapped) M1
= 2i − 5j + k A1
putting z = 0, a point on the line satisfies \(2x + y = 1,{\text{ }}3x + y = 2\) M1
i.e. (1, −1, 0) A1
the equation of the line is
\(\left( {\begin{array}{*{20}{c}}
x \\
y \\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1 \\
{ – 1} \\
0
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}
2 \\
{ – 5} \\
1
\end{array}} \right)\) A1A1
Note: Award A0A1 if \(\left( {\begin{array}{*{20}{c}}
x \\
y \\
z
\end{array}} \right)\) is missing.
[6 marks]
\(\left( {\begin{array}{*{20}{c}}
2 \\
1 \\
1
\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}
2 \\
{ – 5} \\
1
\end{array}} \right)\) M1
= 6i − 12k A1
hence, n = i − 2k
\({\boldsymbol{n}} \cdot {\boldsymbol{a}} = \left( {\begin{array}{*{20}{c}}
1 \\
0 \\
{ – 2}
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
1 \\
{ – 1} \\
0
\end{array}} \right) = 1\) M1A1
therefore r \( \cdot \) n = a \( \cdot \) n \( \Rightarrow x – 2z = 1\) AG
[4 marks]
METHOD 1
P = (−2, 4, 1), Q = \((x,{\text{ }}y,{\text{ }}z)\)
\(\overrightarrow {{\text{PQ}}} = \left( {\begin{array}{*{20}{c}}
{x + 2} \\
{y – 4} \\
{z – 1}
\end{array}} \right)\) A1
\(\overrightarrow {{\text{PQ}}} \) is perpendicular to \(3x + y – z = 2\)
\( \Rightarrow \overrightarrow {{\text{PQ}}} \) is parallel to 3i + j − k R1
\( \Rightarrow x + 2 = 3t;{\text{ }}y – 4 = t;{\text{ }}z – 1 = – t\) A1
\(1 – z = t \Rightarrow x + 2 = 3 – 3z \Rightarrow x + 3z = 1\) A1
solving simultaneously \(x + 3z = 1;{\text{ }}x – 2z = 1\) M1
\(5z = 0 \Rightarrow z = 0;{\text{ }}x = 1,{\text{ }}y = 5\) A1
hence, Q = (1, 5, 0)
[6 marks]
METHOD 2
Line passing through PQ has equation
\({\mathbf{r}} = \begin{array}{*{20}{c}}
{ – 2} \\
4 \\
1
\end{array} + t\begin{array}{*{20}{c}}
3 \\
1 \\
{ – 1}
\end{array}\) M1A1
Meets \({\pi _3}\) when:
\( – 2 + 3t – 2(1 – t) = 1\) M1A1
t = 1 A1
Q has coordinates (1, 5, 0) A1
[6 marks]
Examiners report
Candidates generally attempted this question but with varying degrees of success. Although (a) was answered best of all the parts, quite a few did not use correct notation to designate the vector equation of a line, i.e., r =, or its equivalent. In (b) some candidates incorrectly assumed the result and worked the question from there. In (c) some candidates did not understand the necessary relationships to make a meaningful attempt.
Candidates generally attempted this question but with varying degrees of success. Although (a) was answered best of all the parts, quite a few did not use correct notation to designate the vector equation of a line, i.e., r =, or its equivalent. In (b) some candidates incorrectly assumed the result and worked the question from there. In (c) some candidates did not understand the necessary relationships to make a meaningful attempt.
Candidates generally attempted this question but with varying degrees of success. Although (a) was answered best of all the parts, quite a few did not use correct notation to designate the vector equation of a line, i.e., r =, or its equivalent. In (b) some candidates incorrectly assumed the result and worked the question from there. In (c) some candidates did not understand the necessary relationships to make a meaningful attempt.
Question
The planes \(2x + 3y – z = 5\) and \(x – y + 2z = k\) intersect in the line \(5x + 1 = 9 – 5y = – 5z\) .
Find the value of k .
Answer/Explanation
Markscheme
point on line is \(x = \frac{{ – 1 – 5\lambda }}{5}{\text{, }}y = \frac{{9 + 5\lambda }}{5}{\text{, }}z = \lambda \) or similar M1A1
Note: Accept use of point on the line or elimination of one of the variables using the equations of the planes
\(\frac{{ – 1 – 5\lambda }}{5} – \frac{{9 + 5\lambda }}{5} + 2\lambda = k\) M1A1
Note: Award M1A1 if coordinates of point and equation of a plane is used to obtain linear equation in k or equations of the line are used in combination with equation obtained by elimination to get linear equation in k.
\(k = – 2\) A1
[5 marks]
Examiners report
Many different attempts were seen, sometimes with success. Unfortunately many candidates wasted time with aimless substitutions showing little understanding of the problem.
Question
Find the values of k for which the following system of equations has no solutions and the value of k for the system to have an infinite number of solutions.
\[x – 3y + z = 3\]
\[x + 5y – 2z = 1\]
\[16y – 6z = k\]
Given that the system of equations can be solved, find the solutions in the form of a vector equation of a line, r = a + λb , where the components of b are integers.
The plane \( \div \) is parallel to both the line in part (b) and the line \(\frac{{x – 4}}{3} = \frac{{y – 6}}{{ – 2}} = \frac{{z – 2}}{0}\).
Given that \( \div \) contains the point (1, 2, 0) , show that the Cartesian equation of ÷ is 16x + 24y − 11z = 64 .
The z-axis meets the plane \( \div \) at the point P. Find the coordinates of P.
Find the angle between the line \(\frac{{x – 2}}{3} = \frac{{y + 5}}{4} = \frac{z}{2}\) and the plane \( \div \) .
Answer/Explanation
Markscheme
in augmented matrix form \(\left| {\begin{array}{*{20}{c}}
1&{ – 3}&1&3 \\
1&5&{ – 2}&1 \\
0&{16}&{ – 6}&k
\end{array}} \right|\)
attempt to find a line of zeros (M1)
\({r_2} – {r_1}\left| {\begin{array}{*{20}{c}}
1&{ – 3}&1&3 \\
0&8&{ – 3}&{ – 2} \\
0&{16}&{ – 6}&k
\end{array}} \right|\) (A1)
\({r_3} – 2{r_2}\left| {\begin{array}{*{20}{c}}
1&{ – 3}&1&3 \\
0&8&{ – 3}&{ – 2} \\
0&{0}&{0}&{k + 4}
\end{array}} \right|\) (A1)
there is an infinite number of solutions when \(k = – 4\) R1
there is no solution when
\(k \ne – 4,{\text{ }}(k \in \mathbb{R})\) R1
Note: Approaches other than using the augmented matrix are acceptable.
[5 marks]
using \(\left| {\begin{array}{*{20}{c}}
1&{ – 3}&1&3 \\
0&8&{ – 3}&{ – 2} \\
0&{0}&{ 0}&{k + 4}
\end{array}} \right|\) and letting \(\boldsymbol{z} = \lambda \) (M1)
\(8y – 3\lambda = – 2\)
\( \Rightarrow y = \frac{{3\lambda – 2}}{8}\) (A1)
\(x – 3y + z = 3\)
\( \Rightarrow x – \left( {\frac{{9\lambda – 6}}{8}} \right) + \lambda = 3\) (M1)
\( \Rightarrow 8x – 9\lambda + 6 + 8\lambda = 24\)
\( \Rightarrow x = \frac{{18 + \lambda }}{8}\) (A1)
\( \Rightarrow \left( {\begin{array}{*{20}{c}}
x \\
y \\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{\frac{{18}}{8}} \\
{ – \frac{2}{8}} \\
0
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}
{\frac{1}{8}} \\
{\frac{3}{8}} \\
1
\end{array}} \right)\) (M1)(A1)
\(r = \left( {\begin{array}{*{20}{c}}
{\frac{9}{4}} \\
{ – \frac{1}{4}} \\
0
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}
1 \\
3 \\
8
\end{array}} \right)\) A1
Note: Accept equivalent answers.
[7 marks]
recognition that \(\left( {\begin{array}{*{20}{c}}
3 \\
{ – 2} \\
0
\end{array}} \right)\) is parallel to the plane (A1)
direction normal of the plane is given by \(\left| {\begin{array}{*{20}{c}}
\boldsymbol{i}&\boldsymbol{j}&\boldsymbol{k} \\
1&3&8 \\
3&{ – 2}&0
\end{array}} \right|\) (M1)
= 16i + 24j – 11k A1
Cartesian equation of the plane is given by 16x + 24y –11z = d and a point which fits this equation is (1, 2, 0) (M1)
\( \Rightarrow 16 + 48 = d\)
d = 64 A1
hence Cartesian equation of plane is 16x + 24y –11z = 64 AG
Note: Accept alternative methods using dot product.
[5 marks]
the plane crosses the z-axis when x = y = 0 (M1)
coordinates of P are \(\left( {0,\,0,\, – \frac{{64}}{{11}}} \right)\) A1
Note: Award A1 for stating \(z = – \frac{{64}}{{11}}\).
Note: Accept. \(\left( {\begin{array}{*{20}{c}}
0 \\
0 \\
{ – \frac{{64}}{{11}}}
\end{array}} \right)\)
[2 marks]
recognition that the angle between the line and the direction normal is given by:
\(\left( {\begin{array}{*{20}{c}}
3 \\
4 \\
2
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{16} \\
{24} \\
{-11}
\end{array}} \right) = \sqrt {29} \sqrt {953} \cos \theta \) where \(\theta \) is the angle between the line and the normal vector M1A1
\( \Rightarrow 122 = \sqrt {29} \sqrt {953} \cos \theta \) (A1)
\( \Rightarrow \theta = 42.8^\circ {\text{ (0.747 radians)}}\) (A1)
hence the angle between the line and the plane is 90° – 42.8° = 47.2° (0.824 radians) A1
[5 marks]
Note: Accept use of the formula a.b = \(\left| {} \right.\)a\(\left. {} \right|\)\(\left| {} \right.\)b\(\left| {\sin \theta } \right.\) .
Examiners report
Many candidates were able to start this question, but only a few candidates gained full marks. Many candidates successfully used the augmented matrix in part (a) to find the correct answer. Part (b) was less successful with only a limited number of candidates using the calculator to its full effect here and with many candidates making arithmetic and algebraic errors. This was the hardest part of the question. Many candidates understood the vector techniques necessary to answer parts (c), (d) and (e) but a number made arithmetic and algebraic errors in the working.
Many candidates were able to start this question, but only a few candidates gained full marks. Many candidates successfully used the augmented matrix in part (a) to find the correct answer. Part (b) was less successful with only a limited number of candidates using the calculator to its full effect here and with many candidates making arithmetic and algebraic errors. This was the hardest part of the question. Many candidates understood the vector techniques necessary to answer parts (c), (d) and (e) but a number made arithmetic and algebraic errors in the working.
Many candidates were able to start this question, but only a few candidates gained full marks. Many candidates successfully used the augmented matrix in part (a) to find the correct answer. Part (b) was less successful with only a limited number of candidates using the calculator to its full effect here and with many candidates making arithmetic and algebraic errors. This was the hardest part of the question. Many candidates understood the vector techniques necessary to answer parts (c), (d) and (e) but a number made arithmetic and algebraic errors in the working.
Many candidates were able to start this question, but only a few candidates gained full marks. Many candidates successfully used the augmented matrix in part (a) to find the correct answer. Part (b) was less successful with only a limited number of candidates using the calculator to its full effect here and with many candidates making arithmetic and algebraic errors. This was the hardest part of the question. Many candidates understood the vector techniques necessary to answer parts (c), (d) and (e) but a number made arithmetic and algebraic errors in the working.
Many candidates were able to start this question, but only a few candidates gained full marks. Many candidates successfully used the augmented matrix in part (a) to find the correct answer. Part (b) was less successful with only a limited number of candidates using the calculator to its full effect here and with many candidates making arithmetic and algebraic errors. This was the hardest part of the question. Many candidates understood the vector techniques necessary to answer parts (c), (d) and (e) but a number made arithmetic and algebraic errors in the working.
Question
The lines \({l_1}\) and \({l_2}\) are defined as
\({l_1}:\frac{{x – 1}}{3} = \frac{{y – 5}}{2} = \frac{{z – 12}}{{ – 2}}\)
\({l_2}:\frac{{x – 1}}{8} = \frac{{y – 5}}{{11}} = \frac{{z – 12}}{6}\).
The plane \(\pi \) contains both \({l_1}\) and \({l_2}\).
Find the Cartesian equation of \(\pi \).
The line \({l_3}\) passing through the point \((4,{\text{ }}0,{\text{ }}8)\) is perpendicular to \(\pi \).
Find the coordinates of the point where \({l_3}\) meets \(\pi \).
Answer/Explanation
Markscheme
attempting to find a normal to \(\pi {\text{ }}eg{\text{ }}\left( {\begin{array}{*{20}{c}} 3 \\ 2 \\ { – 2} \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} 8 \\ {11} \\ 6 \end{array}} \right)\) (M1)
\(\left( {\begin{array}{*{20}{c}} 3 \\ 2 \\ { – 2} \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} 8 \\ {11} \\ 6 \end{array}} \right) = 17\left( {\begin{array}{*{20}{c}} 2 \\ { – 2} \\ 1 \end{array}} \right)\) (A1)
\({{r}} \bullet \left( {\begin{array}{*{20}{c}} 2 \\ { – 2} \\ 1 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1 \\ 5 \\ {12} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} 2 \\ { – 2} \\ 1 \end{array}} \right)\) M1
\(2x – 2y + z = 4\) (or equivalent) A1
[4 marks]
\({l_3}:{{r}} = \left( {\begin{array}{*{20}{c}} 4 \\ 0 \\ 8 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 2 \\ { – 2} \\ 1 \end{array}} \right),\;\;\;t \in \mathbb{R}\) (A1)
attempting to solve \(\left( {\begin{array}{*{20}{c}} {4 + 2t} \\ { – 2t} \\ {8 + t} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} 2 \\ { – 2} \\ 1 \end{array}} \right) = 4\;\;\;{\text{for }}t\;\;\;ie{\text{ }}9t + 16 = 4\;\;\;{\text{for }}t\) M1
\(t = – \frac{4}{3}\) A1
\(\left( {\frac{4}{3},{\text{ }}\frac{8}{3},{\text{ }}\frac{{20}}{3}} \right)\) A1
[4 marks]
Total [8 marks]
Examiners report
Part (a) was reasonably well done. Some candidates made numerical errors when attempting to find a normal to \(\pi \).
In part (b), a number of candidates were awarded follow through marks from numerical errors committed in part (a).

