Question: [Maximum mark: 6]
Let A and B be two independent events such that P(A ∩ B′) = 0.16 and P(A′ ∩ B) = 0.36.
(a) Given that P(A ∩ B) = x , find the value of x .
(b) Find P(A′ | B′).
▶️Answer/Explanation
Ans:
(a) METHOD 1
EITHER
one of P(A) = x + 0.16 OR P(B) = x + 0.36
OR
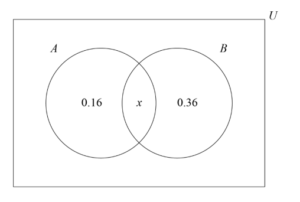
THEN
attempt to equate their P(A ∩ B ) with their expression for P (A) × P(B)
P(A ∩ B ) = P (A) × P(B) ⇒x=(x+0.16) ×(x+0.36)
x = 0.24
METHOD 2
attempt to form at least one equation in P(A) and P(B) using independence
(P(A ∩ B’ ) = P (A) × P(B’) ⇒) P(A) × (1-P(B)) = 0.16 OR
(P(A’ ∩ B ) = P (A’) × P(B) ⇒) (1-P(A)) × P(B) = 0.36
P(A) = 0.4 And P(B) = 0.6
P(A ∩ B ) = P (A) × P(B) = 0.4 × 0.6
x = 0.24
(b) METHOD 1
recognising P(A’|B’) = P(A)
= 1- 0.16 – 0.24
= 0.6
METHOD 2
P(B) = 0.36 + 0.24 (=0.6)
\(P(A’|B’)=\frac{P(A’\bigcap B’)}{P(B’)}\left ( =\frac{0.24}{0.4} \right )\)
=0.6
Question
At a school, 70 % of the students play a sport and 20 % of the students are involved in theatre. 18 % of the students do neither activity.
A student is selected at random.
(a) Find the probability that the student plays a sport and is involved in theatre. [2]
(b) Find the probability that the student is involved in theatre, but does not play a sport. [2]
At the school 48 % of the students are girls, and 25 % of the girls are involved in theatre.
A student is selected at random. Let G be the event “the student is a girl” and let T be the event “the student is involved in theatre”.
(c) Find P (G ∩ T ) . [2]
(d) Determine if the events G and T are independent. Justify your answer. [2]
▶️Answer/Explanation
Ans:
(a) By using the combined events formula, we have $\begin{eqnarray} \text{P}\left(S\cup T\right) = \text{P}\left(S\right)+\text{P}\left(T\right)-\text{P}\left(S\cap T\right) \nonumber \\ 0.82 = 0.7+0.2-\text{P}\left(S\cap T\right) \nonumber \\ \text{P}\left(S\cap T\right) = 0.08. \end{eqnarray}$ (b) $\begin{eqnarray} \text{P}\left(T\cap S’\right) &=& \text{P}\left(t\right)-\text{P}\left(S\cap T\right) \nonumber \\ &=& 0.2-0.08 \nonumber \\ &=& 0.12. \end{eqnarray}$ (c) $\begin{eqnarray} \text{P}\left(G\cap T\right) &=& 0.48\times 0.25 \nonumber \\ &=& 0.12. \end{eqnarray}$ (d) Since $\begin{eqnarray} \text{P}\left(G\right)\times\text{P}\left(T\right) &=& 0.48\times 0.2 \nonumber \\ &=& 0.096 \nonumber \\ &\neq & 0.12 \nonumber \\ &=& \text{P}\left(G\cap T\right), \end{eqnarray}$ $G$ and $T$ are not independent.
Question
Ava and Barry play a game with a bag containing one green marble and two red marbles. Each player in turn randomly selects a marble from the bag, notes its colour and replaces it. Ava wins the game if she selects a green marble. Barry wins the game if he selects a red marble. Ava starts the game.
a.Find the probability that Ava wins on her first turn.[1]
b.Find the probability that Barry wins on his first turn.[2]
c.Find the probability that Ava wins in one of her first three turns.[4]
d.Find the probability that Ava eventually wins.[4]
▶️Answer/Explanation
Markscheme
\({\text{P(Ava wins on her first turn)}} = \frac{1}{3}\) A1
[1 mark]
\({\text{P(Barry wins on his first turn)}} = {\left( {\frac{2}{3}} \right)^2}\) (M1)
\( = \frac{4}{9}\;\;\;( = 0.444)\) A1
[2 marks]
\(P\)(Ava wins in one of her first three turns)
\( = \frac{1}{3} + \left( {\frac{2}{3}} \right)\left( {\frac{1}{3}} \right)\frac{1}{3} + \left( {\frac{2}{3}} \right)\left( {\frac{1}{3}} \right)\left( {\frac{2}{3}} \right)\left( {\frac{1}{3}} \right)\frac{1}{3}\) M1A1A1
Note: Award M1 for adding probabilities, award A1 for a correct second term and award A1 for a correct third term.
Accept a correctly labelled tree diagram, awarding marks as above.
\( = \frac{{103}}{{243}}\;\;\;( = 0.424)\) A1
[4 marks]
\({\text{P(Ava eventually wins)}} = \frac{1}{3} + \left( {\frac{2}{3}} \right)\left( {\frac{1}{3}} \right)\frac{1}{3} + \left( {\frac{2}{3}} \right)\left( {\frac{1}{3}} \right)\left( {\frac{2}{3}} \right)\left( {\frac{1}{3}} \right)\frac{1}{3} + \ldots \) (A1)
using \({S_\infty } = \frac{a}{{1 – r}}\) with \(a = \frac{1}{3}\) and \(r = \frac{2}{9}\) (M1)(A1)
Note: Award (M1) for using \({S_\infty } = \frac{a}{{1 – r}}\) and award (A1) for \(a = \frac{1}{3}\) and \(r = \frac{2}{9}\).
\( = \frac{3}{7}\;\;\;( = 0.429)\) A1
[4 marks]
Total [11 marks]
Question
The events \(A\) and \(B\) are such that \({\text{P}}(A) = 0.65\), \({\text{P}}(B) = 0.48\) and \({\text{P}}(A \cup B) = 0.818\).
a.Find \({\text{P}}(A \cap B)\).[2]
b.Hence show that the events \(A\) and \(B\) are independent.[2]
▶️Answer/Explanation
Markscheme
Note: In Section A, where appropriate, accept answers that correctly round to 2 sf except in Q2, Q5(a) (ii), Q5(b) and Q8(a).
\(0.818 = 0.65 + 0.48 – {\text{P}}(A \cap B)\) (M1)
\({\text{P}}(A \cap B) = 0.312\) A1
[2 marks]
\({\text{P}}(A)P(B) = 0.312\;\;\;( = 0.48 \times 0.65)\) A1
since \({\text{P}}(A)P(B) = {\text{P}}(A \cap B)\) then \(A\) and \(B\) are independent R1
Note: Only award the R1 if numerical values are seen. Award A1R1 for a correct conditional probability approach.
[2 marks]
Total [4 marks]
