Download IITian Academy App for accessing Online Mock Tests and More..
Question
The following table shows the average weights ( y kg) for given heights (x cm) in a population of men.
| Heights (x cm) | 165 | 170 | 175 | 180 | 185 |
| Weights (y kg) | 67.8 | 70.0 | 72.7 | 75.5 | 77.2 |
The relationship between the variables is modelled by the regression equation \(y = ax + b\).
Write down the value of \(a\) and of \(b\).
The relationship between the variables is modelled by the regression equation \(y = ax + b\).
Hence, estimate the weight of a man whose height is 172 cm.
Write down the correlation coefficient.
State which two of the following describe the correlation between the variables.
| strong | zero | positive |
| negative | no correlation | weak |
Answer/Explanation
Markscheme
\(a = 0.486\) (exact) A1 N1
\(b = – 12.41\) (exact), \(-12.4\) A1 N1
[2 marks]
correct substitution (A1)
eg \(0.486(172) – 12.41\)
\(71.182\)
\(71.2\) (kg) A1 N2
[2 marks]
\(r = 0.997276\)
\(r = 0.997\) A1 N1
[1 mark]
strong, positive (must have both correct) A2 N2
[2 marks]
Question
The following table shows the amount of fuel (\(y\) litres) used by a car to travel certain distances (\(x\) km).
| Distance (x km) | 40 | 75 | 120 | 150 | 195 |
| Amount of fuel (y litres) | 3.6 | 6.5 | 9.9 | 13.1 | 16.2 |
This data can be modelled by the regression line with equation \(y = ax + b\).
Write down the value of \(a\) and of \(b\).
Explain what the gradient \(a\) represents.
Use the model to estimate the amount of fuel the car would use if it is driven \(110\) km.
Answer/Explanation
Markscheme
\(a = 0.0823604{\text{, }}b = 0.306186\)
\(a = 0.0824{\text{, }}b = 0.306\) A1A1 N2
[2 marks]
correct explanation with reference to number of litres
required for \(1\) km A1 N1
eg \(a\) represents the (average) amount of fuel (litres) required to drive \(1\) km, (average) litres per kilometre, (average) rate of change in fuel used for each km travelled
[1 marks]
valid approach (M1)
eg \(y = 0.0824(110) + 0.306\), sketch
\(9.36583\)
\(9.37\) (litres) A1 N2
[2 marks]
Question
The following table shows the Diploma score \(x\) and university entrance mark \(y\) for seven IB Diploma students.
Find the correlation coefficient.
The relationship can be modelled by the regression line with equation \(y = ax + b\).
Write down the value of \(a\) and of \(b\).
Rita scored a total of \(26\) in her IB Diploma.
Use your regression line to estimate Rita’s university entrance mark.
Answer/Explanation
Markscheme
evidence of set up (M1)
eg\(\;\;\;\)correct value for \(r\) (or for \(a\) or \(r\), seen in (b))
\(0.996010\)
\(r = 0.996\;\;\;[0.996,{\text{ }}0.997]\) A1 N2
[2 marks]
\(a = 3.15037,{\text{ }}b = – 15.4393\)
\(a = 3.15{\text{ }}[3.15,{\text{ }}3.16],{\text{ }}b = – 15.4{\text{ }}[ – 15.5,{\text{ }} – 15.4]\) A1A1 N2
[2 marks]
substituting \(26\) into their equation (M1)
eg\(\;\;\;\)\(y = 3.15(26) – 15.4\)
\(66.4704\)
\(66.5{\text{ }}[66.4,{\text{ }}66.5]\) A1 N2
[2 marks]
Total [6 marks]
Question
The following table shows the average number of hours per day spent watching television by seven mothers and each mother’s youngest child.
The relationship can be modelled by the regression line with equation \(y = ax + b\).
(i) Find the correlation coefficient.
(ii) Write down the value of \(a\) and of \(b\).
Elizabeth watches television for an average of \(3.7\) hours per day.
Use your regression line to predict the average number of hours of television watched per day by Elizabeth’s youngest child. Give your answer correct to one decimal place.
Answer/Explanation
Markscheme
(i) evidence of valid approach (M1)
eg\(\;\;\;\)\(1\) correct value for \(r\), (or for \(a\) or \(b\), seen in (ii))
\(0.946591\)
\(r = 0.947\) A1 N2
(ii) \(a = 0.500957,{\text{ }}b = 0.803544\)
\(a = 0.501,{\text{ }}b = 0.804\) A1A1 N2
[4 marks]
substituting \(x = 3.7\) into their equation (M1)
eg\(\;\;\;0.501(3.7) + 0.804\)
\(2.65708\;\;\;\)(\(2\) hours \(39.4252\) minutes) (A1)
\(y = 2.7\) (hours) (must be correct \(1\) dp, accept \(2\) hours \(39.4\) minutes) A1 N3
[3 marks]
Total [7 marks]
Question
The following table shows the sales, \(y\) millions of dollars, of a company, \(x\) years after it opened.
The relationship between the variables is modelled by the regression line with equation \(y = ax + b\).
(i) Find the value of \(a\) and of \(b\).
(ii) Write down the value of \(r\).
Hence estimate the sales in millions of dollars after seven years.
Answer/Explanation
Markscheme
(i) evidence of set up (M1)
eg\(\;\;\;\)correct value for \(a\), \(b\) or \(r\)
\(a = 4.8,{\text{ }}b = 1.2\) A1A1 N3
(ii) \(r = 0.988064\)
\(r = 0.988\) A1 N1
[4 marks]
correct substitution into their regression equation (A1)
eg\(\;\;\;4.8 \times 7 + 1.2\)
\(34.8\) (millions of dollars) (accept \(35\) and \({\text{34}}\,{\text{800}}\,{\text{000}}\)) A1 N2
[2 marks]
Total [6 marks]
Question
An environmental group records the numbers of coyotes and foxes in a wildlife reserve after \(t\) years, starting on 1 January 1995.
Let \(c\) be the number of coyotes in the reserve after \(t\) years. The following table shows the number of coyotes after \(t\) years.
The relationship between the variables can be modelled by the regression equation \(c = at + b\).
Find the value of \(a\) and of \(b\).
Use the regression equation to estimate the number of coyotes in the reserve when \(t = 7\).
Let \(f\) be the number of foxes in the reserve after \(t\) years. The number of foxes can be modelled by the equation \(f = \frac{{2000}}{{1 + 99{{\text{e}}^{ – kt}}}}\), where \(k\) is a constant.
Find the number of foxes in the reserve on 1 January 1995.
After five years, there were 64 foxes in the reserve. Find \(k\).
During which year were the number of coyotes the same as the number of foxes?
Answer/Explanation
Markscheme
evidence of setup (M1)
eg\(\;\;\;\)correct value for \(a\) or \(b\)
\(13.3823\), \(137.482\)
\(a{\rm{ }} = {\rm{ }}13.4\), \(b{\rm{ }} = {\rm{ }}137\) A1A1 N3
[3 marks]
correct substitution into their regression equation
eg\(\;\;\;13.3823 \times 7 + 137.482\) (A1)
correct calculation
\(231.158\) (A1)
\(231\) (coyotes) (must be an integer) A1 N2
[3 marks]
recognizing \(t = 0\) (M1)
eg\(\;\;\;f(0)\)
correct substitution into the model
eg\(\;\;\;\frac{{2000}}{{1 + 99{{\text{e}}^{ – k(0)}}}},{\text{ }}\frac{{2000}}{{100}}\) (A1)
\(20\) (foxes) A1 N2
[3 marks]
recognizing \((5,{\text{ }}64)\) satisfies the equation (M1)
eg\(\;\;\;f(5) = 64\)
correct substitution into the model
eg\(\;\;\;64 = \frac{{2000}}{{1 + 99{{\text{e}}^{ – k(5)}}}},{\text{ }}64(1 + 99\(e\)^{ – 5k}}) = 2000\) (A1)
\(0.237124\)
\(k = – \frac{1}{5}\ln \left( {\frac{{11}}{{36}}} \right){\text{ (exact), }}0.237{\text{ }}[0.237,{\text{ }}0.238]\) A1 N2
[3 marks]
valid approach (M1)
eg\(\;\;\;c = f\), sketch of graphs
correct working (A1)
eg\(\;\;\;\frac{{2000}}{{1 + 99{{\text{e}}^{ – 0.237124t}}}} = 13.382t + 137.482\), sketch of graphs, table of values
\(t = 12.0403\) (A1)
\(2007\) A1 N2
Note: Exception to the FT rule. Award A1FT on their value of \(t\).
[4 marks]
Total [16 marks]
Question
The price of a used car depends partly on the distance it has travelled. The following table shows the distance and the price for seven cars on 1 January 2010.
The relationship between \(x\) and \(y\) can be modelled by the regression equation \(y = ax + b\).
On 1 January 2010, Lina buys a car which has travelled \(11\,000{\text{ km}}\).
The price of a car decreases by 5% each year.
Lina will sell her car when its price reaches \(10\,000\) dollars.
(i) Find the correlation coefficient.
(ii) Write down the value of \(a\) and of \(b\).
Use the regression equation to estimate the price of Lina’s car, giving your answer to the nearest 100 dollars.
Calculate the price of Lina’s car after 6 years.
Find the year when Lina sells her car.
Answer/Explanation
Markscheme
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
(i) valid approach (M1)
eg\(\,\,\,\,\,\)correct value for \(r\) (or for \(a\) or \(b\) seen in (ii))
\( – 0.994347\)
\(r = – 0.994\) A1 N2
(ii) \( – 1.58095,{\text{ }}33480.3\)
\(a = – 1.58,{\text{ }}b = 33500\) A1A1 N2
[4 marks]
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
correct substitution into their regression equation
eg\(\,\,\,\,\,\)\( – 1.58095(11000){\text{ }} + 33480.3\) (A1)
\(16\,089.85{\text{ }}(16\,120{\text{ from 3sf}})\) (A1)
\({\text{price}} = 16\,100{\text{ }}({\text{dollars}})\) (must be rounded to the nearest 100 dollars) A1 N3
[3 marks]
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
METHOD 1
valid approach (M1)
eg\(\,\,\,\,\,\)\(P \times {({\text{rate}})^t}\)
\({\text{rate}} = 0.95\) (may be seen in their expression) (A1)
correct expression (A1)
eg\(\,\,\,\,\,\)\(16100 \times {0.95^6}\)
\(11\,834.97\)
\(11\,800{\text{ }}({\text{dollars}})\) A1 N2
METHOD 2
attempt to find all six terms (M1)
eg\(\,\,\,\,\,\)\(\left( {\left( {(16\,100 \times 0.95) \times 0.95} \right) \ldots } \right) \times 0.95\), table of values
5 correct values (accept values that round correctly to the nearest dollar)
\(15\,295,{\text{ }}14\,530,{\text{ }}13\,804,{\text{ }}13\,114,{\text{ }}12\,458\) A2
\(11\,835\)
\(11\,800{\text{ }}({\text{dollars}})\) A1 N2
[4 marks]
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
METHOD 1
correct equation (A1)
eg\(\,\,\,\,\,\)\(16\,100 \times {0.95^x}{\text{ = }}10\,000\)
valid attempt to solve (M1)
eg\(\,\,\,\,\,\)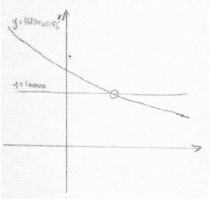
, using logs
9.28453 (A1)
year 2019 A1 N2
METHOD 2
valid approach using table of values (M1)
both crossover values (accept values that round correctly to the nearest dollar) A2
eg\(\,\,\,\,\,\)\({\text{P}} = 10\,147{\text{ }}({\text{1 Jan 2019}}),{\text{ P}} = 9\,639.7{\text{ }}({\text{1 Jan 2020}})\)
year 2019 A1 N2
[4 marks]
Question
Adam is a beekeeper who collected data about monthly honey production in his bee hives. The data for six of his hives is shown in the following table.
The relationship between the variables is modelled by the regression line with equation \(P = aN + b\).
Adam has 200 hives in total. He collects data on the monthly honey production of all the hives. This data is shown in the following cumulative frequency graph.
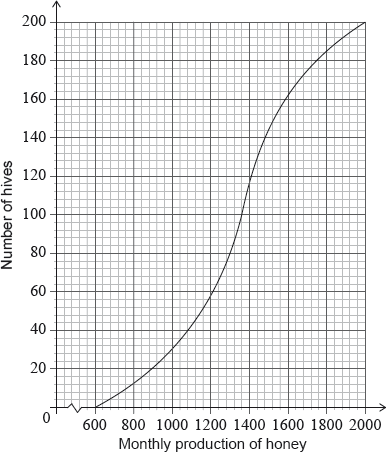
Adam’s hives are labelled as low, regular or high production, as defined in the following table.
Adam knows that 128 of his hives have a regular production.
Write down the value of \(a\) and of \(b\).
Use this regression line to estimate the monthly honey production from a hive that has 270 bees.
Write down the number of low production hives.
Find the value of \(k\);
Find the number of hives that have a high production.
Adam decides to increase the number of bees in each low production hive. Research suggests that there is a probability of 0.75 that a low production hive becomes a regular production hive. Calculate the probability that 30 low production hives become regular production hives.
Answer/Explanation
Markscheme
evidence of setup (M1)
eg\(\,\,\,\,\,\)correct value for \(a\) or \(b\)
\(a = 6.96103,{\text{ }}b = – 454.805\)
\(a = 6.96,{\text{ }}b = – 455{\text{ (accept }}6.96x – 455)\) A1A1 N3
[3 marks]
substituting \(N = 270\) into their equation (M1)
eg\(\,\,\,\,\,\)\(6.96(270) – 455\)
1424.67
\(P = 1420{\text{ (g)}}\) A1 N2
[2 marks]
40 (hives) A1 N1
[1 mark]
valid approach (M1)
eg\(\,\,\,\,\,\)\(128 + 40\)
168 hives have a production less than \(k\) (A1)
\(k = 1640\) A1 N3
[3 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(200 – 168\)
32 (hives) A1 N2
[2 marks]
recognize binomial distribution (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(X \sim {\text{B}}(n,{\text{ }}p),{\text{ }}\left( {\begin{array}{*{20}{c}} n \\ r \end{array}} \right){p^r}{(1 – p)^{n – r}}\)
correct values (A1)
eg\(\,\,\,\,\,\)\(n = 40\) (check FT) and \(p = 0.75\) and \(r = 30,{\text{ }}\left( {\begin{array}{*{20}{c}} {40} \\ {30} \end{array}} \right){0.75^{30}}{(1 – 0.75)^{10}}\)
0.144364
0.144 A1 N2
[3 marks]
Question
The following table shows values of ln x and ln y.
The relationship between ln x and ln y can be modelled by the regression equation ln y = a ln x + b.
Find the value of a and of b.
Use the regression equation to estimate the value of y when x = 3.57.
The relationship between x and y can be modelled using the formula y = kxn, where k ≠ 0 , n ≠ 0 , n ≠ 1.
By expressing ln y in terms of ln x, find the value of n and of k.
Answer/Explanation
Markscheme
valid approach (M1)
eg one correct value
−0.453620, 6.14210
a = −0.454, b = 6.14 A1A1 N3
[3 marks]
correct substitution (A1)
eg −0.454 ln 3.57 + 6.14
correct working (A1)
eg ln y = 5.56484
261.083 (260.409 from 3 sf)
y = 261, (y = 260 from 3sf) A1 N3
Note: If no working shown, award N1 for 5.56484.
If no working shown, award N2 for ln y = 5.56484.
[3 marks]
METHOD 1
valid approach for expressing ln y in terms of ln x (M1)
eg \({\text{ln}}\,y = {\text{ln}}\,\left( {k{x^n}} \right),\,\,{\text{ln}}\,\left( {k{x^n}} \right) = a\,{\text{ln}}\,x + b\)
correct application of addition rule for logs (A1)
eg \({\text{ln}}\,k + {\text{ln}}\,\left( {{x^n}} \right)\)
correct application of exponent rule for logs A1
eg \({\text{ln}}\,k + n\,{\text{ln}}\,x\)
comparing one term with regression equation (check FT) (M1)
eg \(n = a,\,\,b = {\text{ln}}\,k\)
correct working for k (A1)
eg \({\text{ln}}\,k = 6.14210,\,\,\,k = {e^{6.14210}}\)
465.030
\(n = – 0.454,\,\,k = 465\) (464 from 3sf) A1A1 N2N2
METHOD 2
valid approach (M1)
eg \({e^{{\text{ln}}\,y}} = {e^{a\,{\text{ln}}\,x + b}}\)
correct use of exponent laws for \({e^{a\,{\text{ln}}\,x + b}}\) (A1)
eg \({e^{a\,{\text{ln}}\,x}} \times {e^b}\)
correct application of exponent rule for \(a\,{\text{ln}}\,x\) (A1)
eg \({\text{ln}}\,{x^a}\)
correct equation in y A1
eg \(y = {x^a} \times {e^b}\)
comparing one term with equation of model (check FT) (M1)
eg \(k = {e^b},\,\,n = a\)
465.030
\(n = – 0.454,\,\,k = 465\) (464 from 3sf) A1A1 N2N2
METHOD 3
valid approach for expressing ln y in terms of ln x (seen anywhere) (M1)
eg \({\text{ln}}\,y = {\text{ln}}\,\left( {k{x^n}} \right),\,\,{\text{ln}}\,\left( {k{x^n}} \right) = a\,{\text{ln}}\,x + b\)
correct application of exponent rule for logs (seen anywhere) (A1)
eg \({\text{ln}}\,\left( {{x^a}} \right) + b\)
correct working for b (seen anywhere) (A1)
eg \(b = {\text{ln}}\,\left( {{e^b}} \right)\)
correct application of addition rule for logs A1
eg \({\text{ln}}\,\left( {{e^b}{x^a}} \right)\)
comparing one term with equation of model (check FT) (M1)
eg \(k = {e^b},\,\,n = a\)
465.030
\(n = – 0.454,\,\,k = 465\) (464 from 3sf) A1A1 N2N2
[7 marks]
Question
The following table shows the mean weight, y kg , of children who are x years old.
The relationship between the variables is modelled by the regression line with equation \(y = ax + b\).
Find the value of a and of b.
Write down the correlation coefficient.
Use your equation to estimate the mean weight of a child that is 1.95 years old.
Answer/Explanation
Markscheme
valid approach (M1)
eg correct value for a or b (or for r seen in (ii))
a = 1.91966 b = 7.97717
a = 1.92, b = 7.98 A1A1 N3
[3 marks]
0.984674
r = 0.985 A1 N1
[1 mark]
correct substitution into their equation (A1)
eg 1.92 × 1.95 + 7.98
11.7205
11.7 (kg) A1 N2
[2 marks]