Question
Consider the events A and B, where \({\rm{P}}(A) = 0.5\) , \({\rm{P}}(B) = 0.7\) and \({\rm{P}}(A \cap B) = 0.3\) .
The Venn diagram below shows the events A and B, and the probabilities p, q and r.
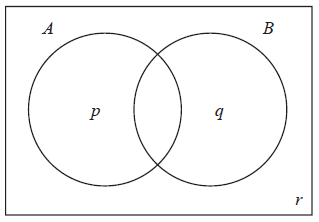
Write down the value of
(i) p ;
(ii) q ;
(iii) r.
Find the value of \({\rm{P}}(A|B’)\) .
Hence, or otherwise, show that the events A and B are not independent.
Answer/Explanation
Markscheme
(i) \(p = 0.2\) A1 N1
(ii) \(q = 0.4\) A1 N1
(iii) \(r = 0.1\) A1 N1
[3 marks]
\({\rm{P}}(A|B’) = \frac{2}{3}\) A2 N2
Note: Award A1 for an unfinished answer such as \(\frac{{0.2}}{{0.3}}\) .
[2 marks]
valid reason R1
e.g. \(\frac{2}{3} \ne 0.5\) , \(0.35 \ne 0.3\)
thus, A and B are not independent AG N0
[1 mark]
Question
The diagram below shows the probabilities for events A and B , with \({\rm{P}}(A’) = p\) .
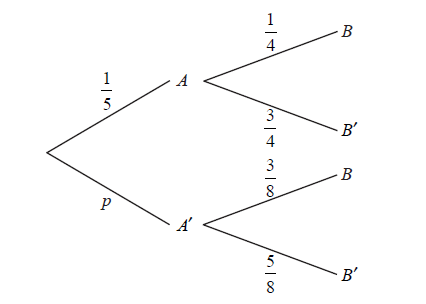
Write down the value of p .
Find \({\rm{P}}(B)\) .
Find \({\rm{P}}(A’|B)\) .
Answer/Explanation
Markscheme
\(p = \frac{4}{5}\) A1 N1
[1 mark]
multiplying along the branches (M1)
e.g. \(\frac{1}{5} \times \frac{1}{4}\) , \(\frac{{12}}{{40}}\)
adding products of probabilities of two mutually exclusive paths (M1)
e.g. \(\frac{1}{5} \times \frac{1}{4} + \frac{4}{5} \times \frac{3}{8}\) , \(\frac{1}{{20}} + \frac{{12}}{{40}}\)
\({\rm{P}}(B) = \frac{{14}}{{40}}\) \(\left( { = \frac{7}{{20}}} \right)\) A1 N2
[3 marks]
appropriate approach which must include \({A’}\) (may be seen on diagram) (M1)
e.g. \(\frac{{{\rm{P}}(A’ \cap B)}}{{{\rm{P}}(B)}}\) (do not accept \(\frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}}\) )
\({\rm{P}}(A’|B) = \frac{{\frac{4}{5} \times \frac{3}{8}}}{{\frac{7}{{20}}}}\) (A1)
\({\rm{P}}(A’|B) = \frac{{12}}{{14}}\) \(\left( { = \frac{6}{7}} \right)\) A1 N2
[3 marks]
Question
The Venn diagram below shows events A and B where \({\rm{P}}(A) = 0.3\) , \({\rm{P}}(A \cup B) = 0.6\) and \({\rm{P}}(A \cap B) = 0.1\) . The values m , n , p and q are probabilities.
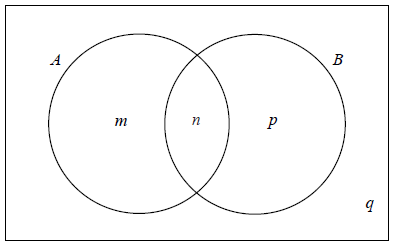
(i) Write down the value of n .
(ii) Find the value of m , of p , and of q .
Find \({\rm{P}}(B’)\) .
Answer/Explanation
Markscheme
(i) \(n = 0.1\) A1 N1
(ii) \(m = 0.2\) , \(p = 0.3\) , \(q = 0.4\) A1A1A1 N3
[4 marks]
appropriate approach
e.g. \({\rm{P}}(B’) = 1 – P(B)\) , \(m + q\) , \(1 – (n + p)\) (M1)
\({\rm{P}}(B’) = 0.6\) A1 N2
[2 marks]
Question
Events A and B are such that \({\rm{P}}(A) = 0.3\) , \({\rm{P}}(B) = 0.6\) and \({\rm{P}}(A \cup B) = 0.7\) .
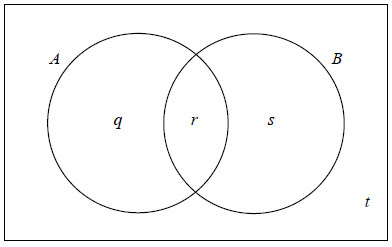
The values q , r , s and t represent probabilities.
Write down the value of t .
(i) Show that \(r = 0.2\) .
(ii) Write down the value of q and of s .
(i) Write down \({\rm{P}}(B’)\) .
(ii) Find \({\rm{P}}(A|B’)\) .
Answer/Explanation
Markscheme
\(t = 0.3\) A1 N1
[1 mark]
(i) correct values A1
e.g. \(0.3 + 0.6 – 0.7\) , \(0.9 – 0.7\)
\(r = 0.2\) AG N0
(ii) \(q = 0.1\) , \(s = 0.4\) A1A1 N2
[3 marks]
(i) \(0.4\) A1 N1
(ii) \({\rm{P}}(A|B’) = \frac{1}{4}\) A2 N2
[3 marks]
Question
Celeste wishes to hire a taxicab from a company which has a large number of taxicabs.
The taxicabs are randomly assigned by the company.
The probability that a taxicab is yellow is 0.4.
The probability that a taxicab is a Fiat is 0.3.
The probability that a taxicab is yellow or a Fiat is 0.6.
Find the probability that the taxicab hired by Celeste is not a yellow Fiat.
Answer/Explanation
Markscheme
recognize need for intersection of Y and F (R1)
eg \({\text{P}}(Y \cap F){\text{, }}0.3 \times 0.4\)
valid approach to find \({\text{P}}(Y \cap F)\) (M1)
eg \({\text{P}}(Y) + {\text{P}}(F) – {\text{P}}(Y \cup F)\), Venn diagram
correct working (may be seen in Venn diagram) (A1)
eg \(0.4 + 0.3 – 0.6\)
\({\text{P}}(Y \cap F) = 0.1\) A1
recognize need for complement of \(Y \cap F\) (M1)
eg \(1 – {\text{P}}(Y \cap F){\text{, }}1 – 0.1\)
\({\text{P}}\left( {(Y \cap F)’} \right) = 0.9\) A1 N3
[6 marks]
Question
Bill and Andrea play two games of tennis. The probability that Bill wins the first game is \(\frac{4}{5}\).
If Bill wins the first game, the probability that he wins the second game is \(\frac{5}{6}\).
If Bill loses the first game, the probability that he wins the second game is \(\frac{2}{3}\).
Copy and complete the following tree diagram. (Do not write on this page.)
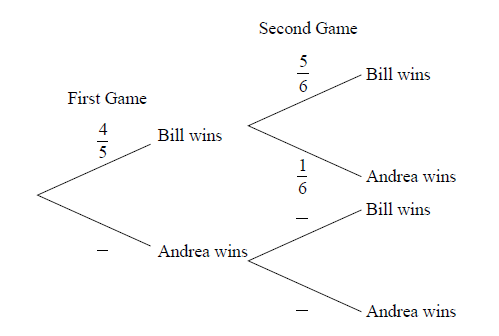
Find the probability that Bill wins the first game and Andrea wins the second game.
Find the probability that Bill wins at least one game.
Given that Bill wins at least one game, find the probability that he wins both games.
Answer/Explanation
Markscheme
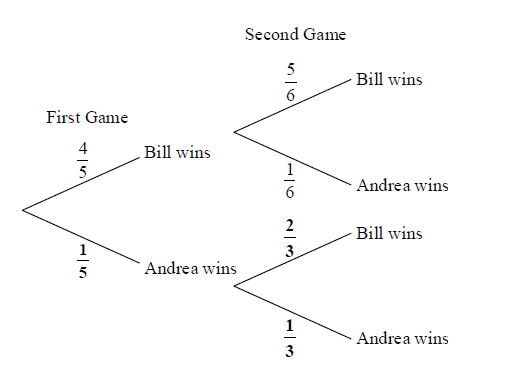A1A1A1 N3
Note: Award A1 for each correct bold probability.
[3 marks]
multiplying along the branches (may be seen on diagram) (M1)
eg \(\frac{4}{5} \times \frac{1}{6}\)
\(\frac{4}{{30}}\left( {\frac{2}{{15}}} \right)\) A1 N2
[2 marks]
METHOD 1
multiplying along the branches (may be seen on diagram) (M1)
eg \(\frac{4}{5} \times \frac{5}{6},{\text{ }}\frac{4}{5} \times \frac{1}{6},{\text{ }}\frac{1}{5} \times \frac{2}{3}\)
adding their probabilities of three mutually exclusive paths (M1)
eg \(\frac{4}{5} \times \frac{5}{6} + \frac{4}{5} \times \frac{1}{6} + \frac{1}{5} \times \frac{2}{3},{\text{ }}\frac{4}{5} + \frac{1}{5} \times \frac{2}{3}\)
correct simplification (A1)
eg \(\frac{{20}}{{30}} + \frac{4}{{30}} + \frac{2}{{15}},{\text{ }}\frac{2}{3} + \frac{2}{{15}} + \frac{2}{{15}}\)
\(\frac{{28}}{{30}}{\text{ }}\left( { = \frac{{14}}{{15}}} \right)\) A1 N3
METHOD 2
recognizing “Bill wins at least one” is complement of “Andrea wins 2” (R1)
eg finding P (Andrea wins 2)
P (Andrea wins both) \( = \frac{1}{5} \times \frac{1}{3}\) (A1)
evidence of complement (M1)
eg \(1 – p,{\text{ }}1 – \frac{1}{{15}}\)
\(\frac{{14}}{{15}}\) A1 N3
[4 marks]
P (B wins both) \(\frac{4}{5} \times \frac{5}{6}{\text{ }}\left( { = \frac{2}{3}} \right)\) A1
evidence of recognizing conditional probability (R1)
eg \({\text{P}}(A\left| B \right.),{\text{ P (Bill wins both}}\left| {{\text{Bill wins at least one), tree diagram}}} \right.\)
correct substitution (A2)
eg \(\frac{{\frac{4}{5} \times \frac{5}{6}}}{{\frac{{14}}{{15}}}}\)
\(\frac{{20}}{{28}}{\text{ }}\left( { = \frac{5}{7}} \right)\) A1 N3
[5 marks]
Question
Adam travels to school by car (\(C\)) or by bicycle (\(B\)). On any particular day he is equally likely to travel by car or by bicycle.
The probability of being late (\(L\)) for school is \(\frac{1}{6}\) if he travels by car.
The probability of being late for school is \(\frac{1}{3}\) if he travels by bicycle.
This information is represented by the following tree diagram.
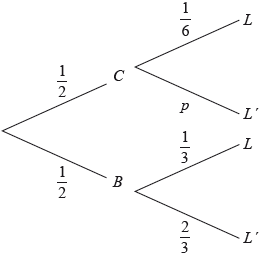
Find the value of \(p\).
Find the probability that Adam will travel by car and be late for school.
Find the probability that Adam will be late for school.
Given that Adam is late for school, find the probability that he travelled by car.
Adam will go to school three times next week.
Find the probability that Adam will be late exactly once.
Answer/Explanation
Markscheme
correct working (A1)
eg\(\;\;\;1 – \frac{1}{6}\)
\(p = \frac{5}{6}\) A1 N2
[2 marks]
multiplying along correct branches (A1)
eg\(\;\;\;\frac{1}{2} \times \frac{1}{6}\)
\({\text{P}}(C \cap L) = \frac{1}{{12}}\) A1 N2
[2 marks]
multiplying along the other branch (M1)
eg\(\;\;\;\frac{1}{2} \times \frac{1}{3}\)
adding probabilities of their \(2\) mutually exclusive paths (M1)
eg\(\;\;\;\frac{1}{2} \times \frac{1}{6} + \frac{1}{2} \times \frac{1}{3}\)
correct working (A1)
eg\(\;\;\;\frac{1}{{12}} + \frac{1}{6}\)
\({\text{P}}(L) = \frac{3}{{12}}\;\;\;\left( { = \frac{1}{4}} \right)\) A1 N3
[4 marks]
recognizing conditional probability (seen anywhere) (M1)
eg\(\;\;\;{\text{P}}(C|L)\)
correct substitution of their values into formula (A1)
eg\(\frac{{\frac{1}{{12}}}}{{\frac{3}{{12}}}}\)
\({\text{P}}(C|L) = \frac{1}{3}\) A1 N2
[3 marks]
valid approach (M1)
eg \(X \sim B\) \(\left({3,{\text{ }}\frac{1}{4}} \right),{\text{ }}\left({\frac{1}{4}} \right){\left({\frac{3}{4}} \right)^2},{\text{ }}\left( {\begin{array}{*{20}{c}}3 \\1\end{array}} \right)\), three ways it could happen
correct substitution (A1)
eg \(\;\;\;\left({\begin{array}{*{20}{c}}3\\1\end{array}}\right){\left({\frac{1}{4}}\right)^1}{\left({\frac{3}{4}} \right)^2},{\text{ }}\frac{1}{4}\times\frac{3}{4}\times\frac{3}{4} + \frac{3}{4} \times\frac{1}{4}\times\frac{3}{4} + \frac{3}{4}\times\frac{3}{4}\times\frac{1}{4}\)
correct working (A1)
eg\(\;\;\;3\left( {\frac{1}{4}} \right)\left( {\frac{9}{{16}}} \right),{\text{ }}\frac{9}{{64}} + \frac{9}{{64}} + \frac{9}{{64}}\)
\(\frac{{27}}{{64}}\) A1 N2
[4 marks]
Total [15 marks]
Question
In a class of 21 students, 12 own a laptop, 10 own a tablet, and 3 own neither.
The following Venn diagram shows the events “own a laptop” and “own a tablet”.
The values \(p\), \(q\), \(r\) and \(s\) represent numbers of students.
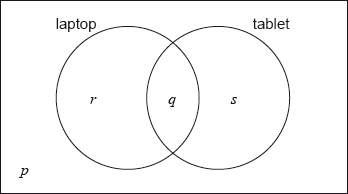
A student is selected at random from the class.
Two students are randomly selected from the class. Let \(L\) be the event a “student owns a laptop”.
(i) Write down the value of \(p\).
(ii) Find the value of \(q\).
(iii) Write down the value of \(r\) and of \(s\).
(i) Write down the probability that this student owns a laptop.
(ii) Find the probability that this student owns a laptop or a tablet but not both.
(i) Copy and complete the following tree diagram. (Do not write on this page.)
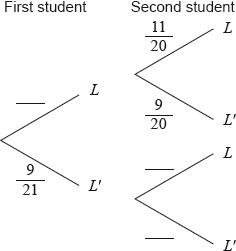
(ii) Write down the probability that the second student owns a laptop given that the first owns a laptop.
Answer/Explanation
Markscheme
(i) \(p = 3\) A1 N1
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)\((12 + 10 + 3) – 21,{\text{ }}22 – 18\)
\(q = 4\) A1 N2
(iii) \(r = 8,{\text{ }}s = 6\) A1A1 N2
(i) \(\frac{{12}}{{21}}{\text{ }}\left( { = \frac{4}{7}} \right)\) A2 N2
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)\(8 + 6,{\text{ }}r + s\)
\(\frac{{14}}{{21}}{\text{ }}\left( { = \frac{2}{3}} \right)\) A1 N2
(i)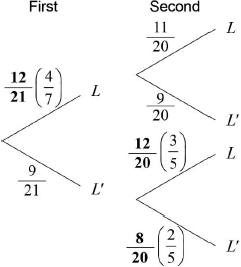 
A1A1A1 N3
(ii) \(\frac{{11}}{{20}}\) A1 N1
[4 marks]
Question
A bag contains 5 green balls and 3 white balls. Two balls are selected at random without replacement.
Complete the following tree diagram.
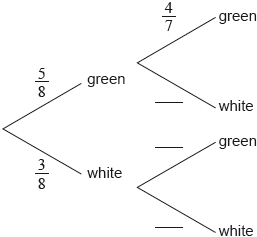
Find the probability that exactly one of the selected balls is green.
Answer/Explanation
Markscheme
correct probabilities
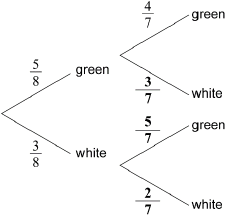A1A1A1 N3
Note: Award A1 for each correct bold answer.
[3 marks]
multiplying along branches (M1)
eg\(\,\,\,\,\,\)\(\frac{5}{8} \times \frac{3}{7},{\text{ }}\frac{3}{8} \times \frac{5}{7},{\text{ }}\frac{{15}}{{56}}\)
adding probabilities of correct mutually exclusive paths (A1)
eg\(\,\,\,\,\,\)\(\frac{5}{8} \times \frac{3}{7} + \frac{3}{8} \times \frac{5}{7},{\text{ }}\frac{{15}}{{56}} + \frac{{15}}{{56}}\)
\(\frac{{30}}{{56}}{\text{ }}\left( { = \frac{{15}}{{28}}} \right)\) A1 N2
[3 marks]
Question
Pablo drives to work. The probability that he leaves home before 07:00 is \(\frac{3}{4}\).
If he leaves home before 07:00 the probability he will be late for work is \(\frac{1}{8}\).
If he leaves home at 07:00 or later the probability he will be late for work is \(\frac{5}{8}\).
Copy and complete the following tree diagram.
Find the probability that Pablo leaves home before 07:00 and is late for work.
Find the probability that Pablo is late for work.
Given that Pablo is late for work, find the probability that he left home before 07:00.
Two days next week Pablo will drive to work. Find the probability that he will be late at least once.
Answer/Explanation
Markscheme
A1A1A1 N3
Note: Award A1 for each bold fraction.
[3 marks]
multiplying along correct branches (A1)
eg \(\frac{3}{4} \times \frac{1}{8}\)
P(leaves before 07:00 ∩ late) = \(\frac{3}{32}\) A1 N2
[2 marks]
multiplying along other “late” branch (M1)
eg \(\frac{1}{4} \times \frac{5}{8}\)
adding probabilities of two mutually exclusive late paths (A1)
eg \(\left( {\frac{3}{4} \times \frac{1}{8}} \right) + \left( {\frac{1}{4} \times \frac{5}{8}} \right),\,\,\frac{3}{{32}} + \frac{5}{{32}}\)
\({\text{P}}\left( L \right) = \frac{8}{{32}}\,\,\left( { = \frac{1}{4}} \right)\) A1 N2
[3 marks]
recognizing conditional probability (seen anywhere) (M1)
eg \({\text{P}}\left( {A|B} \right),\,\,{\text{P}}\left( {{\text{before 7}}|{\text{late}}} \right)\)
correct substitution of their values into formula (A1)
eg \(\frac{{\frac{3}{{32}}}}{{\frac{1}{4}}}\)
\({\text{P}}\left( {{\text{left before 07:00}}|{\text{late}}} \right) = \frac{3}{8}\) A1 N2
[3 marks]
valid approach (M1)
eg 1 − P(not late twice), P(late once) + P(late twice)
correct working (A1)
eg \(1 – \left( {\frac{3}{4} \times \frac{3}{4}} \right),\,\,2 \times \frac{1}{4} \times \frac{3}{4} + \frac{1}{4} \times \frac{1}{4}\)
\(\frac{7}{{16}}\) A1 N2
[3 marks]