Question
A fisherman catches 200 fish to sell. He measures the lengths, l cm of these fish, and the results are shown in the frequency table below.
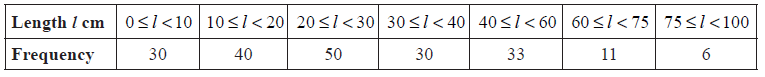
Calculate an estimate for the standard deviation of the lengths of the fish.
A cumulative frequency diagram is given below for the lengths of the fish.
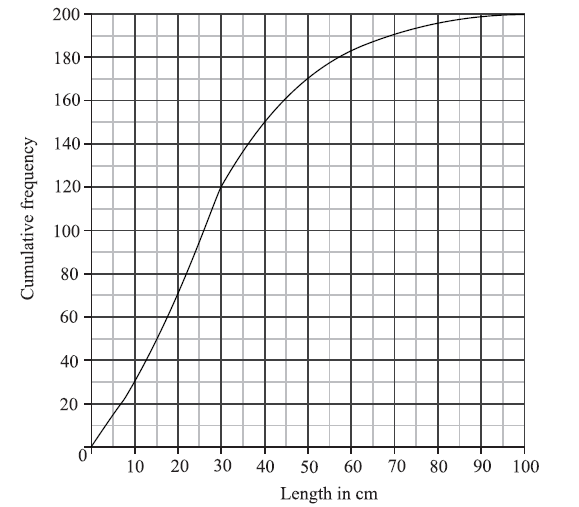
Use the graph to answer the following.
(i) Estimate the interquartile range.
(ii) Given that \(40\% \) of the fish have a length more than \(k{\text{ cm}}\), find the value of k.
In order to sell the fish, the fisherman classifies them as small, medium or large.
Small fish have a length less than \(20{\text{ cm}}\).
Medium fish have a length greater than or equal to \(20{\text{ cm}}\) but less than \(60{\text{ cm}}\).
Large fish have a length greater than or equal to \(60{\text{ cm}}\).
Write down the probability that a fish is small.
The cost of a small fish is \(\$ 4\), a medium fish \(\$ 10\), and a large fish \(\$ 12\).
Copy and complete the following table, which gives a probability distribution for the cost \(\$ X\) .
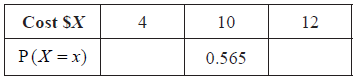
Find \({\text{E}}(X)\) .
Answer/Explanation
Markscheme
evidence of using mid-interval values (5, 15, 25, 35, 50, 67.5, 87.5) (M1)
\(\sigma = 19.8\) (cm) A2 N3
[3 marks]
(i) \({Q_1} = 15\) , \({Q_3} = 40\) (A1)(A1)
\(IQR = 25\) (accept any notation that suggests the interval 15 to 40) A1 N3
(ii) METHOD 1
\(60\% \) have a length less than k (A1)
\(0.6 \times 200 = 120\) (A1)
\(k = 30\) (cm) A1 N2
METHOD 2
\(0.4 \times 200 = 80\) (A1)
\(200 – 80 = 120\) (A1)
\(k = 30\) (cm) A1 N2
[6 marks]
\(l < 20{\text{ cm}} \Rightarrow 70{\text{ fish}}\) (M1)
\({\rm{P(small)}} = \frac{{70}}{{200}}( = 0.35)\) A1 N2
[2 marks]
 A1A1 N2
A1A1 N2
[2 marks]
correct substitution (of their p values) into formula for \({\text{E}}(X)\) (A1)
e.g. \(4 \times 0.35 + 10 \times 0.565 + 12 \times 0.085\)
\({\text{E}}(X) = 8.07\) (accept \(\$ 8.07\)) A1 N2
[2 marks]
Question
A company uses two machines, A and B, to make boxes. Machine A makes \(60\% \) of the boxes.
\(80\% \) of the boxes made by machine A pass inspection.
\(90\% \) of the boxes made by machine B pass inspection.
A box is selected at random.
Find the probability that it passes inspection.
The company would like the probability that a box passes inspection to be 0.87.
Find the percentage of boxes that should be made by machine B to achieve this.
Answer/Explanation
Markscheme
evidence of valid approach involving A and B (M1)
e.g. \({\rm{P}}(A \cap {\rm{pass}}) + {\rm{P}}(B \cap {\rm{pass}})\) , tree diagram
correct expression (A1)
e.g. \({\rm{P}}({\rm{pass}}) = 0.6 \times 0.8 + 0.4 \times 0.9\)
\({\rm{P}}({\rm{pass}}) = 0.84\) A1 N2
[3 marks]
evidence of recognizing complement (seen anywhere) (M1)
e.g. \({\rm{P}}(B) = x\) , \({\rm{P}}(A) = 1 – x\) , \(1 – {\rm{P}}(B)\) , \(100 – x\) , \(x + y = 1\)
evidence of valid approach (M1)
e.g. \(0.8(1 – x) + 0.9x\) , \(0.8x + 0.9y\)
correct expression A1
e.g. \(0.87 = 0.8(1 – x) + 0.9x\) , \(0.8 \times 0.3 + 0.9 \times 0.7 = 0.87\) , \(0.8x + 0.9y = 0.87\)
\(70\% \) from B A1 N2
[4 marks]
Question
Samantha goes to school five days a week. When it rains, the probability that she goes to school by bus is 0.5. When it does not rain, the probability that she goes to school by bus is 0.3. The probability that it rains on any given day is 0.2.
On a randomly selected school day, find the probability that Samantha goes to school by bus.
Given that Samantha went to school by bus on Monday, find the probability that it was raining.
In a randomly chosen school week, find the probability that Samantha goes to school by bus on exactly three days.
After \(n\) school days, the probability that Samantha goes to school by bus at least once is greater than \(0.95\). Find the smallest value of \(n\).
Answer/Explanation
Markscheme
appropriate approach (M1)
eg \({\text{P}}(R \cap B) + {\text{P}}(R’ \cap B)\), tree diagram,
one correct multiplication (A1)
eg \(0.2 \times 0.5,{\text{ }}0.24\)
correct working (A1)
eg \(0.2 \times 0.5 + 0.8 \times 0.3,{\text{ }}0.1 + 0.24\)
\({\text{P(bus)}} = 0.34 {\text{(exact)}}\) A1 N3
[4 marks]
recognizing conditional probability (R1)
eg \({\text{P}}(A|B) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\)
correct working A1
eg \(\frac{{0.2 \times 0.5}}{{0.34}}\)
\({\text{P}}(R|B) = \frac{5}{{17}},{\text{ }}0.294\) A1 N2
[3 marks]
recognizing binomial probability (R1)
eg \(X \sim {\text{B}}(n,{\text{ }}p)\), \(\left( \begin{array}{c}5\\3\end{array} \right)\) \({(0.34)^3},{\text{ }}{(0.34)^3}{(1 – 0.34)^2}\)
\({\text{P}}(X = 3) = 0.171\) A1 N2
[2 marks]
METHOD 1
evidence of using complement (seen anywhere) (M1)
eg \(1 – {\text{P (none), }}1 – 0.95\)
valid approach (M1)
eg \(1 – {\text{P (none)}} > 0.95,{\text{ P (none)}} < 0.05,{\text{ }}1 – {\text{P (none)}} = 0.95\)
correct inequality (accept equation) A1
eg \(1 – {(0.66)^n} > 0.95,{\text{ }}{(0.66)^n} = 0.05\)
\(n > 7.209{\text{ (accept }}n = 7.209{\text{)}}\) (A1)
\(n = 8\) A1 N3
METHOD 2
valid approach using guess and check/trial and error (M1)
eg finding \({\text{P}}(X \geqslant 1)\) for various values of n
seeing the “cross over” values for the probabilities A1A1
\(n = 7,{\text{ P}}(X \geqslant 1) = 0.9454,{\text{ }}n = 8,{\text{ P}}(X \geqslant 1) = 0.939\)
recognising \(0.9639 > 0.95\) (R1)
\(n = 8\) A1 N3
[5 marks]
Question
Let \(C\) and \(D\) be independent events, with \({\text{P}}(C) = 2k\) and \({\text{P}}(D) = 3{k^2}\), where \(0 < k < 0.5\).
Write down an expression for \({\text{P}}(C \cap D)\) in terms of \(k\).
Given that \({\text{P}}(C \cap D) = 0.162\) find \(k\).
Find \({\text{P}}(C’|D)\).
Answer/Explanation
Markscheme
\({\text{P}}(C \cap D) = 2k \times 3{k^2}\) (A1)
\({\text{P}}(C \cap D) = 6{k^3}\) A1 N2
[2 marks]
their correct equation (A1)
eg\(\;\;\;2k \times 3{k^2} = 0.162,{\text{ }}6{k^3} = 0.162\)
\(k = 0.3\) A1 N2
METHOD 1
finding their \({\text{P}}(C’ \cap D)\) (seen anywhere) (A1)
eg \(0.4 \times 0.27,0.27 – 0.162,0.108\)
correct substitution into conditional probability formula (A1)
eg\(\;\;\;{\text{P}}(C’|D) = \frac{{{\text{P}}(C’ \cap D)}}{{0.27}},{\text{ }}\frac{{(1 – 2k)(3{k^2})}}{{3{k^2}}}\)
\({\text{P}}(C’|D) = 0.4\) A1 N2
METHOD 2
recognizing \({\text{P}}(C’|D) = {\text{P}}(C’)\) A1
finding their \({\text{P}}(C’) = 1 – {\text{P}}(C)\) (only if first line seen) (A1)
eg\(\;\;\;1 – 2k,{\text{ }}1 – 0.6\)
\({\text{P}}(C’|D) = 0.4\) A1 N2
[3 marks]
Total [7 marks]
Question
Two events A and B are such that P(A) = 0.62 and P\(\left( {A \cap B} \right)\) = 0.18.
Find P(A ∩ B′ ).
Given that P((A ∪ B)′ ) = 0.19, find P(A | B′ ).
Answer/Explanation
Markscheme
valid approach
eg Venn diagram, P(A) − P (A ∩ B), 0.62 − 0.18 (M1)
P(A ∩ B’ ) = 0.44 A1 N2
[2 marks]
valid approach to find either P(B′ ) or P(B) (M1)
eg (seen anywhere), 1 − P(A ∩ B′ ) − P((A ∪ B)′ )
correct calculation for P(B′ ) or P(B) (A1)
eg 0.44 + 0.19, 0.81 − 0.62 + 0.18
correct substitution into \(\frac{{{\text{P}}\left( {A \cap B’} \right)}}{{{\text{P}}\left( {B’} \right)}}\) (A1)
eg \(\frac{{0.44}}{{0.19 + 0.44}},\,\,\frac{{0.44}}{{1 – 0.37}}\)
0.698412
P(A | B′ ) = \(\frac{{44}}{{63}}\) (exact), 0.698 A1 N3
[4 marks]
