Question
A fisherman catches 200 fish to sell. He measures the lengths, l cm of these fish, and the results are shown in the frequency table below.
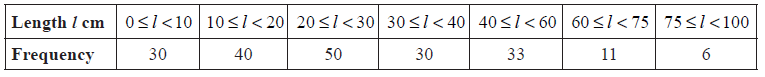
Calculate an estimate for the standard deviation of the lengths of the fish.
A cumulative frequency diagram is given below for the lengths of the fish.
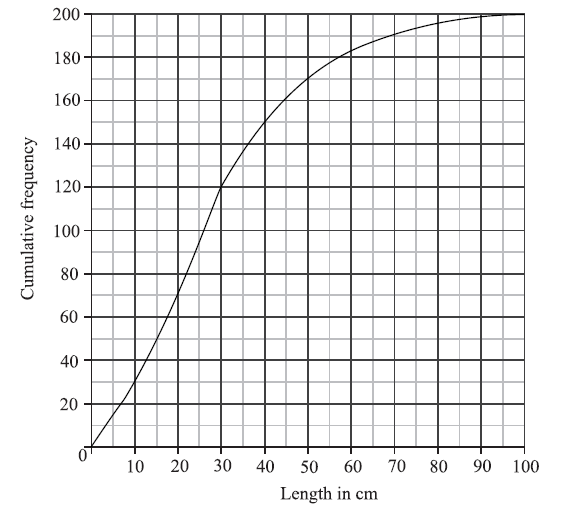
Use the graph to answer the following.
(i) Estimate the interquartile range.
(ii) Given that \(40\% \) of the fish have a length more than \(k{\text{ cm}}\), find the value of k.
In order to sell the fish, the fisherman classifies them as small, medium or large.
Small fish have a length less than \(20{\text{ cm}}\).
Medium fish have a length greater than or equal to \(20{\text{ cm}}\) but less than \(60{\text{ cm}}\).
Large fish have a length greater than or equal to \(60{\text{ cm}}\).
Write down the probability that a fish is small.
The cost of a small fish is \(\$ 4\), a medium fish \(\$ 10\), and a large fish \(\$ 12\).
Copy and complete the following table, which gives a probability distribution for the cost \(\$ X\) .
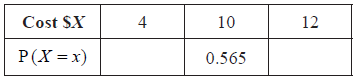
Find \({\text{E}}(X)\) .
Answer/Explanation
Markscheme
evidence of using mid-interval values (5, 15, 25, 35, 50, 67.5, 87.5) (M1)
\(\sigma = 19.8\) (cm) A2 N3
[3 marks]
(i) \({Q_1} = 15\) , \({Q_3} = 40\) (A1)(A1)
\(IQR = 25\) (accept any notation that suggests the interval 15 to 40) A1 N3
(ii) METHOD 1
\(60\% \) have a length less than k (A1)
\(0.6 \times 200 = 120\) (A1)
\(k = 30\) (cm) A1 N2
METHOD 2
\(0.4 \times 200 = 80\) (A1)
\(200 – 80 = 120\) (A1)
\(k = 30\) (cm) A1 N2
[6 marks]
\(l < 20{\text{ cm}} \Rightarrow 70{\text{ fish}}\) (M1)
\({\rm{P(small)}} = \frac{{70}}{{200}}( = 0.35)\) A1 N2
[2 marks]
 A1A1 N2
A1A1 N2
[2 marks]
correct substitution (of their p values) into formula for \({\text{E}}(X)\) (A1)
e.g. \(4 \times 0.35 + 10 \times 0.565 + 12 \times 0.085\)
\({\text{E}}(X) = 8.07\) (accept \(\$ 8.07\)) A1 N2
[2 marks]
Question
The cumulative frequency curve below represents the heights of 200 sixteen-year-old boys.
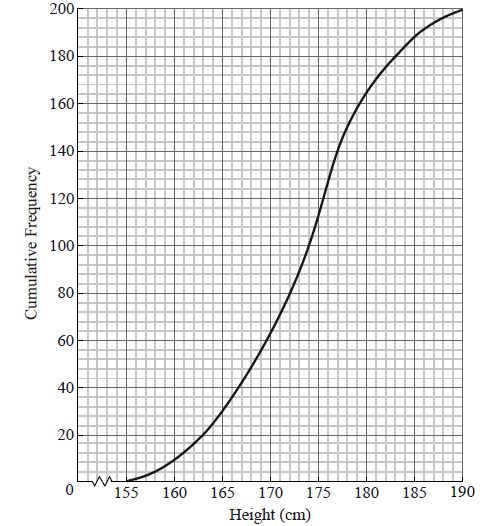
Use the graph to answer the following.
Write down the median value.
A boy is chosen at random. Find the probability that he is shorter than \(161{\text{ cm}}\).
Given that \(82\% \) of the boys are taller than \(h{\text{ cm}}\), find h .
Answer/Explanation
Markscheme
\({\text{median}} = 174 {\text{(cm)}}\) A1 N1
[1 mark]
attempt to find number shorter than 161 (M1)
e.g. line on graph, 12 boys
\(p = \frac{{12}}{{200}}( = 0.06)\) A1 N2
[2 marks]
METHOD 1
\(18\% \) have a height less than h (A1)
\(0.18 \times 200 = 36\) (36 may be seen as a line on the graph) (A1)
\(h = 166\) (cm) A1 N2
METHOD 2
\(0.82 \times 200 = 164\) (164 may be seen as a line on the graph) (A1)
\(200 – 164 = 36\) (A1)
\(h = 166\) (cm) A1 N2
[3 marks]
Question
The histogram below shows the time T seconds taken by 93 children to solve a puzzle.
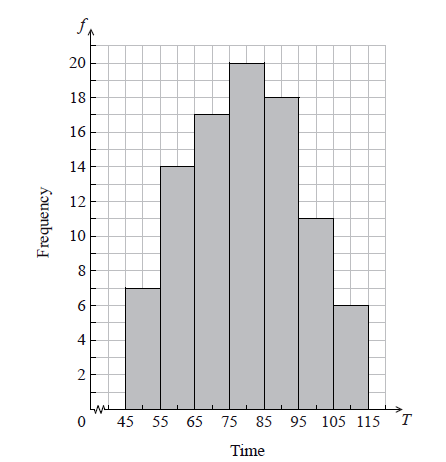
The following is the frequency distribution for T .
(i) Write down the value of p and of q .
(ii) Write down the median class.
A child is selected at random. Find the probability that the child takes less than 95 seconds to solve the puzzle.
Consider the class interval \(45 \le T < 55\) .
(i) Write down the interval width.
(ii) Write down the mid-interval value.
Hence find an estimate for the
(i) mean;
(ii) standard deviation.
John assumes that T is normally distributed and uses this to estimate the probability that a child takes less than 95 seconds to solve the puzzle.
Find John’s estimate.
Answer/Explanation
Answer/Explanation
Markscheme
(i) \(p = 17\) , \(q = 11\) A1A1 N2
(ii) \(75 \le T < 85\) A1 N1
[3 marks]
evidence of valid approach (M1)
e.g. adding frequencies
\(\frac{{76}}{{93}} = 0.8172043 \ldots \)
\({\rm{P}}(T < 95) = \frac{{76}}{{93}} = 0.817\) A1 N2
[2 marks]
(i) 10 A1 N1
(ii) 50 A1 N1
[2 marks]
(i) evidence of approach using mid-interval values (may be seen in part (ii)) (M1)
\(79.1397849\)
\(\overline x = 79.1\) A2 N3
(ii) \(16.4386061\)
\(\sigma = 16.4\) A1 N1
[4 marks]
e.g. standardizing, \(z = 0.9648 \ldots \)
\(0.8326812\)
\({\rm{P}}(T < 95) = 0.833\) A1 N2
[2 marks]
Question
A Ferris wheel with diameter \(122\) metres rotates clockwise at a constant speed. The wheel completes \(2.4\) rotations every hour. The bottom of the wheel is \(13\) metres above the ground.
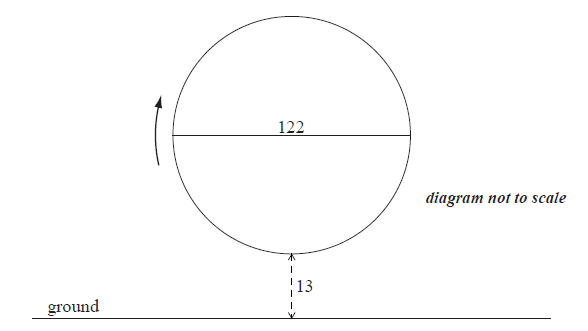

A seat starts at the bottom of the wheel.
After t minutes, the height \(h\) metres above the ground of the seat is given by\[h = 74 + a\cos bt {\rm{ .}}\]
Find the maximum height above the ground of the seat.
(i) Show that the period of \(h\) is \(25\) minutes.
(ii) Write down the exact value of \(b\) .
(b) (i) Show that the period of \(h\) is \(25\) minutes.
(ii) Write down the exact value of \(b\) .
(c) Find the value of \(a\) .
(d) Sketch the graph of \(h\) , for \(0 \le t \le 50\) .
Find the value of \(a\) .
Sketch the graph of \(h\) , for \(0 \le t \le 50\) .
In one rotation of the wheel, find the probability that a randomly selected seat is at least \(105\) metres above the ground.
Answer/Explanation
Markscheme
valid approach (M1)
eg \(13 + {\rm{diameter}}\) , \(13 + 122\)
maximum height \( = 135\) (m) A1 N2
[2 marks]
(i) period \( = \frac{{60}}{{2.4}}\) A1
period \( = 25\) minutes AG N0
(ii) \(b = \frac{{2\pi }}{{25}}\) \(( = 0.08\pi )\) A1 N1
[2 marks]
(a) (i) period \( = \frac{{60}}{{2.4}}\) A1
period \( = 25\) minutes AG N0
(ii) \(b = \frac{{2\pi }}{{25}}\) \(( = 0.08\pi )\) A1 N1
[2 marks]
(b) METHOD 1
valid approach (M1)
eg \({\rm{max}} – 74\) , \(\left| a \right| = \frac{{135 – 13}}{2}\) , \(74 – 13\)
\(\left| a \right| = 61\) (accept \(a = 61\) ) (A1)
\(a = – 61\) A1 N2
METHOD 2
attempt to substitute valid point into equation for h (M1)
eg \(135 = 74 + a\cos \left( {\frac{{2\pi \times 12.5}}{{25}}} \right)\)
correct equation (A1)
eg \(135 = 74 + a\cos (\pi )\) , \(13 = 74 + a\)
\(a = – 61\) A1 N2
[3 marks]
(c)
A1A1A1A1 N4
Note: Award A1 for approximately correct domain, A1 for approximately correct range,
A1 for approximately correct sinusoidal shape with \(2\) cycles.
Only if this last A1 awarded, award A1 for max/min in approximately correct positions.
[4 marks]
Total [9 marks]
METHOD 1
valid approach (M1)
eg \({\rm{max}} – 74\) , \(\left| a \right| = \frac{{135 – 13}}{2}\) , \(74 – 13\)
\(\left| a \right| = 61\) (accept \(a = 61\) ) (A1)
\(a = – 61\) A1 N2
METHOD 2
attempt to substitute valid point into equation for h (M1)
eg \(135 = 74 + a\cos \left( {\frac{{2\pi \times 12.5}}{{25}}} \right)\)
correct equation (A1)
eg \(135 = 74 + a\cos (\pi )\) , \(13 = 74 + a\)
\(a = – 61\) A1 N2
[3 marks]
A1A1A1A1 N4
Note: Award A1 for approximately correct domain, A1 for approximately correct range,
A1 for approximately correct sinusoidal shape with \(2\) cycles.
Only if this last A1 awarded, award A1 for max/min in approximately correct positions.
[4 marks]
setting up inequality (accept equation) (M1)
eg \(h > 105\) , \(105 = 74 + a\cos bt\) , sketch of graph with line \(y = 105\)
any two correct values for t (seen anywhere) A1A1
eg \(t = 8.371 \ldots \) , \(t = 16.628 \ldots \) , \(t = 33.371 \ldots \) , \(t = 41.628 \ldots \)
valid approach M1
eg \(\frac{{16.628 – 8.371}}{{25}}\) , \(\frac{{{t_1} – {t_2}}}{{25}}\) , \(\frac{{2 \times 8.257}}{{50}}\) , \(\frac{{2(12.5 – 8.371)}}{{25}}\)
\(p = 0.330\) A1 N2
[5 marks]
Question
A bag contains four gold balls and six silver balls.
Two balls are drawn at random from the bag, with replacement. Let \(X\) be the number of gold balls drawn from the bag.
Fourteen balls are drawn from the bag, with replacement.
(i) Find \({\rm{P}}(X = 0)\) .
(ii) Find \({\rm{P}}(X = 1)\) .
(iii) Hence, find \({\rm{E}}(X)\) .
Hence, find \({\rm{E}}(X)\) .
Find the probability that exactly five of the balls are gold.
Find the probability that at most five of the balls are gold.
Given that at most five of the balls are gold, find the probability that exactly five of the balls are gold. Give the answer correct to two decimal places.
Answer/Explanation
Markscheme
METHOD 1
(i) appropriate approach (M1)
eg \(\frac{6}{{10}} \times \frac{6}{{10}}\) , \(\frac{6}{{10}} \times \frac{5}{9}\) , \(\frac{6}{{10}} \times \frac{5}{{10}}\)
\({\rm{P}}(X = 0) = \frac{9}{{25}} = 0.36\) A1 N2
(ii) multiplying one pair of gold and silver probabilities (M1)
eg \(\frac{6}{{10}} \times \frac{4}{{10}}\) , \(\frac{6}{{10}} \times \frac{4}{9}\) , 0.24
adding the product of both pairs of gold and silver probabilities (M1)
eg \(\frac{6}{{10}} \times \frac{4}{{10}} \times 2\) , \(\frac{6}{{10}} \times \frac{4}{9} + \frac{4}{{10}} \times \frac{6}{9}\)
\({\rm{P}}(X = 1) = \frac{{12}}{{25}} = 0.48\) A1 N3
(iii)
\({\rm{P}}(X = 2) = 0.16\) (seen anywhere) (A1)
correct substitution into formula for \({\rm{E}}(X)\) (A1)
eg \(0 \times 0.36 + 1 \times 0.48 + 2 \times 0.16\) , \(0.48 + 0.32\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
METHOD 2
(i) evidence of recognizing binomial (may be seen in part (ii)) (M1)
eg \(X \sim {\rm{B}}(2,0.6)\) , \(\left( \begin{array}{l}
2\\
0
\end{array} \right){(0.4)^2}{(0.6)^0}\)
correct probability for use in binomial (A1)
eg \(p = 0.4\) , \(X \sim {\rm{B}}(2,0.4)\) , \(^2{C_0}{(0.4)^0}{(0.6)^2}\)
\({\rm{P}}(X = 0) = \frac{9}{{25}} = 0.36\) A1 N3
(ii) correct set up (A1)
eg \(_2{C_1}{(0.4)^1}{(0.6)^1}\)
\({\rm{P}}(X = 1) = \frac{{12}}{{25}} = 0.48\) A1 N2
(iii)
attempt to substitute into \(np\) (M1)
eg \(2 \times 0.6\)
correct substitution into \(np\) (A1)
eg \(2 \times 0.4\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
[8 marks]
METHOD 1
\({\rm{P}}(X = 2) = 0.16\) (seen anywhere) (A1)
correct substitution into formula for \({\rm{E}}(X)\) (A1)
eg \(0 \times 0.36 + 1 \times 0.48 + 2 \times 0.16\) , \(0.48 + 0.32\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
METHOD 2
attempt to substitute into \(np\) (M1)
eg \(2 \times 0.6\)
correct substitution into \(np\) (A1)
eg \(2 \times 0.4\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
[3 marks]
Let \(Y\) be the number of gold balls drawn from the bag.
evidence of recognizing binomial (seen anywhere) (M1)
eg \(_{14}{C_5}{(0.4)^5}{(0.6)^9}\) , \({\rm{B}}(14,0.4)\)
\({\rm{P}}(Y = 5) = 0.207\) A1 N2
[2 marks]
recognize need to find \({\rm{P}}(Y \le 5)\) (M1)
\({\rm{P}}(Y \le 5) = 0.486\) A1 N2
[2 marks]
Let \(Y\) be the number of gold balls drawn from the bag.
recognizing conditional probability (M1)
eg \({\rm{P}}(A|B)\) , \({\rm{P}}(Y = 5|Y \le 5)\) , \(\frac{{{\rm{P}}(Y = 5)}}{{{\rm{P}}(Y \le 5)}}\) , \(\frac{{0.207}}{{0.486}}\)
\({\rm{P}}(Y = 5|Y \le 5) = 0.42522518\) (A1)
\({\rm{P}}(Y = 5|Y \le 5) = 0.43\) (to \(2\) dp) A1 N2
[3 marks]
Question
The following cumulative frequency graph shows the monthly income, \(I\) dollars, of \(2000\) families.
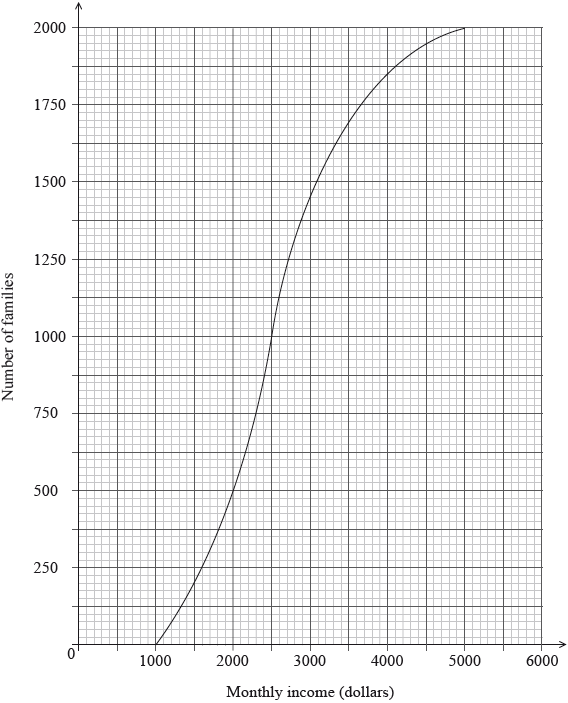
Find the median monthly income.
(i) Write down the number of families who have a monthly income of \(2000\) dollars or less.
(ii) Find the number of families who have a monthly income of more than \(4000\) dollars.
The \(2000\) families live in two different types of housing. The following table gives information about the number of families living in each type of housing and their monthly income \(I\).

Find the value of \(p\).
A family is chosen at random.
(i) Find the probability that this family lives in an apartment.
(ii) Find the probability that this family lives in an apartment, given that its monthly income is greater than \(4000\) dollars.
Estimate the mean monthly income for families living in a villa.
Answer/Explanation
Markscheme
recognizing that the median is at half the total frequency (M1)
eg\(\;\;\;\)\(\frac{{2000}}{2}\)
\(m = 2500{\text{ (dollars)}}\) A1 N2
[2 marks]
(i) \(500\) families have a monthly income less than \(2000\) A1 N1
(ii) correct cumulative frequency, \(1850\) (A1)
subtracting their cumulative frequency from \(2000\) (M1)
eg\(\;\;\;\)\(2000 – 1850\)
\(150\) families have a monthly income of more than \(4000\) dollars A1 N2
Note: If working shown, award M1A1A1 for \(128{\rm{ }} + {\rm{ }}22{\rm{ }} = {\rm{ }}150\), using the table.
[4 marks]
correct calculation (A1)
eg\(\;\;\;\)\(2000 – (436 + 64 + 765 + 28 + 122),{\text{ }}1850 – 500 – 765\) (A1)
\(p = 585\) A1 N2
[2 marks]
(i) correct working (A1)
eg\(\;\;\;\)\(436 + 765 + 28\)
\(0.6145\;\;\;\)(exact) A1 N2
\(\frac{{1229}}{{2000}},{\text{ }}0.615{\text{ }}[0.614,{\text{ }}0.615]\)
(ii) correct working/probability for number of families (A1)
eg\(\;\;\;\)\(122 + 28,{\text{ }}\frac{{150}}{{2000}},{\text{ 0.075}}\)
\(0.186666\)
\(\frac{{28}}{{150}}\;\;\;\left( { = \frac{{14}}{{75}}} \right),{\text{ }}0.187{\text{ }}[0.186,{\text{ }}0.187]\) A1 N2
[4 marks]
evidence of using correct mid-interval values (\(1500,{\rm{ }}3000,{\rm{ }}4500\)) (A1)
attempt to substitute into \(\frac{{\sum {fx} }}{{\sum f }}\) (M1)
eg\(\;\;\;\)\(\frac{{1500 \times 64 + 3000 \times p + 4500 \times 122}}{{64 + 585 + 122}}\)
\(3112.84\)
\(3110{\text{ }}[3110,{\text{ }}3120]{\text{ (dollars)}}\) A1 N2
[3 marks]
Total [15 marks]
Question
Two events A and B are such that P(A) = 0.62 and P\(\left( {A \cap B} \right)\) = 0.18.
Find P(A ∩ B′ ).
Given that P((A ∪ B)′ ) = 0.19, find P(A | B′ ).
Answer/Explanation
Markscheme
valid approach
eg Venn diagram, P(A) − P (A ∩ B), 0.62 − 0.18 (M1)
P(A ∩ B’ ) = 0.44 A1 N2
[2 marks]
valid approach to find either P(B′ ) or P(B) (M1)
eg (seen anywhere), 1 − P(A ∩ B′ ) − P((A ∪ B)′ )
correct calculation for P(B′ ) or P(B) (A1)
eg 0.44 + 0.19, 0.81 − 0.62 + 0.18
correct substitution into \(\frac{{{\text{P}}\left( {A \cap B’} \right)}}{{{\text{P}}\left( {B’} \right)}}\) (A1)
eg \(\frac{{0.44}}{{0.19 + 0.44}},\,\,\frac{{0.44}}{{1 – 0.37}}\)
0.698412
P(A | B′ ) = \(\frac{{44}}{{63}}\) (exact), 0.698 A1 N3
[4 marks]

