Download IITian Academy App for accessing Online Mock Tests and More..
Question
Let \(A\) and \(B\) be independent events, where \({\text{P}}(A) = 0.3\) and \({\text{P}}(B) = 0.6\).
Find \({\text{P}}(A \cap B)\).
Find \({\text{P}}(A \cup B)\).
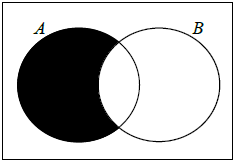
On the following Venn diagram, shade the region that represents \(A \cap B’\).
Find \({\text{P}}(A \cap B’)\).
Answer/Explanation
Markscheme
correct substitution (A1)
eg \(0.3 \times 0.6\)
\({\text{P}}(A \cap B) = 0.18\) A1 N2
[2 marks]
correct substitution (A1)
eg \({\text{P}}(A \cup B) = 0.3 + 0.6 – 0.18\)
\({\text{P}}(A \cup B) = 0.72\) A1 N2
[2 marks]
A1 N1
appropriate approach (M1)
eg \(0.3 – 0.18,{\text{ P}}(A) \times {\text{P}}(B’)\)
\({\text{P}}(A \cap B’) = 0.12\) (may be seen in Venn diagram) A1 N2
[2 marks]
Question
Two events A and B are such that P(A) = 0.62 and P\(\left( {A \cap B} \right)\) = 0.18.
Find P(A ∩ B′ ).
Given that P((A ∪ B)′ ) = 0.19, find P(A | B′ ).
Answer/Explanation
Markscheme
valid approach
eg Venn diagram, P(A) − P (A ∩ B), 0.62 − 0.18 (M1)
P(A ∩ B’ ) = 0.44 A1 N2
[2 marks]
valid approach to find either P(B′ ) or P(B) (M1)
eg 
(seen anywhere), 1 − P(A ∩ B′ ) − P((A ∪ B)′ )
correct calculation for P(B′ ) or P(B) (A1)
eg 0.44 + 0.19, 0.81 − 0.62 + 0.18
correct substitution into \(\frac{{{\text{P}}\left( {A \cap B’} \right)}}{{{\text{P}}\left( {B’} \right)}}\) (A1)
eg \(\frac{{0.44}}{{0.19 + 0.44}},\,\,\frac{{0.44}}{{1 – 0.37}}\)
0.698412
P(A | B′ ) = \(\frac{{44}}{{63}}\) (exact), 0.698 A1 N3
[4 marks]