Question
In any given season, a soccer team plays 65 % of their games at home.
When the team plays at home, they win 83 % of their games.
When they play away from home, they win 26 % of their games.
The team plays one game.
Find the probability that the team wins the game.
If the team does not win the game, find the probability that the game was played at home.
Answer/Explanation
Markscheme
appropriate approach (M1)
e.g. tree diagram or a table
\({\rm{P(win)}} = {\rm{P}}(H \cap W) + {\rm{P}}(A \cap W)\) (M1)
\( = (0.65)(0.83) + (0.35)(0.26)\) A1
\( = 0.6305\) (or 0.631) A1 N2
[4 marks]
evidence of using complement (M1)
e.g. \(1 – p\) , 0.3695
choosing a formula for conditional probability (M1)
e.g. \({\rm{P}}(H|W’) = \frac{{{\rm{P}}(W’ \cap H)}}{{{\rm{P}}(W’)}}\)
correct substitution
e.g. \(\frac{{(0.65)(0.17)}}{{0.3695}}\) \(\left( { = \frac{{0.1105}}{{0.3695}}} \right)\) A1
P(home) = 0.299 A1 N3
[4 marks]
Question
The weights of players in a sports league are normally distributed with a mean of \(76.6{\text{ kg}}\), (correct to three significant figures). It is known that \(80\% \) of the players have weights between \(68{\text{ kg}}\) and \(82{\text{ kg}}\). The probability that a player weighs less than \(68{\text{ kg}}\) is 0.05.
Find the probability that a player weighs more than \(82{\text{ kg}}\).
(i) Write down the standardized value, z, for \(68{\text{ kg}}\).
(ii) Hence, find the standard deviation of weights.
To take part in a tournament, a player’s weight must be within 1.5 standard deviations of the mean.
(i) Find the set of all possible weights of players that take part in the tournament.
(ii) A player is selected at random. Find the probability that the player takes part in the tournament.
Of the players in the league, \(25\% \) are women. Of the women, \(70\% \) take part in the tournament.
Given that a player selected at random takes part in the tournament, find the probability that the selected player is a woman.
Answer/Explanation
Markscheme
evidence of appropriate approach (M1)
e.g. \(1 – 0.85\) , diagram showing values in a normal curve
\({\rm{P}}(w \ge 82) = 0.15\) A1 N2
[2 marks]
(i) \(z = – 1.64\) A1 N1
(ii) evidence of appropriate approach (M1)
e.g. \( – 1.64 = \frac{{x – \mu }}{\sigma }\) , \(\frac{{68 – 76.6}}{\sigma }\)
correct substitution A1
e.g. \( – 1.64 = \frac{{68 – 76.6}}{\sigma }\)
\(\sigma = 5.23\) A1 N1
[4 marks]
(i) \(68.8 \le {\rm{weight}} \le 84.4\) A1A1A1 N3
Note: Award A1 for 68.8, A1 for 84.4, A1 for giving answer as an interval.
(ii) evidence of appropriate approach (M1)
e.g. \({\rm{P}}( – 1.5 \le z \le 1.5)\) , \({\rm{P}}(68.76 < y < 84.44)\)
\({\text{P(qualify)}} = 0.866\) A1 N2
[5 marks]
recognizing conditional probability (M1)
e.g. \({\rm{P}}(A|B) = \frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}}\)
\({\rm{P}}({\text{woman and qualify}}) = 0.25 \times 0.7\) (A1)
\({\rm{P}}({\rm{woman}}|{\rm{qualify}}) = \frac{{0.25 \times 0.7}}{{0.866}}\) A1
\({\rm{P}}({\rm{woman}}|{\rm{qualify}}) = 0.202\) A1
[4 marks]
Question
A factory makes lamps. The probability that a lamp is defective is 0.05. A random sample of 30 lamps is tested.
Find the probability that there is at least one defective lamp in the sample.
A factory makes lamps. The probability that a lamp is defective is 0.05. A random sample of 30 lamps is tested.
Given that there is at least one defective lamp in the sample, find the probability that there are at most two defective lamps.
Answer/Explanation
Markscheme
evidence of recognizing binomial (seen anywhere) (M1)
e.g. \({\rm{B}}(n{\text{, }}p)\), \({0.95^{30}}\)
finding \({\rm{P}}(X = 0) = 0.21463876\) (A1)
appropriate approach (M1)
e.g. complement, summing probabilities
\(0.785361\)
probability is \(0.785\) A1 N3
[4 marks]
identifying correct outcomes (seen anywhere) (A1)
e.g. \({\rm{P}}(X = 1) + {\rm{P}}(X = 2)\) , 1 or 2 defective, \(0.3389 \ldots + 0.2586 \ldots \)
recognizing conditional probability (seen anywhere) R1
e.g. \({\rm{P}}(A|B)\) , \({\rm{P}}(X \le 2|X \ge 1)\) , P(at most 2|at least 1)
appropriate approach involving conditional probability (M1)
e.g. \(\frac{{{\rm{P}}(X = 1) + {\rm{P}}(X = 2)}}{{{\rm{P}}(X \ge 1)}}\) , \(\frac{{0.3389 \ldots + 0.2586 \ldots }}{{0.785 \ldots }}\) , \(\frac{{1{\text{ or }}2}}{{0.785}}\)
\(0.760847\)
probability is \(0.761\) A1 N2
[4 marks]
Question
At a large school, students are required to learn at least one language, Spanish or French. It is known that \(75\% \) of the students learn Spanish, and \(40\% \) learn French.
Find the percentage of students who learn both Spanish and French.
At a large school, students are required to learn at least one language, Spanish or French. It is known that \(75\% \) of the students learn Spanish, and \(40\% \) learn French.
Find the percentage of students who learn Spanish, but not French.
At a large school, students are required to learn at least one language, Spanish or French. It is known that \(75\% \) of the students learn Spanish, and \(40\% \) learn French.
At this school, \(52\% \) of the students are girls, and \(85\% \) of the girls learn Spanish.
A student is chosen at random. Let G be the event that the student is a girl, and let S be the event that the student learns Spanish.
(i) Find \({\rm{P}}(G \cap S)\) .
(ii) Show that G and S are not independent.
At a large school, students are required to learn at least one language, Spanish or French. It is known that \(75\% \) of the students learn Spanish, and \(40\% \) learn French.
At this school, \(52\% \) of the students are girls, and \(85\% \) of the girls learn Spanish.
A boy is chosen at random. Find the probability that he learns Spanish.
Answer/Explanation
Markscheme
valid approach (M1)
e.g. Venn diagram with intersection, union formula,
\({\rm{P}}(S \cap F) = 0.75 + 0.40 – 1\)
\(15\) (accept \(15\% \)) A1 N2
[2 marks]
valid approach involving subtraction (M1)
e.g. Venn diagram, \(75 – 15\)
60 (accept \(60\% \)) A1 N2
[2 marks]
(i) valid approach (M1)
e.g. tree diagram, multiplying probabilities, \({\rm{P}}(S|G) \times {\rm{P(}}G{\rm{)}}\)
correct calculation (A1)
e.g. \(0.52 \times 0.85\)
\({\rm{P}}(G \cap S) = 0.442\) (exact) A1 N3
(ii) valid reasoning, with words, symbols or numbers (seen anywhere) R1
e.g. \({\rm{P(}}G{\rm{)}} \times {\rm{P}}(S) \ne {\rm{P}}(G \cap S)\) , \({\rm{P}}(S|G) \ne {\rm{P(}}S{\rm{)}}\) , not equal,
one correct value A1
e.g. \({\rm{P}}(G) \times {\rm{P}}(S) = 0.39\) , \({\rm{P}}(S|G) = 0.85\) , \(0.39 \ne 0.442\)
G and S are not independent AG N0
[5 marks]
METHOD 1
\(48\% \) are boys (seen anywhere) A1
e.g. \({\rm{P}}(B) = 0.48\)
appropriate approach (M1)
e.g. \({\text{P(girl and Spanish)}} + {\text{P(boy and Spanish)}} = {\text{P(Spanish)}}\)
correct approach to find P(boy and Spanish) (A1)
e.g. \({\rm{P(}}B \cap S{\rm{) = P(}}S{\rm{)}} – {\rm{P}}(G \cap S)\) , \({\rm{P(}}B \cap S{\rm{) = P(}}S|B) \times {\rm{P}}(B)\) , 0.308
correct substitution (A1)
e.g. \(0.442 + 0.48x = 0.75\) , \(0.48x = 0.308\)
correct manipulation (A1)
e.g. \({\rm{P}}(S|B) = \frac{{0.308}}{{0.48}}\)
\({\rm{P}}({\rm{Spanish}}|{\rm{boy}}) = 0.641666 \ldots \) , \(0.641\bar 6\)
\({\rm{P}}({\rm{Spanish}}|{\rm{boy}}) = 0.642\) \([0.641{\text{, }}0.642]\) A1 N3
[6 marks]
METHOD 2
\(48\% \) are boys (seen anywhere) A1
e.g. 0.48 used in tree diagram
appropriate approach (M1)
e.g. tree diagram
correctly labelled branches on tree diagram (A1)
e.g. first branches are boy/girl, second branches are Spanish/not Spanish
correct substitution (A1)
e.g. \(0.442 + 0.48x = 0.75\)
correct manipulation (A1)
e.g. \(0.48x = 0.308\) , \({\rm{P}}(S|B) = \frac{{0.308}}{{0.48}}\)
\({\rm{P}}({\rm{Spanish}}|{\rm{boy}}) = 0.641666 \ldots \) , \(0.641\bar 6\)
\({\rm{P}}({\rm{Spanish}}|{\rm{boy}}) = 0.642\) \([0.641{\text{, }}0.642]\)
[6 marks]
Question
A bag contains four gold balls and six silver balls.
Two balls are drawn at random from the bag, with replacement. Let \(X\) be the number of gold balls drawn from the bag.
Fourteen balls are drawn from the bag, with replacement.
(i) Find \({\rm{P}}(X = 0)\) .
(ii) Find \({\rm{P}}(X = 1)\) .
(iii) Hence, find \({\rm{E}}(X)\) .
Hence, find \({\rm{E}}(X)\) .
Find the probability that exactly five of the balls are gold.
Find the probability that at most five of the balls are gold.
Given that at most five of the balls are gold, find the probability that exactly five of the balls are gold. Give the answer correct to two decimal places.
Answer/Explanation
Markscheme
METHOD 1
(i) appropriate approach (M1)
eg \(\frac{6}{{10}} \times \frac{6}{{10}}\) , \(\frac{6}{{10}} \times \frac{5}{9}\) , \(\frac{6}{{10}} \times \frac{5}{{10}}\)
\({\rm{P}}(X = 0) = \frac{9}{{25}} = 0.36\) A1 N2
(ii) multiplying one pair of gold and silver probabilities (M1)
eg \(\frac{6}{{10}} \times \frac{4}{{10}}\) , \(\frac{6}{{10}} \times \frac{4}{9}\) , 0.24
adding the product of both pairs of gold and silver probabilities (M1)
eg \(\frac{6}{{10}} \times \frac{4}{{10}} \times 2\) , \(\frac{6}{{10}} \times \frac{4}{9} + \frac{4}{{10}} \times \frac{6}{9}\)
\({\rm{P}}(X = 1) = \frac{{12}}{{25}} = 0.48\) A1 N3
(iii)
\({\rm{P}}(X = 2) = 0.16\) (seen anywhere) (A1)
correct substitution into formula for \({\rm{E}}(X)\) (A1)
eg \(0 \times 0.36 + 1 \times 0.48 + 2 \times 0.16\) , \(0.48 + 0.32\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
METHOD 2
(i) evidence of recognizing binomial (may be seen in part (ii)) (M1)
eg \(X \sim {\rm{B}}(2,0.6)\) , \(\left( \begin{array}{l}
2\\
0
\end{array} \right){(0.4)^2}{(0.6)^0}\)
correct probability for use in binomial (A1)
eg \(p = 0.4\) , \(X \sim {\rm{B}}(2,0.4)\) , \(^2{C_0}{(0.4)^0}{(0.6)^2}\)
\({\rm{P}}(X = 0) = \frac{9}{{25}} = 0.36\) A1 N3
(ii) correct set up (A1)
eg \(_2{C_1}{(0.4)^1}{(0.6)^1}\)
\({\rm{P}}(X = 1) = \frac{{12}}{{25}} = 0.48\) A1 N2
(iii)
attempt to substitute into \(np\) (M1)
eg \(2 \times 0.6\)
correct substitution into \(np\) (A1)
eg \(2 \times 0.4\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
[8 marks]
METHOD 1
\({\rm{P}}(X = 2) = 0.16\) (seen anywhere) (A1)
correct substitution into formula for \({\rm{E}}(X)\) (A1)
eg \(0 \times 0.36 + 1 \times 0.48 + 2 \times 0.16\) , \(0.48 + 0.32\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
METHOD 2
attempt to substitute into \(np\) (M1)
eg \(2 \times 0.6\)
correct substitution into \(np\) (A1)
eg \(2 \times 0.4\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
[3 marks]
Let \(Y\) be the number of gold balls drawn from the bag.
evidence of recognizing binomial (seen anywhere) (M1)
eg \(_{14}{C_5}{(0.4)^5}{(0.6)^9}\) , \({\rm{B}}(14,0.4)\)
\({\rm{P}}(Y = 5) = 0.207\) A1 N2
[2 marks]
recognize need to find \({\rm{P}}(Y \le 5)\) (M1)
\({\rm{P}}(Y \le 5) = 0.486\) A1 N2
[2 marks]
Let \(Y\) be the number of gold balls drawn from the bag.
recognizing conditional probability (M1)
eg \({\rm{P}}(A|B)\) , \({\rm{P}}(Y = 5|Y \le 5)\) , \(\frac{{{\rm{P}}(Y = 5)}}{{{\rm{P}}(Y \le 5)}}\) , \(\frac{{0.207}}{{0.486}}\)
\({\rm{P}}(Y = 5|Y \le 5) = 0.42522518\) (A1)
\({\rm{P}}(Y = 5|Y \le 5) = 0.43\) (to \(2\) dp) A1 N2
[3 marks]
Question
Samantha goes to school five days a week. When it rains, the probability that she goes to school by bus is 0.5. When it does not rain, the probability that she goes to school by bus is 0.3. The probability that it rains on any given day is 0.2.
On a randomly selected school day, find the probability that Samantha goes to school by bus.
Given that Samantha went to school by bus on Monday, find the probability that it was raining.
In a randomly chosen school week, find the probability that Samantha goes to school by bus on exactly three days.
After \(n\) school days, the probability that Samantha goes to school by bus at least once is greater than \(0.95\). Find the smallest value of \(n\).
Answer/Explanation
Markscheme
appropriate approach (M1)
eg \({\text{P}}(R \cap B) + {\text{P}}(R’ \cap B)\), tree diagram,
one correct multiplication (A1)
eg \(0.2 \times 0.5,{\text{ }}0.24\)
correct working (A1)
eg \(0.2 \times 0.5 + 0.8 \times 0.3,{\text{ }}0.1 + 0.24\)
\({\text{P(bus)}} = 0.34 {\text{(exact)}}\) A1 N3
[4 marks]
recognizing conditional probability (R1)
eg \({\text{P}}(A|B) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\)
correct working A1
eg \(\frac{{0.2 \times 0.5}}{{0.34}}\)
\({\text{P}}(R|B) = \frac{5}{{17}},{\text{ }}0.294\) A1 N2
[3 marks]
recognizing binomial probability (R1)
eg \(X \sim {\text{B}}(n,{\text{ }}p)\), \(\left( \begin{array}{c}5\\3\end{array} \right)\) \({(0.34)^3},{\text{ }}{(0.34)^3}{(1 – 0.34)^2}\)
\({\text{P}}(X = 3) = 0.171\) A1 N2
[2 marks]
METHOD 1
evidence of using complement (seen anywhere) (M1)
eg \(1 – {\text{P (none), }}1 – 0.95\)
valid approach (M1)
eg \(1 – {\text{P (none)}} > 0.95,{\text{ P (none)}} < 0.05,{\text{ }}1 – {\text{P (none)}} = 0.95\)
correct inequality (accept equation) A1
eg \(1 – {(0.66)^n} > 0.95,{\text{ }}{(0.66)^n} = 0.05\)
\(n > 7.209{\text{ (accept }}n = 7.209{\text{)}}\) (A1)
\(n = 8\) A1 N3
METHOD 2
valid approach using guess and check/trial and error (M1)
eg finding \({\text{P}}(X \geqslant 1)\) for various values of n
seeing the “cross over” values for the probabilities A1A1
\(n = 7,{\text{ P}}(X \geqslant 1) = 0.9454,{\text{ }}n = 8,{\text{ P}}(X \geqslant 1) = 0.939\)
recognising \(0.9639 > 0.95\) (R1)
\(n = 8\) A1 N3
[5 marks]
Question
A forest has a large number of tall trees. The heights of the trees are normally distributed with a mean of \(53\) metres and a standard deviation of \(8\) metres. Trees are classified as giant trees if they are more than \(60\) metres tall.
A tree is selected at random from the forest.
Find the probability that this tree is a giant.
A tree is selected at random from the forest.
Given that this tree is a giant, find the probability that it is taller than \(70\) metres.
Two trees are selected at random. Find the probability that they are both giants.
\(100\) trees are selected at random.
Find the expected number of these trees that are giants.
\(100\) trees are selected at random.
Find the probability that at least \(25\) of these trees are giants.
Answer/Explanation
Markscheme
valid approach (M1)
eg \({\text{P}}(G) = {\text{P}}(H > 60,{\text{ }}z = 0.875,{\text{ P}}(H > 60) = 1 – 0.809,{\text{ N}}\left( {53, {8^2}} \right)\)
\(0.190786\)
\({\text{P}}(G) = 0.191\) A1 N2
[3 marks]
finding \({\text{P}}(H > 70) = 0.01679\) (seen anywhere) (A1)
recognizing conditional probability (R1)
eg \({\text{P}}(A\left| {B),{\text{ P}}(H > 70\left| {H > 60)} \right.} \right.\)
correct working (A1)
eg \(\frac{{0.01679}}{{0.191}}\)
\(0.0880209\)
\({\text{P}}(X > 70\left| {G) = 0.0880} \right.\) A1 N3
[6 marks]
attempt to square their \({\text{P}}(G)\) (M1)
eg \({0.191^2}\)
\(0.0363996\)
\({\text{P}}({\text{both }}G) = 0.0364\) A1 N2
[2 marks]
correct substitution into formula for \({\text{E}}(X)\) (A1)
eg \(100(0.191)\)
\({\text{E}}(G) = 19.1{\text{ }}[19.0,{\text{ }}19.1]\) A1 N2
[3 marks]
recognizing binomial probability (may be seen in part (c)(i)) (R1)
eg \(X \sim {\text{B}}(n,{\text{ }}p)\)
valid approach (seen anywhere) (M1)
eg \({\text{P}}(X \geqslant 25) = 1 – {\text{P}}(X \leqslant 24),{\text{ }}1 – {\text{P}}(X < a)\)
correct working (A1)
eg \({\text{P}}(X \leqslant 24) = 0.913 \ldots ,{\text{ }}1 – 0.913 \ldots \)
\(0.0869002\)
\({\text{P}}(X \geqslant 25) = 0.0869\) A1 N2
[3 marks]
Question
The following cumulative frequency graph shows the monthly income, \(I\) dollars, of \(2000\) families.
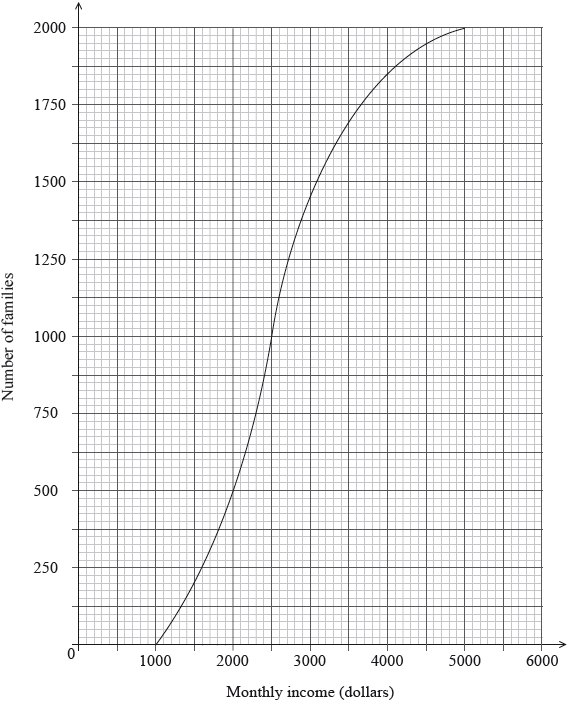
Find the median monthly income.
(i) Write down the number of families who have a monthly income of \(2000\) dollars or less.
(ii) Find the number of families who have a monthly income of more than \(4000\) dollars.
The \(2000\) families live in two different types of housing. The following table gives information about the number of families living in each type of housing and their monthly income \(I\).

Find the value of \(p\).
A family is chosen at random.
(i) Find the probability that this family lives in an apartment.
(ii) Find the probability that this family lives in an apartment, given that its monthly income is greater than \(4000\) dollars.
Estimate the mean monthly income for families living in a villa.
Answer/Explanation
Markscheme
recognizing that the median is at half the total frequency (M1)
eg\(\;\;\;\)\(\frac{{2000}}{2}\)
\(m = 2500{\text{ (dollars)}}\) A1 N2
[2 marks]
(i) \(500\) families have a monthly income less than \(2000\) A1 N1
(ii) correct cumulative frequency, \(1850\) (A1)
subtracting their cumulative frequency from \(2000\) (M1)
eg\(\;\;\;\)\(2000 – 1850\)
\(150\) families have a monthly income of more than \(4000\) dollars A1 N2
Note: If working shown, award M1A1A1 for \(128{\rm{ }} + {\rm{ }}22{\rm{ }} = {\rm{ }}150\), using the table.
[4 marks]
correct calculation (A1)
eg\(\;\;\;\)\(2000 – (436 + 64 + 765 + 28 + 122),{\text{ }}1850 – 500 – 765\) (A1)
\(p = 585\) A1 N2
[2 marks]
(i) correct working (A1)
eg\(\;\;\;\)\(436 + 765 + 28\)
\(0.6145\;\;\;\)(exact) A1 N2
\(\frac{{1229}}{{2000}},{\text{ }}0.615{\text{ }}[0.614,{\text{ }}0.615]\)
(ii) correct working/probability for number of families (A1)
eg\(\;\;\;\)\(122 + 28,{\text{ }}\frac{{150}}{{2000}},{\text{ 0.075}}\)
\(0.186666\)
\(\frac{{28}}{{150}}\;\;\;\left( { = \frac{{14}}{{75}}} \right),{\text{ }}0.187{\text{ }}[0.186,{\text{ }}0.187]\) A1 N2
[4 marks]
evidence of using correct mid-interval values (\(1500,{\rm{ }}3000,{\rm{ }}4500\)) (A1)
attempt to substitute into \(\frac{{\sum {fx} }}{{\sum f }}\) (M1)
eg\(\;\;\;\)\(\frac{{1500 \times 64 + 3000 \times p + 4500 \times 122}}{{64 + 585 + 122}}\)
\(3112.84\)
\(3110{\text{ }}[3110,{\text{ }}3120]{\text{ (dollars)}}\) A1 N2
[3 marks]
Total [15 marks]
Question
The weights of fish in a lake are normally distributed with a mean of \(760\) g and standard deviation \(\sigma \). It is known that \(78.87\% \) of the fish have weights between \(705\) g and \(815\) g.
(i) Write down the probability that a fish weighs more than \(760\) g.
(ii) Find the probability that a fish weighs less than \(815\) g.
(i) Write down the standardized value for \(815\) g.
(ii) Hence or otherwise, find \(\sigma \).
A fishing contest takes place in the lake. Small fish, called tiddlers, are thrown back into the lake. The maximum weight of a tiddler is \(1.5\) standard deviations below the mean.
Find the maximum weight of a tiddler.
A fish is caught at random. Find the probability that it is a tiddler.
\(25\% \) of the fish in the lake are salmon. \(10\% \) of the salmon are tiddlers. Given that a fish caught at random is a tiddler, find the probability that it is a salmon.
Answer/Explanation
Markscheme
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
(i) \({\text{P}}(X > 760) = 0.5{\text{ (exact), }}[0.499,{\text{ }}0.500]{\text{ }}\) A1 N1
(ii) evidence of valid approach (M1)
recognising symmetry, \(\frac{{0.7887}}{2},{\text{ }}1 – {\text{P}}(W < 815),{\text{ }}\frac{{21.13}}{2} + 78.87\% \)
correct working (A1)
eg\(\;\;\;\)\(0.5 + 0.39435,{\text{ }}1 – 0.10565,\)
\(0.89435{\text{ (exact)}},{\text{ }}0.894{\text{ }}[0.894,{\text{ }}0.895]\) A1 N2
[4 marks]
(i) \(1.24999\) A1 N1
\(z = 1.25{\text{ }}[1.24,{\text{ }}1.25]\)
(ii) evidence of appropriate approach (M1)
eg\(\;\;\;\)\(\sigma = \frac{{x – \mu }}{{1.25}},{\text{ }}\frac{{815 – 760}}{\sigma }\)
correct substitution (A1)
eg\(\;\;\;\)\(1.25 = \frac{{815 – 760}}{\sigma },{\text{ }}\frac{{815 – 760}}{{1.24999}}\)
\(44.0003\)
\(\sigma = 44.0{\text{ }}[44.0,{\text{ }}44.1]{\text{ (g)}}\) A1 N2
[4 marks]
correct working (A1)
eg\(\;\;\;\)\(760 – 1.5 \times 44\)
\(693.999\)
\(694{\text{ }}[693,{\text{ }}694]{\text{ (g)}}\) A1 N2
[2 marks]
\(0.0668056\)
\({\text{P}}(X < 694) = 0.0668{\text{ }}[0.0668,{\text{ }}0.0669]\) A2 N2
[2 marks]
recognizing conditional probability (seen anywhere) (M1)
eg\(\;\;\;\)\({\text{P}}({\text{A}}|{\text{B}}),{\text{ }}\frac{{0.025}}{{0.0668}}\)
appropriate approach involving conditional probability (M1)
eg\(\;\;\;\)\({\text{P}}(S|T) = \frac{{{\text{P}}(S{\text{ and }}T)}}{{{\text{P}}(T)}}\),
correct working
eg\(\;\;\;\)P (salmon and tiddler) \( = 0.25 \times 0.1,{\text{ }}\frac{{0.25 \times 0.1}}{{0.0668}}\) (A1)
\(0.374220\)
\(0.374{\text{ }}[0.374,{\text{ }}0.375]\) A1 N2
[4 marks]
Total [16 marks]
Question
A company makes containers of yogurt. The volume of yogurt in the containers is normally distributed with a mean of \(260\) ml and standard deviation of \(6\) ml.
A container which contains less than \(250\) ml of yogurt is underfilled.
A container is chosen at random. Find the probability that it is underfilled.
The company decides that the probability of a container being underfilled should be reduced to \(0.02\). It decreases the standard deviation to \(\sigma \) and leaves the mean unchanged.
Find \(\sigma \).
The company changes to the new standard deviation, \(\sigma \), and leaves the mean unchanged.
A container is chosen at random for inspection. It passes inspection if its volume of yogurt is between \(250\) and \(271\) ml.
(i) Find the probability that it passes inspection.
(ii) Given that the container is not underfilled, find the probability that it passes inspection.
A sample of \(50\) containers is chosen at random. Find the probability that \(48\) or more of the containers pass inspection.
Answer/Explanation
Markscheme
\(0.0477903\)
probability \( = 0.0478\) A2 N2
[2 marks]
\({\text{P}}({\text{volume}} < 250) = 0.02\) (M1)
\(z = – 2.05374\;\;\;\)(may be seen in equation) A1
attempt to set up equation with \(z\) (M1)
eg\(\;\;\;\frac{{\mu – 260}}{\sigma } = z,{\text{ }}260 – 2.05(\sigma ) = 250\)
\(4.86914\)
\(\sigma = 4.87{\text{ (ml)}}\) A1 N3
[4 marks]
(i) \(0.968062\)
\({\text{P}}(250 < {\text{Vol}} < 271) = 0.968\) A2 N2
(ii) recognizing conditional probability (seen anywhere, including in correct working) R1
eg\(\;\;\;{\text{P}}(A|B),{\text{ }}\frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}},{\text{ P}}(A \cap B) = {\text{P}}(A|B){\text{P}}(B)\)
correct value or expression for \(P\) (not underfilled) (A1)
eg\(\;\;\;0.98,1 – 0.02,{\text{ }}1 – {\text{P}}(X < 250)\)
probability \( = \frac{{0.968}}{{0.98}}\) A1
\(0.987818\)
probability \( = 0.988\) A1 N2
[6 marks]
METHOD 1
evidence of recognizing binomial distribution (seen anywhere) (M1)
eg\(\;\;\;X\;\;\;{\text{B}}(50,{\text{ }}0.968),{\text{ binomial cdf, }}p = 0.968,{\text{ }}r = 47\)
\({\text{P}}(X \le 47\)) = 0.214106\) (A1)
evidence of using complement (M1)
eg\(\;\;\;1 – {\text{P}}(X \le 47\))
\(0.785894\)
probability \( = 0.786\) A1 N3
METHOD 2
evidence of recognizing binomial distribution (seen anywhere) (M1)
eg\(\;\;\;X\;\;\;{\text{B}}(50,{\text{ }}0.968),{\text{ binomial cdf, }}p = 0.968,{\text{ }}r = 47\)
\({\text{P(not pass)}} = 1 – {\text{P(pass)}} = 0.0319378\) (A1)
evidence of attempt to find \(P\) (\(2\) or fewer fail) (M1)
eg\(\;\;\;\)\(0\), \(1\), or \(2\) not pass, \({\text{B}}(50,{\text{ }}2)\)
\(0.785894\)
probability \( = 0.786\) A1 N3
METHOD 3
evidence of recognizing binomial distribution (seen anywhere) (M1)
eg\(\;\;\;X\;\;\;{\text{B}}(50,{\text{ }}0.968),{\text{ binomial cdf, }}p = 0.968,{\text{ }}r = 47\)
evidence of summing probabilities (M1)
eg\(\;\;\;{\text{P}}(X = 48) + {\text{P}}(X = 49) + {\text{P}}(X = 50)\)
correct working
eg\(\;\;\;0.263088 + 0.325488 + 0.197317\) (A1)
\(0.785894\)
probability \( = 0.786\) A1 N3
[4 marks]
Total [16 marks]
Question
Let \(C\) and \(D\) be independent events, with \({\text{P}}(C) = 2k\) and \({\text{P}}(D) = 3{k^2}\), where \(0 < k < 0.5\).
Write down an expression for \({\text{P}}(C \cap D)\) in terms of \(k\).
Given that \({\text{P}}(C \cap D) = 0.162\) find \(k\).
Find \({\text{P}}(C’|D)\).
Answer/Explanation
Markscheme
\({\text{P}}(C \cap D) = 2k \times 3{k^2}\) (A1)
\({\text{P}}(C \cap D) = 6{k^3}\) A1 N2
[2 marks]
their correct equation (A1)
eg\(\;\;\;2k \times 3{k^2} = 0.162,{\text{ }}6{k^3} = 0.162\)
\(k = 0.3\) A1 N2
METHOD 1
finding their \({\text{P}}(C’ \cap D)\) (seen anywhere) (A1)
eg \(0.4 \times 0.27,0.27 – 0.162,0.108\)
correct substitution into conditional probability formula (A1)
eg\(\;\;\;{\text{P}}(C’|D) = \frac{{{\text{P}}(C’ \cap D)}}{{0.27}},{\text{ }}\frac{{(1 – 2k)(3{k^2})}}{{3{k^2}}}\)
\({\text{P}}(C’|D) = 0.4\) A1 N2
METHOD 2
recognizing \({\text{P}}(C’|D) = {\text{P}}(C’)\) A1
finding their \({\text{P}}(C’) = 1 – {\text{P}}(C)\) (only if first line seen) (A1)
eg\(\;\;\;1 – 2k,{\text{ }}1 – 0.6\)
\({\text{P}}(C’|D) = 0.4\) A1 N2
[3 marks]
Total [7 marks]
Question
The masses of watermelons grown on a farm are normally distributed with a mean of \(10\) kg.
The watermelons are classified as small, medium or large.
A watermelon is small if its mass is less than \(4\) kg. Five percent of the watermelons are classified as small.
Find the standard deviation of the masses of the watermelons.
The following table shows the percentages of small, medium and large watermelons grown on the farm.

A watermelon is large if its mass is greater than \(w\) kg.
Find the value of \(w\).
All the medium and large watermelons are delivered to a grocer.
The grocer selects a watermelon at random from this delivery. Find the probability that it is medium.
All the medium and large watermelons are delivered to a grocer.
The grocer sells all the medium watermelons for $1.75 each, and all the large watermelons for $3.00 each. His costs on this delivery are $300, and his total profit is $150. Find the number of watermelons in the delivery.
Answer/Explanation
Markscheme
finding standardized value for 4 kg (seen anywhere) (A1)
eg\(\;\;\;z = – 1.64485\)
attempt to standardize (M1)
eg\(\;\;\;\sigma = \frac{{x – \mu }}{z},{\text{ }}\frac{{4 – 10}}{\sigma }\)
correct substitution (A1)
eg\(\;\;\; – 1.64 = \frac{{4 – 10}}{\sigma },{\text{ }}\frac{{4 – 10}}{{ – 1.64}}\)
\(\sigma = 3.64774\)
\(\sigma = 3.65\) A1 N2
[4 marks]
valid approach (M1)
eg\(\;\;\;1 – p,{\text{ 0.62, }}\frac{{w – 10}}{{3.65}} = 0.305\)
\(w = 11.1143\)
\(w = 11.1\) A1 N2
[2 marks]
attempt to restrict melon population (M1)
eg\(\;\;\;\)\(95\% \) are delivered, \({\text{P}}({\text{medium}}|{\text{delivered}}),{\text{ }}57 + 38\)
correct probability for medium watermelons (A1)
eg\(\;\;\;\frac{{0.57}}{{0.95}}\)
\(\frac{{57}}{{95}},{\text{ }}0.6,{\text{ }}60\% \) A1 N3
[3 marks]
proportion of large watermelons (seen anywhere) (A1)
eg\(\;\;\;{\text{P(large)}} = 0.4,{\text{ }}40\% \)
correct approach to find total sales (seen anywhere) (A1)
eg\(\;\;\;150 = {\text{sales}} – 300,{\text{ total sales}} = \$ 450\)
correct expression (A1)
eg\(\;\;\;1.75(0.6x) + 3(0.4x),{\text{ }}1.75(0.6) + 3(0.4)\)
evidence of correct working (A1)
eg\(\;\;\;1.75(0.6x) + 3(0.4x) = 450,{\text{ }}2.25x = 450\)
200 watermelons in the delivery A1 N2
Notes: If candidate answers 0.57 in part (c), the FT values are \({\text{P(large)}} = 0.43\) and 197 watermelons. Award FT marks if working shown.
Award N0 for 197.
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
Question
A factory has two machines, A and B. The number of breakdowns of each machine is independent from day to day.
Let \(A\) be the number of breakdowns of Machine A on any given day. The probability distribution for \(A\) can be modelled by the following table.

Let \(B\) be the number of breakdowns of Machine B on any given day. The probability distribution for \(B\) can be modelled by the following table.

On Tuesday, the factory uses both Machine A and Machine B. The variables \(A\) and \(B\) are independent.
Find \(k\).
(i) A day is chosen at random. Write down the probability that Machine A has no breakdowns.
(ii) Five days are chosen at random. Find the probability that Machine A has no breakdowns on exactly four of these days.
Find \({\text{E}}(B)\).
(i) Find the probability that there are exactly two breakdowns on Tuesday.
(ii) Given that there are exactly two breakdowns on Tuesday, find the probability that both breakdowns are of Machine A.
Answer/Explanation
Markscheme
evidence of summing to 1 (M1)
eg\(\,\,\,\,\,\)\(0.55 + 0.3 + 0.1 + k = 1\)
\(k = 0.05{\text{ (exact)}}\) A1 N2
[2 marks]
(i) 0.55 A1 N1
(ii) recognizing binomial probability (M1)
eg\(\,\,\,\,\,\)\(X:{\text{ }}B(n,{\text{ }}p),{\text{ }}\left( {\begin{array}{*{20}{c}} 5 \\ 4 \end{array}} \right),{\text{ }}{(0.55)^4}(1 – 0.55),{\text{ }}\left( {\begin{array}{*{20}{c}} n \\ r \end{array}} \right){p^r}{q^{n – r}}\)
\(P(X = 4) = 0.205889\)
\(P(X = 4) = 0.206\) A1 N2
[3 marks]
correct substitution into formula for \({\text{E}}(X)\) (A1)
eg\(\,\,\,\,\,\)\(0.2 + (2 \times 0.08) + (3 \times 0.02)\)
\({\text{E}}(B) = 0.42{\text{ (exact)}}\) A1 N2
[2 marks]
(i) valid attempt to find one possible way of having 2 breakdowns (M1)
eg\(\,\,\,\,\,\)\(2A,{\text{ }}2B,{\text{ }}1A\) and \(1B\), tree diagram
one correct calculation for 1 way (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\(0.1 \times 0.7,{\text{ }}0.55 \times 0.08,{\text{ }}0.3 \times 0.2\)
recognizing there are 3 ways of having 2 breakdowns (M1)
eg\(\,\,\,\,\,\)A twice or B twice or one breakdown each
correct working (A1)
eg\(\,\,\,\,\,\)\((0.1 \times 0.7) + (0.55 \times 0.08) + (0.3 \times 0.2)\)
\({\text{P(2 breakdowns)}} = 0.174{\text{ (exact)}}\) A1 N3
(ii) recognizing conditional probability (M1)
eg\(\,\,\,\,\,\)\({\text{P}}(A|B),{\text{ P}}(2A|{\text{2breakdowns}})\)
correct working (A1)
eg\(\,\,\,\,\,\)\(\frac{{0.1 \times 0.7}}{{0.174}}\)
\({\text{P}}(A = 2|{\text{two breakdowns}}) = 0.402298\)
\({\text{P}}(A = 2|{\text{two breakdowns}}) = 0.402\) A1 N2
[8 marks]
Question
A random variable \(X\) is normally distributed with mean, \(\mu \). In the following diagram, the shaded region between 9 and \(\mu \) represents 30% of the distribution.
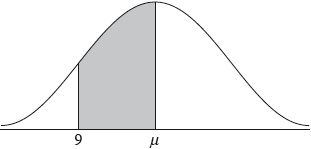
The standard deviation of \(X\) is 2.1.
The random variable \(Y\) is normally distributed with mean \(\lambda \) and standard deviation 3.5. The events \(X > 9\) and \(Y > 9\) are independent, and \(P\left( {(X > 9) \cap (Y > 9)} \right) = 0.4\).
Find \({\text{P}}(X < 9)\).
Find the value of \(\mu \).
Find \(\lambda \).
Given that \(Y > 9\), find \({\text{P}}(Y < 13)\).
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\({\text{P}}(X < \mu ) = 0.5,{\text{ }}0.5 – 0.3\)
\({\text{P}}(X < 9) = 0.2\) (exact) A1 N2
[2 marks]
\(z = – 0.841621\) (may be seen in equation) (A1)
valid attempt to set up an equation with their \(z\) (M1)
eg\(\,\,\,\,\,\)\( – 0.842 = \frac{{\mu – X}}{\sigma },{\text{ }} – 0.842 = \frac{{X – \mu }}{\sigma },{\text{ }}z = \frac{{9 – \mu }}{{2.1}}\)
10.7674
\(\mu = 10.8\) A1 N3
[3 marks]
\({\text{P}}(X > 9) = 0.8\) (seen anywhere) (A1)
valid approach (M1)
eg\(\,\,\,\,\,\)\({\text{P}}(A) \times {\text{P}}(B)\)
correct equation (A1)
eg\(\,\,\,\,\,\)\(0.8 \times {\text{P}}(Y > 9) = 0.4\)
\({\text{P}}(Y > 9) = 0.5\) A1
\(\lambda = 9\) A1 N3
[5 marks]
finding \({\text{P}}(9 < Y < 13) = 0.373450\) (seen anywhere) (A2)
recognizing conditional probability (M1)
eg\(\,\,\,\,\,\)\({\text{P}}(A|B),{\text{ P}}(Y < 13|Y > 9)\)
correct working (A1)
eg\(\,\,\,\,\,\)\(\frac{{{\text{0.373}}}}{{0.5}}\)
0.746901
0.747 A1 N3
[5 marks]
Question
A discrete random variable \(X\) has the following probability distribution.

Find the value of \(k\).
Write down \({\text{P}}(X = 2)\).
Find \({\text{P}}(X = 2|X > 0)\).
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)total probability = 1
correct equation (A1)
eg\(\,\,\,\,\,\)\(0.475 + 2{k^2} + \frac{k}{{10}} + 6{k^2} = 1,{\text{ }}8{k^2} + 0.1k – 0.525 = 0\)
\(k = 0.25\) A2 N3
[4 marks]
\({\text{P}}(X = 2) = 0.025\) A1 N1
[1 mark]
valid approach for finding \({\text{P}}(X > 0)\) (M1)
eg\(\,\,\,\,\,\)\(1 – 0.475,{\text{ }}2({0.25^2}) + 0.025 + 6({0.25^2}),{\text{ }}1 – {\text{P}}(X = 0),{\text{ }}2{k^2} + \frac{k}{{10}} + 6{k^2}\)
correct substitution into formula for conditional probability (A1)
eg\(\,\,\,\,\,\)\(\frac{{0.025}}{{1 – 0.475}},{\text{ }}\frac{{0.025}}{{0.525}}\)
0.0476190
\({\text{P}}(X = 2|X > 0) = \frac{1}{{21}}\) (exact), 0.0476 A1 N2
[3 marks]
Question
Two events A and B are such that P(A) = 0.62 and P\(\left( {A \cap B} \right)\) = 0.18.
Find P(A ∩ B′ ).
Given that P((A ∪ B)′ ) = 0.19, find P(A | B′ ).
Answer/Explanation
Markscheme
valid approach
eg Venn diagram, P(A) − P (A ∩ B), 0.62 − 0.18 (M1)
P(A ∩ B’ ) = 0.44 A1 N2
[2 marks]
valid approach to find either P(B′ ) or P(B) (M1)
eg (seen anywhere), 1 − P(A ∩ B′ ) − P((A ∪ B)′ )
correct calculation for P(B′ ) or P(B) (A1)
eg 0.44 + 0.19, 0.81 − 0.62 + 0.18
correct substitution into \(\frac{{{\text{P}}\left( {A \cap B’} \right)}}{{{\text{P}}\left( {B’} \right)}}\) (A1)
eg \(\frac{{0.44}}{{0.19 + 0.44}},\,\,\frac{{0.44}}{{1 – 0.37}}\)
0.698412
P(A | B′ ) = \(\frac{{44}}{{63}}\) (exact), 0.698 A1 N3
[4 marks]

