Question
A four-sided die has three blue faces and one red face. The die is rolled.
Let B be the event a blue face lands down, and R be the event a red face lands down.
Write down
(i) P(B);
(ii) P(R).
If the blue face lands down, the die is not rolled again. If the red face lands down, the die is rolled once again. This is represented by the following tree diagram, where p, s, t are probabilities.
Find the value of p, of s and of t.
Guiseppi plays a game where he rolls the die. If a blue face lands down, he scores 2 and is finished. If the red face lands down, he scores 1 and rolls one more time. Let X be the total score obtained.
(i) Show that \({\text{P}}(X = 3) = \frac{3}{{16}}\) .
(ii) Find \({\text{P}}(X = 2)\) .
(i) Construct a probability distribution table for X.
(ii) Calculate the expected value of X.
If the total score is 3, Guiseppi wins \(\$ 10\). If the total score is 2, Guiseppi gets nothing.
Guiseppi plays the game twice. Find the probability that he wins exactly \(\$ 10\).
Answer/Explanation
Markscheme
(i) P(B) \( = \frac{3}{4}\) A1 N1
(ii) P(R) \( = \frac{1}{4}\) A1 N1
[2 marks]
\(p = \frac{3}{4}\) A1 N1
\(s = \frac{1}{4}\), \(t = \frac{3}{4}\) A1 N1
[2 marks]
(i) \({\text{P}}(X = 3)\)
\( = {\text{P (getting 1 and 2)}} = \frac{1}{4} \times \frac{3}{4}\) A1
\( = \frac{3}{{16}}\) AG N0
(ii) \({\text{P}}(X = 2) = \frac{1}{4} \times \frac{1}{4} + \frac{3}{4}{\text{ }}\left( {{\text{or }}1 – \frac{3}{{16}}} \right)\) (A1)
\( = \frac{{13}}{{16}}\) A1 N2
[3 marks]
(i)
A2 N2
(ii) evidence of using \({\text{E}}(X) = \sum{x{\text{P}}(X = x)} \) (M1)
\({\text{E}}(X) = 2\left( {\frac{{13}}{{16}}} \right) + 3\left( {\frac{3}{{16}}} \right)\) (A1)
\( = \frac{{35}}{{16}}{\text{ }}\left( { = 2\frac{3}{{16}}} \right)\) A1 N2
[5 marks]
win \(\$ 10 \Rightarrow \) scores 3 one time, 2 other time (M1)
\({\text{P}}(3) \times {\text{P}}(2) = \frac{{13}}{{16}} \times \frac{3}{{16}}\) (seen anywhere) A1
evidence of recognising there are different ways of winning \(\$ 10\) (M1)
e.g. \({\text{P}}(3) \times {\text{P}}(2) + {\text{P}}(2) \times {\text{P}}(3)\) , \(2\left( {\frac{{13}}{{16}} \times \frac{3}{{16}}} \right)\) , \(\frac{{36}}{{256}} + \frac{3}{{256}} + \frac{{36}}{{256}} + \frac{3}{{256}}\)
\({\text{P(win }}\$ 10) = \frac{{78}}{{256}}{\text{ }}\left( { = \frac{{39}}{{128}}} \right)\) A1 N3
[4 marks]
Question
Let A and B be independent events, where \({\text{P}}(A) = 0.6\) and \({\text{P}}(B) = x\) .
Write down an expression for \({\text{P}}(A \cap B)\) .
Given that \({\text{P}}(A \cup B) = 0.8\) ,
(i) find x ;
(ii) find \({\text{P}}(A \cap B)\) .
Hence, explain why A and B are not mutually exclusive.
Answer/Explanation
Markscheme
\({\text{P}}(A \cap B) = {\text{P}}(A) \times {\text{P}}(B)( = 0.6x)\) A1 N1
[1 mark]
(i) evidence of using \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
correct substitution A1
e.g. \(0.8 = 0.6 + x – 0.6x\) , \(0.2 = 0.4x\)
\(x = 0.5\) A1 N2
(ii) \({\text{P}}(A \cap B) = 0.3\) A1 N1
[4 marks]
valid reason, with reference to \({\text{P(}}A \cap B)\) R1 N1
e.g. \({\text{P(}}A \cap B) \ne 0\)
[1 mark]
Question
In a class of 100 boys, 55 boys play football and 75 boys play rugby. Each boy must play at least one sport from football and rugby.
(i) Find the number of boys who play both sports.
(ii) Write down the number of boys who play only rugby.
One boy is selected at random.
(i) Find the probability that he plays only one sport.
(ii) Given that the boy selected plays only one sport, find the probability that he plays rugby.
Let A be the event that a boy plays football and B be the event that a boy plays rugby.
Explain why A and B are not mutually exclusive.
Show that A and B are not independent.
Answer/Explanation
Markscheme
(i) evidence of substituting into \(n(A \cup B) = n(A) + n(B) – n(A \cap B)\) (M1)
e.g. \(75 + 55 – 100\) , Venn diagram
30 A1 N2
(ii) 45 A1 N1
[3 marks]
(i) METHOD 1
evidence of using complement, Venn diagram (M1)
e.g. \(1 – p\) , \(100 – 30\)
\(\frac{{70}}{{100}}\) \(\left( { = \frac{7}{{10}}} \right)\) A1 N2
METHOD 2
attempt to find P(only one sport) , Venn diagram (M1)
e.g. \(\frac{{25}}{{100}} + \frac{{45}}{{100}}\)
\(\frac{{70}}{{100}}\) \(\left( { = \frac{7}{{10}}} \right)\) A1 N2
(ii) \(\frac{{45}}{{70}}\) \(\left( { = \frac{9}{{14}}} \right)\) A2 N2
[4 marks]
valid reason in words or symbols (R1)
e.g. \({\rm{P}}(A \cap B) = 0\) if mutually exclusive, \({\rm{P}}(A \cap B) \ne 0\) if not mutually exclusive
correct statement in words or symbols A1 N2
e.g. \({\rm{P}}(A \cap B) = 0.3\) , \({\rm{P}}(A \cup B) \ne {\rm{P}}(A) + {\rm{P}}(B)\) , \({\rm{P}}(A) + {\rm{P}}(B) > 1\) , some students play both sports, sets intersect
[2 marks]
valid reason for independence (R1)
e.g. \({\rm{P}}(A \cap B) = {\rm{P}}(A) \times {\rm{P}}(B)\) , \({\rm{P}}(B|A) = {\rm{P}}(B)\)
correct substitution A1A1 N3
e.g. \(\frac{{30}}{{100}} \ne \frac{{75}}{{100}} \times \frac{{55}}{{100}}\) , \(\frac{{30}}{{55}} \ne \frac{{75}}{{100}}\)
[3 marks]
Question
Consider the events A and B, where \({\rm{P}}(A) = 0.5\) , \({\rm{P}}(B) = 0.7\) and \({\rm{P}}(A \cap B) = 0.3\) .
The Venn diagram below shows the events A and B, and the probabilities p, q and r.
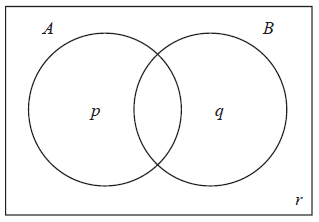
Write down the value of
(i) p ;
(ii) q ;
(iii) r.
Find the value of \({\rm{P}}(A|B’)\) .
Hence, or otherwise, show that the events A and B are not independent.
Answer/Explanation
Markscheme
(i) \(p = 0.2\) A1 N1
(ii) \(q = 0.4\) A1 N1
(iii) \(r = 0.1\) A1 N1
[3 marks]
\({\rm{P}}(A|B’) = \frac{2}{3}\) A2 N2
Note: Award A1 for an unfinished answer such as \(\frac{{0.2}}{{0.3}}\) .
[2 marks]
valid reason R1
e.g. \(\frac{2}{3} \ne 0.5\) , \(0.35 \ne 0.3\)
thus, A and B are not independent AG N0
[1 mark]
Question
In a class of 21 students, 12 own a laptop, 10 own a tablet, and 3 own neither.
The following Venn diagram shows the events “own a laptop” and “own a tablet”.
The values \(p\), \(q\), \(r\) and \(s\) represent numbers of students.
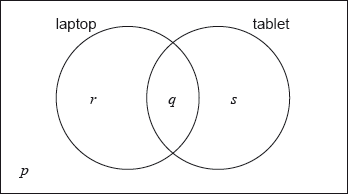
A student is selected at random from the class.
Two students are randomly selected from the class. Let \(L\) be the event a “student owns a laptop”.
(i) Write down the value of \(p\).
(ii) Find the value of \(q\).
(iii) Write down the value of \(r\) and of \(s\).
(i) Write down the probability that this student owns a laptop.
(ii) Find the probability that this student owns a laptop or a tablet but not both.
(i) Copy and complete the following tree diagram. (Do not write on this page.)
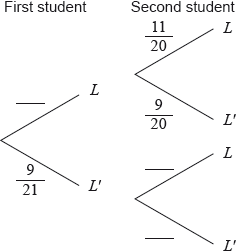
(ii) Write down the probability that the second student owns a laptop given that the first owns a laptop.
Answer/Explanation
Markscheme
(i) \(p = 3\) A1 N1
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)\((12 + 10 + 3) – 21,{\text{ }}22 – 18\)
\(q = 4\) A1 N2
(iii) \(r = 8,{\text{ }}s = 6\) A1A1 N2
(i) \(\frac{{12}}{{21}}{\text{ }}\left( { = \frac{4}{7}} \right)\) A2 N2
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)\(8 + 6,{\text{ }}r + s\)
\(\frac{{14}}{{21}}{\text{ }}\left( { = \frac{2}{3}} \right)\) A1 N2
(i)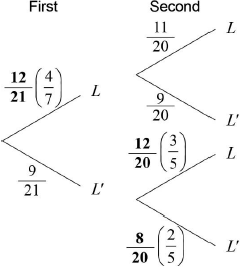 
A1A1A1 N3
(ii) \(\frac{{11}}{{20}}\) A1 N1
[4 marks]
Question
In a group of 20 girls, 13 take history and 8 take economics. Three girls take both history and economics, as shown in the following Venn diagram. The values \(p\) and \(q\) represent numbers of girls.
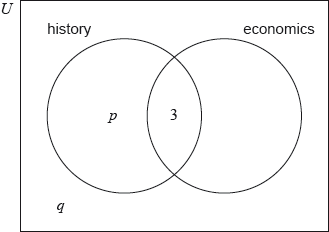
Find the value of \(p\);
Find the value of \(q\).
A girl is selected at random. Find the probability that she takes economics but not history.
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(p + 3 = 13,{\text{ }}13 – 3\)
\(p = 10\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(p + 3 + 5 + q = 20,{\text{ }}10 – 10 – 8\)
\(q = 2\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(20 – p – q – 3,{\text{ }}1 – \frac{{15}}{{20}},{\text{ }}n(E \cap H’) = 5\)
\(\frac{5}{{20}}\,\,\,\left( {\frac{1}{4}} \right)\) A1 N2
[2 marks]
Question
A bag contains 5 green balls and 3 white balls. Two balls are selected at random without replacement.
Complete the following tree diagram.
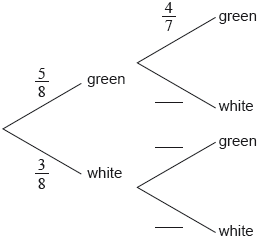
Find the probability that exactly one of the selected balls is green.
Answer/Explanation
Markscheme
correct probabilities
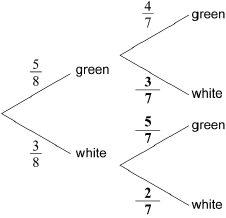A1A1A1 N3
Note: Award A1 for each correct bold answer.
[3 marks]
multiplying along branches (M1)
eg\(\,\,\,\,\,\)\(\frac{5}{8} \times \frac{3}{7},{\text{ }}\frac{3}{8} \times \frac{5}{7},{\text{ }}\frac{{15}}{{56}}\)
adding probabilities of correct mutually exclusive paths (A1)
eg\(\,\,\,\,\,\)\(\frac{5}{8} \times \frac{3}{7} + \frac{3}{8} \times \frac{5}{7},{\text{ }}\frac{{15}}{{56}} + \frac{{15}}{{56}}\)
\(\frac{{30}}{{56}}{\text{ }}\left( { = \frac{{15}}{{28}}} \right)\) A1 N2
[3 marks]
Question
Pablo drives to work. The probability that he leaves home before 07:00 is \(\frac{3}{4}\).
If he leaves home before 07:00 the probability he will be late for work is \(\frac{1}{8}\).
If he leaves home at 07:00 or later the probability he will be late for work is \(\frac{5}{8}\).
Copy and complete the following tree diagram.
Find the probability that Pablo leaves home before 07:00 and is late for work.
Find the probability that Pablo is late for work.
Given that Pablo is late for work, find the probability that he left home before 07:00.
Two days next week Pablo will drive to work. Find the probability that he will be late at least once.
Answer/Explanation
Markscheme
A1A1A1 N3
Note: Award A1 for each bold fraction.
[3 marks]
multiplying along correct branches (A1)
eg \(\frac{3}{4} \times \frac{1}{8}\)
P(leaves before 07:00 ∩ late) = \(\frac{3}{32}\) A1 N2
[2 marks]
multiplying along other “late” branch (M1)
eg \(\frac{1}{4} \times \frac{5}{8}\)
adding probabilities of two mutually exclusive late paths (A1)
eg \(\left( {\frac{3}{4} \times \frac{1}{8}} \right) + \left( {\frac{1}{4} \times \frac{5}{8}} \right),\,\,\frac{3}{{32}} + \frac{5}{{32}}\)
\({\text{P}}\left( L \right) = \frac{8}{{32}}\,\,\left( { = \frac{1}{4}} \right)\) A1 N2
[3 marks]
recognizing conditional probability (seen anywhere) (M1)
eg \({\text{P}}\left( {A|B} \right),\,\,{\text{P}}\left( {{\text{before 7}}|{\text{late}}} \right)\)
correct substitution of their values into formula (A1)
eg \(\frac{{\frac{3}{{32}}}}{{\frac{1}{4}}}\)
\({\text{P}}\left( {{\text{left before 07:00}}|{\text{late}}} \right) = \frac{3}{8}\) A1 N2
[3 marks]
valid approach (M1)
eg 1 − P(not late twice), P(late once) + P(late twice)
correct working (A1)
eg \(1 – \left( {\frac{3}{4} \times \frac{3}{4}} \right),\,\,2 \times \frac{1}{4} \times \frac{3}{4} + \frac{1}{4} \times \frac{1}{4}\)
\(\frac{7}{{16}}\) A1 N2
[3 marks]