Question
There are 20 students in a classroom. Each student plays only one sport. The table below gives their sport and gender.
One student is selected at random.
(i) Calculate the probability that the student is a male or is a tennis player.
(ii) Given that the student selected is female, calculate the probability that the student does not play football.
Two students are selected at random. Calculate the probability that neither student plays football.
Answer/Explanation
Markscheme
(i) correct calculation (A1)
e.g. \(\frac{9}{{20}} + \frac{5}{{20}} – \frac{2}{{20}}\) , \(\frac{{4 + 2 + 3 + 3}}{{20}}\)
\({\text{P(male or tennis)}} = \frac{{12}}{{20}}\) A1 N2
(ii) correct calculation (A1)
e.g. \(\frac{6}{{20}} \div \frac{{11}}{{20}}\) , \(\frac{{3 + 3}}{{11}}\)
\({\text{P(not football|female)}} = \frac{6}{{11}}\) A1 N2
[4 marks]
\({\text{P(first not football)}} = \frac{{11}}{{20}}\) , \({\text{P(second not football)}} = \frac{{10}}{{19}}\) A1
\({\text{P(neither football)}} = \frac{{11}}{{20}} \times \frac{{10}}{{19}}\) A1
\({\text{P(neither football)}} = \frac{{110}}{{380}}\) A1 N1
[3 marks]
Question
The letters of the word PROBABILITY are written on 11 cards as shown below.
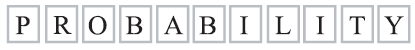
Two cards are drawn at random without replacement.
Let A be the event the first card drawn is the letter A.
Let B be the event the second card drawn is the letter B.
Find \({\rm{P}}(A)\) .
Find \({\rm{P}}(B|A)\) .
Find \({\rm{P}}(A \cap B)\) .
Answer/Explanation
Markscheme
\({\rm{P}}(A) = \frac{1}{{11}}\) A1 N1
[1 mark]
\({\rm{P}}(B|A) = \frac{2}{{10}}\) A2 N2
[2 marks]
recognising that \({\rm{P}}(A \cap B) = {\rm{P}}(A) \times {\rm{P}}(B|A)\) (M1)
correct values (A1)
e.g. \({\rm{P}}(A \cap B) = \frac{1}{{11}} \times \frac{2}{{10}}\)
\({\rm{P}}(A \cap B) = \frac{2}{{110}}\) A1 N3
[3 marks]
Question
A box contains six red marbles and two blue marbles. Anna selects a marble from the box. She replaces the marble and then selects a second marble.
Write down the probability that the first marble Anna selects is red.
Find the probability that Anna selects two red marbles.
Find the probability that one marble is red and one marble is blue.
Answer/Explanation
Markscheme
Note: In this question, method marks may be awarded for selecting without replacement, as noted in the examples.
\({\rm{P}}(R) = \frac{6}{8}\left( { = \frac{3}{4}} \right)\) A1 N1
[1 mark]
attempt to find \({\rm{P(Red)}} \times {\rm{P(Red)}}\) (M1)
e.g. \({\rm{P(}}R{\rm{)}} \times {\rm{P(}}R{\rm{)}}\) , \(\frac{3}{4} \times \frac{3}{4}\) , \(\frac{6}{8} \times \frac{5}{7}\)
\({\rm{P}}(2R) = \frac{{36}}{{64}}\left( { = \frac{9}{{16}}} \right)\) A1 N2
[2 marks]
METHOD 1
attempt to find \({\rm{P(Red)}} \times {\rm{P(Blue)}}\) (M1)
e.g. \({\rm{P(}}R{\rm{)}} \times {\rm{P(}}B{\rm{)}}\) , \(\frac{6}{8} \times \frac{2}{8}\) , \(\frac{6}{8} \times \frac{2}{7}\)
recognizing two ways to get one red, one blue (M1)
e.g. \({\rm{P}}(RB) + {\rm{P}}(BR)\) , \(2\left( {\frac{{12}}{{64}}} \right)\) , \(\frac{6}{8} \times \frac{2}{7} + \frac{2}{8} \times \frac{6}{7}\)
\({\rm{P}}(1R,1B) = \frac{{24}}{{64}}\left( { = \frac{3}{8}} \right)\) A1 N2
[3 marks]
METHOD 2
recognizing that \({\rm{P}}(1R,1B)\) is \(1 – {\rm{P}}(2B) – {\rm{P}}(2R)\) (M1)
attempt to find \({\rm{P}}(2R)\) and \({\rm{P}}(2B)\) (M1)
e.g. \({\rm{P}}(2R) = \frac{3}{4} \times \frac{3}{4}\) , \(\frac{6}{8} \times \frac{5}{7}\) ; \({\rm{P}}(2B) = \frac{1}{4} \times \frac{1}{4}\) , \(\frac{2}{8} \times \frac{1}{7}\)
\({\rm{P}}(1R,1B) = \frac{{24}}{{64}}\left( { = \frac{3}{8}} \right)\) A1 N2
[3 marks]
Question
Jar A contains three red marbles and five green marbles. Two marbles are drawn from the jar, one after the other, without replacement.
Jar B contains six red marbles and two green marbles. A fair six-sided die is tossed. If the score is \(1\) or \(2\), a marble is drawn from jar A. Otherwise, a marble is drawn from jar B.
Find the probability that
(i) none of the marbles are green;
(ii) exactly one marble is green.
Find the expected number of green marbles drawn from the jar.
(i) Write down the probability that the marble is drawn from jar B.
(ii) Given that the marble was drawn from jar B, write down the probability that it is red.
Given that the marble is red, find the probability that it was drawn from jar A.
Answer/Explanation
Markscheme
(i) attempt to find \({\rm{P(red)}} \times {\rm{P(red)}}\) (M1)
eg \(\frac{3}{8} \times \frac{2}{7}\) , \(\frac{3}{8} \times \frac{3}{8}\) , \(\frac{3}{8} \times \frac{2}{8}\)
\({\text{P(none green)}} = \frac{6}{{56}}\) \(\left( { = \frac{3}{{28}}} \right)\) A1 N2
(ii) attempt to find \({\rm{P(red)}} \times {\rm{P(green)}}\) (M1)
eg \(\frac{5}{8} \times \frac{3}{7}\) , \(\frac{3}{8} \times \frac{5}{8}\) , \(\frac{{15}}{{56}}\)
recognizing two ways to get one red, one green (M1)
eg \(2{\rm{P}}(R) \times {\rm{P}}(G)\) , \(\frac{5}{8} \times \frac{3}{7} + \frac{3}{8} \times \frac{5}{7}\) , \(\frac{3}{8} \times \frac{5}{8} \times 2\)
\({\text{P(exactly one green)}} = \frac{{30}}{{56}}\) \(\left( { = \frac{{15}}{{28}}} \right)\) A1 N2
[5 marks]
\({\text{P(both green)}} = \frac{{20}}{{56}}\) (seen anywhere) (A1)
correct substitution into formula for \({\rm{E}}(X)\) A1
eg \(0 \times \frac{6}{{56}} + 1 \times \frac{{30}}{{56}} + 2 \times \frac{{20}}{{56}}\) , \(\frac{{30}}{{64}} + \frac{{50}}{{64}}\)
expected number of green marbles is \(\frac{{70}}{{56}}\) \(\left( { = \frac{5}{4}} \right)\) A1 N2
[3 marks]
(i) \({\text{P(jar B)}} = \frac{4}{6}\) \(\left( { = \frac{2}{3}} \right)\) A1 N1
(ii) \({\text{P(red| jar B)}} = \frac{6}{8}\) \(\left( { = \frac{3}{4}} \right)\) A1 N1
[2 marks]
recognizing conditional probability (M1)
eg \({\rm{P}}(A|R)\) , \(\frac{{{\text{P(jar A and red)}}}}{{{\rm{P(red)}}}}\) , tree diagram
attempt to multiply along either branch (may be seen on diagram) (M1)
eg \({\text{P(jar A and red)}} = \frac{1}{3} \times \frac{3}{8}\) \(\left( { = \frac{1}{8}} \right)\)
attempt to multiply along other branch (M1)
eg \({\text{P(jar B and red)}} = \frac{2}{3} \times \frac{6}{8}\) \(\left( { = \frac{1}{2}} \right)\)
adding the probabilities of two mutually exclusive paths (A1)
eg \({\rm{P(red)}} = \frac{1}{3} \times \frac{3}{8} + \frac{2}{3} \times \frac{6}{8}\)
correct substitution
eg \({\text{P(jar A|red)}} = \frac{{\frac{1}{3} \times \frac{3}{8}}}{{\frac{1}{3} \times \frac{3}{8} + \frac{2}{3} \times \frac{6}{8}}}\) , \(\frac{{\frac{1}{8}}}{{\frac{5}{8}}}\) A1
\({\text{P(jar A|red)}} = \frac{1}{5}\) A1 N3
[6 marks]
Question
In a class of 21 students, 12 own a laptop, 10 own a tablet, and 3 own neither.
The following Venn diagram shows the events “own a laptop” and “own a tablet”.
The values \(p\), \(q\), \(r\) and \(s\) represent numbers of students.
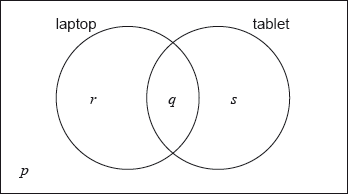
A student is selected at random from the class.
Two students are randomly selected from the class. Let \(L\) be the event a “student owns a laptop”.
(i) Write down the value of \(p\).
(ii) Find the value of \(q\).
(iii) Write down the value of \(r\) and of \(s\).
(i) Write down the probability that this student owns a laptop.
(ii) Find the probability that this student owns a laptop or a tablet but not both.
(i) Copy and complete the following tree diagram. (Do not write on this page.)
(ii) Write down the probability that the second student owns a laptop given that the first owns a laptop.
Answer/Explanation
Markscheme
(i) \(p = 3\) A1 N1
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)\((12 + 10 + 3) – 21,{\text{ }}22 – 18\)
\(q = 4\) A1 N2
(iii) \(r = 8,{\text{ }}s = 6\) A1A1 N2
(i) \(\frac{{12}}{{21}}{\text{ }}\left( { = \frac{4}{7}} \right)\) A2 N2
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)\(8 + 6,{\text{ }}r + s\)
\(\frac{{14}}{{21}}{\text{ }}\left( { = \frac{2}{3}} \right)\) A1 N2
(i)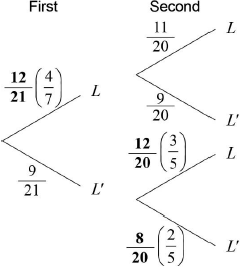 
A1A1A1 N3
(ii) \(\frac{{11}}{{20}}\) A1 N1
[4 marks]
Question
In a group of 20 girls, 13 take history and 8 take economics. Three girls take both history and economics, as shown in the following Venn diagram. The values \(p\) and \(q\) represent numbers of girls.
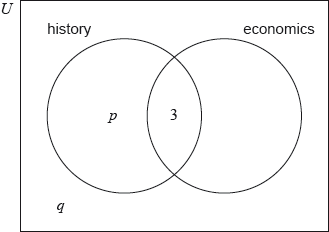
Find the value of \(p\);
Find the value of \(q\).
A girl is selected at random. Find the probability that she takes economics but not history.
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(p + 3 = 13,{\text{ }}13 – 3\)
\(p = 10\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(p + 3 + 5 + q = 20,{\text{ }}10 – 10 – 8\)
\(q = 2\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(20 – p – q – 3,{\text{ }}1 – \frac{{15}}{{20}},{\text{ }}n(E \cap H’) = 5\)
\(\frac{5}{{20}}\,\,\,\left( {\frac{1}{4}} \right)\) A1 N2
[2 marks]
Question
Pablo drives to work. The probability that he leaves home before 07:00 is \(\frac{3}{4}\).
If he leaves home before 07:00 the probability he will be late for work is \(\frac{1}{8}\).
If he leaves home at 07:00 or later the probability he will be late for work is \(\frac{5}{8}\).
Copy and complete the following tree diagram.
Find the probability that Pablo leaves home before 07:00 and is late for work.
Find the probability that Pablo is late for work.
Given that Pablo is late for work, find the probability that he left home before 07:00.
Two days next week Pablo will drive to work. Find the probability that he will be late at least once.
Answer/Explanation
Markscheme
A1A1A1 N3
Note: Award A1 for each bold fraction.
[3 marks]
multiplying along correct branches (A1)
eg \(\frac{3}{4} \times \frac{1}{8}\)
P(leaves before 07:00 ∩ late) = \(\frac{3}{32}\) A1 N2
[2 marks]
multiplying along other “late” branch (M1)
eg \(\frac{1}{4} \times \frac{5}{8}\)
adding probabilities of two mutually exclusive late paths (A1)
eg \(\left( {\frac{3}{4} \times \frac{1}{8}} \right) + \left( {\frac{1}{4} \times \frac{5}{8}} \right),\,\,\frac{3}{{32}} + \frac{5}{{32}}\)
\({\text{P}}\left( L \right) = \frac{8}{{32}}\,\,\left( { = \frac{1}{4}} \right)\) A1 N2
[3 marks]
recognizing conditional probability (seen anywhere) (M1)
eg \({\text{P}}\left( {A|B} \right),\,\,{\text{P}}\left( {{\text{before 7}}|{\text{late}}} \right)\)
correct substitution of their values into formula (A1)
eg \(\frac{{\frac{3}{{32}}}}{{\frac{1}{4}}}\)
\({\text{P}}\left( {{\text{left before 07:00}}|{\text{late}}} \right) = \frac{3}{8}\) A1 N2
[3 marks]
valid approach (M1)
eg 1 − P(not late twice), P(late once) + P(late twice)
correct working (A1)
eg \(1 – \left( {\frac{3}{4} \times \frac{3}{4}} \right),\,\,2 \times \frac{1}{4} \times \frac{3}{4} + \frac{1}{4} \times \frac{1}{4}\)
\(\frac{7}{{16}}\) A1 N2
[3 marks]