Question
The following table shows the probability distribution of a discrete random variable X.

Find the value of k.
Find the expected value of X.
Answer/Explanation
Markscheme
evidence of using \(\sum {{p_i} = 1} \) (M1)
correct substitution A1
e.g. \(10{k^2} + 3k + 0.6 = 1\) , \(10{k^2} + 3k – 0.4 = 0\)
\(k = 0.1\) A2 N2
[4 marks]
evidence of using \({\rm{E}}(X) = \sum {{p_i}{x_i}} \) (M1)
correct substitution (A1)
e.g. \( – 1 \times 0.2 + 2 \times 0.4 + 3 \times 0.3\)
\({\rm{E}}(X) = 1.5\) A1 N2
[3 marks]
Question
A test has five questions. To pass the test, at least three of the questions must be answered correctly.
The probability that Mark answers a question correctly is \(\frac{1}{5}\) . Let X be the number of questions that Mark answers correctly.
Bill also takes the test. Let Y be the number of questions that Bill answers correctly.
The following table is the probability distribution for Y .
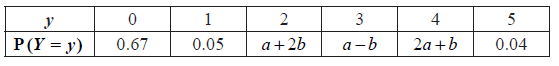
(i) Find E(X ) .
(ii) Find the probability that Mark passes the test.
(i) Show that \(4a + 2b = 0.24\) .
(ii) Given that \({\rm{E}}(Y) = 1\) , find a and b .
Find which student is more likely to pass the test.
Answer/Explanation
Markscheme
(i) valid approach (M1)
e.g. \(np\) , \(5 \times \frac{1}{5}\)
\({\rm{E}}(X) = 1\) A1 N2
(ii) evidence of appropriate approach involving binomial (M1)
e.g. \(X \sim B\left( {5,\frac{1}{5}} \right)\)
recognizing that Mark needs to answer 3 or more questions correctly (A1)
e.g. \({\rm{P}}(X \ge 3)\)
valid approach M1
e.g. \(1 – {\rm{P}}(X \le 2)\) , \({\rm{P}}(X = 3) + {\rm{P}}(X = 4) + {\rm{P}}(X = 5)\)
\({\text{P(pass)}} = 0.0579\) A1 N3
[6 marks]
(i) evidence of summing probabilities to 1 (M1)
e.g. \(0.67 + 0.05 + (a + 2b) + \ldots + 0.04 = 1\)
some simplification that clearly leads to required answer
e.g. \(0.76 + 4a + 2b = 1\) A1
\(4a + 2b = 0.24\) AG N0
(ii) correct substitution into the formula for expected value (A1)
e.g. \(0(0.67) + 1(0.05) + \ldots + 5(0.04)\)
some simplification (A1)
e.g. \(0.05 + 2a + 4b + \ldots + 5(0.04) = 1\)
correct equation A1
e.g. \(13a + 5b = 0.75\)
evidence of solving (M1)
\(a = 0.05\) , \(b = 0.02\) A1A1 N4
[8 marks]
attempt to find probability Bill passes (M1)
e.g. \({\rm{P}}(Y \ge 3)\)
correct value 0.19 A1
Bill (is more likely to pass) A1 N0
[3 marks]
Question
The following table shows the probability distribution of a discrete random variable \(X\).
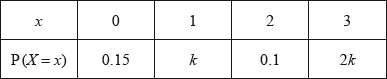
Find the value of \(k\).
Find \({\text{E}}(X)\).
Answer/Explanation
Markscheme
evidence of using \(\sum {{p_i}} = 1\) (M1)
correct substitution A1
eg\(\;\;\;0.15 + k + 0.1 + 2k = 1,{\text{ }}3k + 0.25 = 1\)
\(k = 0.25\) A1 N2
[3 marks]
correct substitution (A1)
eg\(\;\;\;0 \times 0.15 + 1 \times 0.25 + 2 \times 0.1 + 3 \times 0.5\)
\({\text{E}}(X) = 1.95\) A1 N2
[2 marks]
Total [5 marks]
Question
A factory has two machines, A and B. The number of breakdowns of each machine is independent from day to day.
Let \(A\) be the number of breakdowns of Machine A on any given day. The probability distribution for \(A\) can be modelled by the following table.

Let \(B\) be the number of breakdowns of Machine B on any given day. The probability distribution for \(B\) can be modelled by the following table.

On Tuesday, the factory uses both Machine A and Machine B. The variables \(A\) and \(B\) are independent.
Find \(k\).
(i) A day is chosen at random. Write down the probability that Machine A has no breakdowns.
(ii) Five days are chosen at random. Find the probability that Machine A has no breakdowns on exactly four of these days.
Find \({\text{E}}(B)\).
(i) Find the probability that there are exactly two breakdowns on Tuesday.
(ii) Given that there are exactly two breakdowns on Tuesday, find the probability that both breakdowns are of Machine A.
Answer/Explanation
Markscheme
evidence of summing to 1 (M1)
eg\(\,\,\,\,\,\)\(0.55 + 0.3 + 0.1 + k = 1\)
\(k = 0.05{\text{ (exact)}}\) A1 N2
[2 marks]
(i) 0.55 A1 N1
(ii) recognizing binomial probability (M1)
eg\(\,\,\,\,\,\)\(X:{\text{ }}B(n,{\text{ }}p),{\text{ }}\left( {\begin{array}{*{20}{c}} 5 \\ 4 \end{array}} \right),{\text{ }}{(0.55)^4}(1 – 0.55),{\text{ }}\left( {\begin{array}{*{20}{c}} n \\ r \end{array}} \right){p^r}{q^{n – r}}\)
\(P(X = 4) = 0.205889\)
\(P(X = 4) = 0.206\) A1 N2
[3 marks]
correct substitution into formula for \({\text{E}}(X)\) (A1)
eg\(\,\,\,\,\,\)\(0.2 + (2 \times 0.08) + (3 \times 0.02)\)
\({\text{E}}(B) = 0.42{\text{ (exact)}}\) A1 N2
[2 marks]
(i) valid attempt to find one possible way of having 2 breakdowns (M1)
eg\(\,\,\,\,\,\)\(2A,{\text{ }}2B,{\text{ }}1A\) and \(1B\), tree diagram
one correct calculation for 1 way (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\(0.1 \times 0.7,{\text{ }}0.55 \times 0.08,{\text{ }}0.3 \times 0.2\)
recognizing there are 3 ways of having 2 breakdowns (M1)
eg\(\,\,\,\,\,\)A twice or B twice or one breakdown each
correct working (A1)
eg\(\,\,\,\,\,\)\((0.1 \times 0.7) + (0.55 \times 0.08) + (0.3 \times 0.2)\)
\({\text{P(2 breakdowns)}} = 0.174{\text{ (exact)}}\) A1 N3
(ii) recognizing conditional probability (M1)
eg\(\,\,\,\,\,\)\({\text{P}}(A|B),{\text{ P}}(2A|{\text{2breakdowns}})\)
correct working (A1)
eg\(\,\,\,\,\,\)\(\frac{{0.1 \times 0.7}}{{0.174}}\)
\({\text{P}}(A = 2|{\text{two breakdowns}}) = 0.402298\)
\({\text{P}}(A = 2|{\text{two breakdowns}}) = 0.402\) A1 N2
[8 marks]
Question
In a large university the probability that a student is left handed is 0.08. A sample of 150 students is randomly selected from the university. Let \(k\) be the expected number of left-handed students in this sample.
Find \(k\).
Hence, find the probability that exactly \(k\) students are left handed;
Hence, find the probability that fewer than \(k\) students are left handed.
Answer/Explanation
Markscheme
evidence of binomial distribution (may be seen in part (b)) (M1)
eg\(\,\,\,\,\,\)\(np,{\text{ }}150 \times 0.08\)
\(k = 12\) A1 N2
[2 marks]
\({\text{P}}\left( {X = 12} \right) = \left( {\begin{array}{*{20}{c}}
{150} \\
{12}
\end{array}} \right){\left( {0.08} \right)^{12}}{\left( {0.92} \right)^{138}}\) (A1)
0.119231
probability \( = 0.119\) A1 N2
[2 marks]
recognition that \(X \leqslant 11\) (M1)
0.456800
\({\text{P}}(X < 12) = 0.457\) A1 N2
[2 marks]
Question
A biased four-sided die is rolled. The following table gives the probability of each score.
Find the value of k.
Calculate the expected value of the score.
The die is rolled 80 times. On how many rolls would you expect to obtain a three?
Answer/Explanation
Markscheme
evidence of summing to 1 (M1)
eg 0.28 + k + 1.5 + 0.3 = 1, 0.73 + k = 1
k = 0.27 A1 N2
[2 marks]
correct substitution into formula for E (X) (A1)
eg 1 × 0.28 + 2 × k + 3 × 0.15 + 4 × 0.3
E (X) = 2.47 (exact) A1 N2
[2 marks]
valid approach (M1)
eg np, 80 × 0.15
12 A1 N2
[2 marks]

