Question
A factory makes switches. The probability that a switch is defective is 0.04. The factory tests a random sample of 100 switches.
Find the mean number of defective switches in the sample.
Find the probability that there are exactly six defective switches in the sample.
Find the probability that there is at least one defective switch in the sample.
Answer/Explanation
Markscheme
evidence of binomial distribution (may be seen in parts (b) or (c)) (M1)
e.g. np, \(100 \times 0.04\)
\({\text{mean}} = 4\) A1 N2
[2 marks]
\({\rm{P}}(X = 6) = \left( {\begin{array}{*{20}{c}}
{100}\\
6
\end{array}} \right){(0.04)^6}{(0.96)^{94}}\) (A1)
\( = 0.105\) A1 N2
[2 marks]
for evidence of appropriate approach (M1)
e.g. complement, \(1 – {\rm{P}}(X = 0)\)
\({\rm{P}}(X = 0) = {(0.96)^{100}} = 0.01687 \ldots \) (A1)
\({\rm{P}}(X \ge 1) = 0.983\) A1 N2
[3 marks]
Question
Paula goes to work three days a week. On any day, the probability that she goes on a red bus is \(\frac{1}{4}\) .
Write down the expected number of times that Paula goes to work on a red bus in one week.
In one week, find the probability that she goes to work on a red bus on exactly two days.
In one week, find the probability that she goes to work on a red bus on at least one day.
Answer/Explanation
Markscheme
evidence of binomial distribution (seen anywhere) (M1)
e.g. \(X \sim {\text{B}}\left( {3{\text{, }}\frac{1}{4}} \right)\)
\({\rm{mean}} = \frac{3}{4}\) (\(= 0.75\)) A1 N2
[2 marks]
\({\rm{P}}(X = 2) = \left( {\begin{array}{*{20}{c}}
3\\
2
\end{array}} \right){\left( {\frac{1}{4}} \right)^2}\left( {\frac{3}{4}} \right)\) (A1)
\({\rm{P}}(X = 2) = 0.141\) \(\left( { = \frac{9}{{64}}} \right)\) A1 N2
[2 marks]
evidence of appropriate approach M1
e.g. complement, \(1 – {\rm{P}}(X = 0)\) , adding probabilities
\({\rm{P}}(X = 0) = {(0.75)^3}\) \(\left( { = 0.422,\frac{{27}}{{64}}} \right)\) (A1)
\({\rm{P}}(X \ge 1) = 0.578\) \(\left( { = \frac{{37}}{{64}}} \right)\) A1 N2
[3 marks]
Question
The probability of obtaining heads on a biased coin is 0.18. The coin is tossed seven times.
Find the probability of obtaining exactly two heads.
Find the probability of obtaining at least two heads.
Answer/Explanation
Markscheme
evidence of using binomial probability (M1)
e.g. \({\rm{P}}(X = 2) = \left( {\begin{array}{*{20}{c}}
7\\
2
\end{array}} \right){(0.18)^2}{(0.82)^5}\)
\({\rm{P}}(X = 2) = 0.252\) A1 N2
[2 marks]
METHOD 1
evidence of using the complement M1
e.g. \(1 – ({\rm{P}}(X \le 1))\)
\({\text{P}}(X \le 1) = 0.632\) (A1)
\({\text{P}}(X \ge 2) = 0.368\) A1 N2
METHOD 2
evidence of attempting to sum probabilities M1
e.g. \({\text{P(2 heads) + P(3 heads)}} + \ldots + {\text{P(7 heads)}}\) , \(0.252 + 0.0923 + \ldots \)
correct values for each probability (A1)
e.g. \(0.252 + 0.0923 + 0.0203 + 0.00267 + 0.0002 + 0.0000061\)
\({\text{P(}}X \ge {\rm{2) = 0}}{\rm{.368}}\) A1 N2
[3 marks]
Question
A van can take either Route A or Route B for a particular journey.
If Route A is taken, the journey time may be assumed to be normally distributed with mean 46 minutes and a standard deviation 10 minutes.
If Route B is taken, the journey time may be assumed to be normally distributed with mean \(\mu \) minutes and standard deviation 12 minutes.
For Route A, find the probability that the journey takes more than \(60\) minutes.
For Route B, the probability that the journey takes less than \(60\) minutes is \(0.85\).
Find the value of \(\mu \) .
The van sets out at 06:00 and needs to arrive before 07:00.
(i) Which route should it take?
(ii) Justify your answer.
On five consecutive days the van sets out at 06:00 and takes Route B. Find the probability that
(i) it arrives before 07:00 on all five days;
(ii) it arrives before 07:00 on at least three days.
Answer/Explanation
Markscheme
\(A \sim N(46{\text{, }}{10^2})\) \(B \sim N(\mu {\text{, }}{12^2})\)
\({\rm{P}}(A > 60) = 0.0808\) A2 N2
[2 marks]
correct approach (A1)
e.g. \({\rm{P}}\left( {Z < \frac{{60 – \mu }}{{12}}} \right) = 0.85\) , sketch
\(\frac{{60 – \mu }}{{12}} = 1.036 \ldots \) (A1)
\(\mu = 47.6\) A1 N2
[3 marks]
(i) route A A1 N1
(ii) METHOD 1
\({\rm{P}}(A < 60) = 1 – 0.0808 = 0.9192\) A1
valid reason R1
e.g. probability of A getting there on time is greater than probability of B
\(0.9192 > 0.85\) N2
METHOD 2
\({\rm{P}}(B > 60) = 1 – 0.85 = 0.15\) A1
valid reason R1
e.g. probability of A getting there late is less than probability of B
\(0.0808 < 0.15\) N2
[3 marks]
(i) let X be the number of days when the van arrives before 07:00
\({\rm{P}}(X = 5) = {(0.85)^5}\) (A1)
\( = 0.444\) A1 N2
(ii) METHOD 1
evidence of adding correct probabilities (M1)
e.g. \({\rm{P}}(X \ge 3) = {\rm{P}}(X = 3) + {\rm{P}}(X = 4) + {\rm{P}}(X = 5)\)
correct values \(0.1382 + 0.3915 + 0.4437\) (A1)
\({\rm{P}}(X \ge 3) = 0.973\) A1 N3
METHOD 2
evidence of using the complement (M1)
e.g. \({\rm{P}}(X \ge 3) = 1 – {\rm{P}}(X \le 2)\) , \(1 – p\)
correct values \(1 – 0.02661\) (A1)
\({\rm{P}}(X \ge 3) = 0.973\) A1 N3
[5 marks]
Examiners report
A significant number of students clearly understood what was asked in part (a) and used the GDC to find the result.
In part (b), many candidates set the standardized formula equal to the probability (\(0.85\)), instead of using the corresponding z-score. Other candidates used the solver on their GDC with the inverse norm function.
A common incorrect approach in part (c) was to attempt to use the means and standard deviations for justification, although many candidates successfully considered probabilities.
A pleasing number of candidates recognized the binomial probability and made progress on part (d).
Question
A multiple choice test consists of ten questions. Each question has five answers. Only one of the answers is correct. For each question, Jose randomly chooses one of the five answers.
Find the expected number of questions Jose answers correctly.
Find the probability that Jose answers exactly three questions correctly.
Find the probability that Jose answers more than three questions correctly.
Answer/Explanation
Markscheme
\({\rm{E}}(X) = 2\) A1 N1
[1 mark]
evidence of appropriate approach involving binomial (M1)
e.g. \(\left( {\begin{array}{*{20}{c}}
{10}\\
3
\end{array}} \right){(0.2)^3}\) , \({(0.2)^3}{(0.8)^7}\) , \(X \sim {\rm{B}}(10,0.2)\)
\({\rm{P}}(X = 3) = 0.201\) A1 N2
[2 marks]
METHOD 1
\({\rm{P}}(X \le 3) = 0.10737 + 0.26844 + 0.30199 + 0.20133\) \(( = 0.87912 \ldots )\) (A1)
evidence of using the complement (seen anywhere) (M1)
e.g. \(1 – \) any probability , \({\rm{P}}(X > 3) = 1 – {\rm{P}}(X \le 3)\)
\({\rm{P}}(X > 3) = 0.121\) A1 N2
METHOD 2
recognizing that \({\rm{P}}(X > 3) = {\rm{P}}(X \ge 4)\) (M1)
e.g. summing probabilities from \(X = 4\) to \(X = 10\)
correct expression or values (A1)
e.g. \(\sum\limits_{r = 4}^{10} {\left( {\begin{array}{*{20}{c}}
{10}\\
r
\end{array}} \right)} {(0.2)^{10 – r}}{(0.8)^r}\)
\(0.08808 + 0.02642 + 0.005505 + 0.000786 + 0.0000737 + 0.000004 + 0.0000001\)
\({\rm{P}}(X > 3) = 0.121\) A1 N2
[3 marks]
Question
Evan likes to play two games of chance, A and B.
For game A, the probability that Evan wins is 0.9. He plays game A seven times.
For game B, the probability that Evan wins is p . He plays game B seven times.
Find the probability that he wins exactly four games.
Write down an expression, in terms of p , for the probability that he wins exactly four games.
Hence, find the values of p such that the probability that he wins exactly four games is 0.15.
Answer/Explanation
Markscheme
evidence of recognizing binomial probability (may be seen in (b) or (c)) (M1)
e.g. probability \( = \left( {\begin{array}{*{20}{c}}
7\\
4
\end{array}} \right){(0.9)^4}{(0.1)^3}\) , \(X \sim {\rm{B}}(7,0.9)\) , complementary probabilities
probability \(= 0.0230\) A1 N2
[2 marks]
correct expression A1A1 N2
e.g. \(\left( {\begin{array}{*{20}{c}}
7\\
4
\end{array}} \right){p^4}{(1 – p)^3}\) , \(35{p^4}{(1 – p)^3}\)
Note: Award A1 for binomial coefficient (accept \(\left( {\begin{array}{*{20}{c}}
7\\
3
\end{array}} \right)\) ) , A1 for \({p^4}{(1 – p)^3}\) .
[2 marks]
evidence of attempting to solve their equation (M1)
e.g. \(\left( {\begin{array}{*{20}{c}}
7\\
4
\end{array}} \right){p^4}{(1 – p)^3} = 0.15\) , sketch
\(p = 0.356\), \(0.770\) A1A1 N3
[3 marks]
Question
Jan plays a game where she tosses two fair six-sided dice. She wins a prize if the sum of her scores is 5.
Jan tosses the two dice once. Find the probability that she wins a prize.
Jan tosses the two dice 8 times. Find the probability that she wins 3 prizes.
Answer/Explanation
Markscheme
36 outcomes (seen anywhere, even in denominator) (A1)
valid approach of listing ways to get sum of 5, showing at least two pairs (M1)
e.g. (1, 4)(2, 3), (1, 4)(4, 1), (1, 4)(4, 1), (2, 3)(3, 2) , lattice diagram
\({\rm{P(prize)}} = \frac{4}{{36}}\) \(\left( { = \frac{1}{9}} \right)\) A1 N3
[3 marks]
recognizing binomial probability (M1)
e.g. \({\rm{B}}\left( {8,\frac{1}{9}} \right)\) , binomial pdf, \(\left( {\begin{array}{*{20}{c}}
8\\
3
\end{array}} \right){\left( {\frac{1}{9}} \right)^3}{\left( {\frac{8}{9}} \right)^5}\)
\({\text{P(3 prizes)}} = 0.0426\) A1 N2
[2 marks]
Question
A test has five questions. To pass the test, at least three of the questions must be answered correctly.
The probability that Mark answers a question correctly is \(\frac{1}{5}\) . Let X be the number of questions that Mark answers correctly.
Bill also takes the test. Let Y be the number of questions that Bill answers correctly.
The following table is the probability distribution for Y .
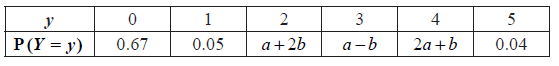
(i) Find E(X ) .
(ii) Find the probability that Mark passes the test.
(i) Show that \(4a + 2b = 0.24\) .
(ii) Given that \({\rm{E}}(Y) = 1\) , find a and b .
Find which student is more likely to pass the test.
Answer/Explanation
Markscheme
(i) valid approach (M1)
e.g. \(np\) , \(5 \times \frac{1}{5}\)
\({\rm{E}}(X) = 1\) A1 N2
(ii) evidence of appropriate approach involving binomial (M1)
e.g. \(X \sim B\left( {5,\frac{1}{5}} \right)\)
recognizing that Mark needs to answer 3 or more questions correctly (A1)
e.g. \({\rm{P}}(X \ge 3)\)
valid approach M1
e.g. \(1 – {\rm{P}}(X \le 2)\) , \({\rm{P}}(X = 3) + {\rm{P}}(X = 4) + {\rm{P}}(X = 5)\)
\({\text{P(pass)}} = 0.0579\) A1 N3
[6 marks]
(i) evidence of summing probabilities to 1 (M1)
e.g. \(0.67 + 0.05 + (a + 2b) + \ldots + 0.04 = 1\)
some simplification that clearly leads to required answer
e.g. \(0.76 + 4a + 2b = 1\) A1
\(4a + 2b = 0.24\) AG N0
(ii) correct substitution into the formula for expected value (A1)
e.g. \(0(0.67) + 1(0.05) + \ldots + 5(0.04)\)
some simplification (A1)
e.g. \(0.05 + 2a + 4b + \ldots + 5(0.04) = 1\)
correct equation A1
e.g. \(13a + 5b = 0.75\)
evidence of solving (M1)
\(a = 0.05\) , \(b = 0.02\) A1A1 N4
[8 marks]
attempt to find probability Bill passes (M1)
e.g. \({\rm{P}}(Y \ge 3)\)
correct value 0.19 A1
Bill (is more likely to pass) A1 N0
[3 marks]
Question
A box holds 240 eggs. The probability that an egg is brown is 0.05.
Find the expected number of brown eggs in the box.
Find the probability that there are 15 brown eggs in the box.
Find the probability that there are at least 10 brown eggs in the box.
Answer/Explanation
Markscheme
correct substitution into formula for \({\rm{E}}(X)\) (A1)
e.g. \(0.05 \times 240\)
\({\rm{E}}(X) = 12\) A1 N2
[2 marks]
evidence of recognizing binomial probability (may be seen in part (a)) (M1)
e.g. \(\left( {\begin{array}{*{20}{c}}
{240}\\
{15}
\end{array}} \right){(0.05)^{15}}{(0.95)^{225}}\) , \(X \sim {\rm{B}}(240,0.05)\)
\({\rm{P}}(X = 15) = 0.0733\) A1 N2
[2 marks]
\({\rm{P}}(X \le 9) = 0.236\) (A1)
evidence of valid approach (M1)
e.g. using complement, summing probabilities
\({\rm{P}}(X \ge 10) = 0.764\) A1 N3
[3 marks]
Question
Two fair 4-sided dice, one red and one green, are thrown. For each die, the faces are labelled 1, 2, 3, 4. The score for each die is the number which lands face down.
List the pairs of scores that give a sum of 6.
The probability distribution for the sum of the scores on the two dice is shown below.

Find the value of p , of q , and of r .
Fred plays a game. He throws two fair 4-sided dice four times. He wins a prize if the sum is 5 on three or more throws.
Find the probability that Fred wins a prize.
Markscheme
three correct pairs A1A1A1 N3
e.g. (2, 4), (3, 3), (4, 2) , R2G4, R3G3, R4G2
[3 marks]
\(p = \frac{1}{{16}}\) , \(q = \frac{2}{{16}}\) , \(r = \frac{2}{{16}}\) A1A1A1 N3
[3 marks]
let X be the number of times the sum of the dice is 5
evidence of valid approach (M1)
e.g. \(X \sim {\rm{B}}(n{\text{, }}p)\) , tree diagram, 5 sets of outcomes produce a win
one correct parameter (A1)
e.g. \(n = 4\) , \(p = 0.25\) , \(q = 0.75\)
Fred wins prize is \({\rm{P}}(X \ge 3)\) (A1)
appropriate approach to find probability M1
e.g. complement, summing probabilities, using a CDF function
correct substitution (A1)
e.g. \(1 – 0.949 \ldots \) , \(1 – \frac{{243}}{{256}}\) , \(0.046875 + 0.00390625\) , \(\frac{{12}}{{256}} + \frac{1}{{256}}\)
\({\text{probability of winning}} = 0.0508\) \(\left( {\frac{{13}}{{256}}} \right)\) A1 N3
[6 marks]
Question
A company produces a large number of water containers. Each container has two parts, a bottle and a cap. The bottles and caps are tested to check that they are not defective.
A cap has a probability of 0.012 of being defective. A random sample of 10 caps is selected for inspection.
Find the probability that exactly one cap in the sample will be defective.
The sample of caps passes inspection if at most one cap is defective. Find the probability that the sample passes inspection.
The heights of the bottles are normally distributed with a mean of \(22{\text{ cm}}\) and a standard deviation of \(0.3{\text{ cm}}\).
(i) Copy and complete the following diagram, shading the region representing where the heights are less than \(22.63{\text{ cm}}\).
(ii) Find the probability that the height of a bottle is less than \(22.63{\text{ cm}}\).
(i) A bottle is accepted if its height lies between \(21.37{\text{ cm}}\) and \(22.63{\text{ cm}}\). Find the probability that a bottle selected at random is accepted.
(ii) A sample of 10 bottles passes inspection if all of the bottles in the sample are accepted. Find the probability that the sample passes inspection.
The bottles and caps are manufactured separately. A sample of 10 bottles and a sample of 10 caps are randomly selected for testing. Find the probability that both samples pass inspection.
Answer/Explanation
Markscheme
Note: There may be slight differences in answers, depending on whether candidates use tables or GDCs, or their 3 sf answers in subsequent parts. Do not penalise answers that are consistent with their working and check carefully for FT.
evidence of recognizing binomial (seen anywhere in the question) (M1)
e.g. \(_n{C_r}{p^r}{q^{n – r}}\) , \({\text{B}}(n{\text{, }}p)\) , \(^{10}{C_1}{(0.012)^1}{(0.988)^9}\)
\(p = 0.108\) A1 N2
[2 marks]
valid approach (M1)
e.g. \({\rm{P}}(X \le 1)\) , \(0.88627 \ldots + 0.10764 \ldots \)
\(p = 0.994\) A1 N2
[2 marks]
(i)
 A1A1 N2
A1A1 N2
Note: Award A1 for vertical line to right of mean, A1 for shading to left of their vertical line.
(ii) valid approach (M1)
e.g. \({\rm{P}}(X < 22.63)\)
working to find standardized value (A1)
e.g. \(\frac{{22.63 – 22}}{{0.3}}\) , 2.1
\(p = 0.982\) A1 N3
[5 marks]
valid approach (M1)
e.g. \({\rm{P}}(21.37 < X < 22.63)\) , \({\rm{P}}( – 2.1 < z < 2.1)\)
correct working (A1)
e.g. \(0.982 – (1 – 0.982)\)
\(p = 0.964\) A1 N3
(ii) correct working (A1)
e.g. \(X \sim {\rm{B}}(10,0.964)\) , \({(0.964)^{10}}\)
\(p = 0.695\) (accept 0.694 from tables) A1 N2
[5 marks]
valid approach (M1)
e.g. \({\rm{P}}(A \cap B) = {\rm{P}}(A){\rm{P}}(B)\) , \((0.994) \times {(0.964)^{10}}\)
\(p = 0.691\) (accept \(0.690\) from tables) A1 N2
[2 marks]
Question
The probability of obtaining “tails” when a biased coin is tossed is \(0.57\). The coin is tossed ten times. Find the probability of obtaining at least four tails.
The probability of obtaining “tails” when a biased coin is tossed is 0.57. The coin is tossed ten times. Find the probability of obtaining the fourth tail on the tenth toss.
Answer/Explanation
Markscheme
evidence of recognizing binomial distribution (M1)
e.g. \(X \sim {\rm{B}}(10,0.57)\) , \(p = 0.57\) , \(q = 0.43\)
EITHER
\({\rm{P}}(X \le 3) = 2.16 \times {10^{ – 4}} + 0.00286 + 0.01709 + 0.06041\) \(( = 0.08057)\) (A1)
evidence of using complement (M1)
e.g. \(1 – \) any probability, \({\rm{P}}(X \ge 4) = 1 – {\rm{P}}(X \le 3)\)
\(0.919423 \ldots \)
\({\rm{P}}(X \ge 4) = 0.919\) A1 N3
OR
summing the probabilities from \(X = 4\) to \(X = 10\) (M1)
correct expression or values (A1)
e.g. \(\sum\limits_{r = 4}^{10} {\left( {\begin{array}{*{20}{c}}
{10}\\
r
\end{array}} \right)} {(0.57)^r}{(0.43)^{10 – r}}\) , \(0.14013 + 0.2229 + \ldots + 0.02731 + 0.00362\)
0.919424
\({\rm{P}}(X \ge 4) = 0.919\) A1 N3
[4 marks]
evidence of valid approach (M1)
e.g. three tails in nine tosses, \(\left( {\begin{array}{*{20}{c}}
9\\
3
\end{array}} \right){(0.57)^3}{(0.43)^6}\)
correct calculation
e.g. \(\left( {\begin{array}{*{20}{c}}
9\\
3
\end{array}} \right){(0.57)^3}{(0.43)^6} \times 0.57\) , \(0.09834 \times 0.57\) (A1)
\(0.05605178 \ldots \)
\({\text{P(4th tail on 10th toss)}} = 0.0561\) A1 N2
[3 marks]
Question
A factory makes lamps. The probability that a lamp is defective is 0.05. A random sample of 30 lamps is tested.
Find the probability that there is at least one defective lamp in the sample.
A factory makes lamps. The probability that a lamp is defective is 0.05. A random sample of 30 lamps is tested.
Given that there is at least one defective lamp in the sample, find the probability that there are at most two defective lamps.
Answer/Explanation
Markscheme
evidence of recognizing binomial (seen anywhere) (M1)
e.g. \({\rm{B}}(n{\text{, }}p)\), \({0.95^{30}}\)
finding \({\rm{P}}(X = 0) = 0.21463876\) (A1)
appropriate approach (M1)
e.g. complement, summing probabilities
\(0.785361\)
probability is \(0.785\) A1 N3
[4 marks]
identifying correct outcomes (seen anywhere) (A1)
e.g. \({\rm{P}}(X = 1) + {\rm{P}}(X = 2)\) , 1 or 2 defective, \(0.3389 \ldots + 0.2586 \ldots \)
recognizing conditional probability (seen anywhere) R1
e.g. \({\rm{P}}(A|B)\) , \({\rm{P}}(X \le 2|X \ge 1)\) , P(at most 2|at least 1)
appropriate approach involving conditional probability (M1)
e.g. \(\frac{{{\rm{P}}(X = 1) + {\rm{P}}(X = 2)}}{{{\rm{P}}(X \ge 1)}}\) , \(\frac{{0.3389 \ldots + 0.2586 \ldots }}{{0.785 \ldots }}\) , \(\frac{{1{\text{ or }}2}}{{0.785}}\)
\(0.760847\)
probability is \(0.761\) A1 N2
[4 marks]
Question
A bag contains four gold balls and six silver balls.
Two balls are drawn at random from the bag, with replacement. Let \(X\) be the number of gold balls drawn from the bag.
Fourteen balls are drawn from the bag, with replacement.
(i) Find \({\rm{P}}(X = 0)\) .
(ii) Find \({\rm{P}}(X = 1)\) .
(iii) Hence, find \({\rm{E}}(X)\) .
Hence, find \({\rm{E}}(X)\) .
Find the probability that exactly five of the balls are gold.
Find the probability that at most five of the balls are gold.
Given that at most five of the balls are gold, find the probability that exactly five of the balls are gold. Give the answer correct to two decimal places.
Answer/Explanation
Markscheme
METHOD 1
(i) appropriate approach (M1)
eg \(\frac{6}{{10}} \times \frac{6}{{10}}\) , \(\frac{6}{{10}} \times \frac{5}{9}\) , \(\frac{6}{{10}} \times \frac{5}{{10}}\)
\({\rm{P}}(X = 0) = \frac{9}{{25}} = 0.36\) A1 N2
(ii) multiplying one pair of gold and silver probabilities (M1)
eg \(\frac{6}{{10}} \times \frac{4}{{10}}\) , \(\frac{6}{{10}} \times \frac{4}{9}\) , 0.24
adding the product of both pairs of gold and silver probabilities (M1)
eg \(\frac{6}{{10}} \times \frac{4}{{10}} \times 2\) , \(\frac{6}{{10}} \times \frac{4}{9} + \frac{4}{{10}} \times \frac{6}{9}\)
\({\rm{P}}(X = 1) = \frac{{12}}{{25}} = 0.48\) A1 N3
(iii)
\({\rm{P}}(X = 2) = 0.16\) (seen anywhere) (A1)
correct substitution into formula for \({\rm{E}}(X)\) (A1)
eg \(0 \times 0.36 + 1 \times 0.48 + 2 \times 0.16\) , \(0.48 + 0.32\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
METHOD 2
(i) evidence of recognizing binomial (may be seen in part (ii)) (M1)
eg \(X \sim {\rm{B}}(2,0.6)\) , \(\left( \begin{array}{l}
2\\
0
\end{array} \right){(0.4)^2}{(0.6)^0}\)
correct probability for use in binomial (A1)
eg \(p = 0.4\) , \(X \sim {\rm{B}}(2,0.4)\) , \(^2{C_0}{(0.4)^0}{(0.6)^2}\)
\({\rm{P}}(X = 0) = \frac{9}{{25}} = 0.36\) A1 N3
(ii) correct set up (A1)
eg \(_2{C_1}{(0.4)^1}{(0.6)^1}\)
\({\rm{P}}(X = 1) = \frac{{12}}{{25}} = 0.48\) A1 N2
(iii)
attempt to substitute into \(np\) (M1)
eg \(2 \times 0.6\)
correct substitution into \(np\) (A1)
eg \(2 \times 0.4\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
[8 marks]
METHOD 1
\({\rm{P}}(X = 2) = 0.16\) (seen anywhere) (A1)
correct substitution into formula for \({\rm{E}}(X)\) (A1)
eg \(0 \times 0.36 + 1 \times 0.48 + 2 \times 0.16\) , \(0.48 + 0.32\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
METHOD 2
attempt to substitute into \(np\) (M1)
eg \(2 \times 0.6\)
correct substitution into \(np\) (A1)
eg \(2 \times 0.4\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
[3 marks]
Let \(Y\) be the number of gold balls drawn from the bag.
evidence of recognizing binomial (seen anywhere) (M1)
eg \(_{14}{C_5}{(0.4)^5}{(0.6)^9}\) , \({\rm{B}}(14,0.4)\)
\({\rm{P}}(Y = 5) = 0.207\) A1 N2
[2 marks]
recognize need to find \({\rm{P}}(Y \le 5)\) (M1)
\({\rm{P}}(Y \le 5) = 0.486\) A1 N2
[2 marks]
Let \(Y\) be the number of gold balls drawn from the bag.
recognizing conditional probability (M1)
eg \({\rm{P}}(A|B)\) , \({\rm{P}}(Y = 5|Y \le 5)\) , \(\frac{{{\rm{P}}(Y = 5)}}{{{\rm{P}}(Y \le 5)}}\) , \(\frac{{0.207}}{{0.486}}\)
\({\rm{P}}(Y = 5|Y \le 5) = 0.42522518\) (A1)
\({\rm{P}}(Y = 5|Y \le 5) = 0.43\) (to \(2\) dp) A1 N2
[3 marks]
Question
Samantha goes to school five days a week. When it rains, the probability that she goes to school by bus is 0.5. When it does not rain, the probability that she goes to school by bus is 0.3. The probability that it rains on any given day is 0.2.
On a randomly selected school day, find the probability that Samantha goes to school by bus.
Given that Samantha went to school by bus on Monday, find the probability that it was raining.
In a randomly chosen school week, find the probability that Samantha goes to school by bus on exactly three days.
After \(n\) school days, the probability that Samantha goes to school by bus at least once is greater than \(0.95\). Find the smallest value of \(n\).
Answer/Explanation
Markscheme
appropriate approach (M1)
eg \({\text{P}}(R \cap B) + {\text{P}}(R’ \cap B)\), tree diagram,
one correct multiplication (A1)
eg \(0.2 \times 0.5,{\text{ }}0.24\)
correct working (A1)
eg \(0.2 \times 0.5 + 0.8 \times 0.3,{\text{ }}0.1 + 0.24\)
\({\text{P(bus)}} = 0.34 {\text{(exact)}}\) A1 N3
[4 marks]
recognizing conditional probability (R1)
eg \({\text{P}}(A|B) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\)
correct working A1
eg \(\frac{{0.2 \times 0.5}}{{0.34}}\)
\({\text{P}}(R|B) = \frac{5}{{17}},{\text{ }}0.294\) A1 N2
[3 marks]
recognizing binomial probability (R1)
eg \(X \sim {\text{B}}(n,{\text{ }}p)\), \(\left( \begin{array}{c}5\\3\end{array} \right)\) \({(0.34)^3},{\text{ }}{(0.34)^3}{(1 – 0.34)^2}\)
\({\text{P}}(X = 3) = 0.171\) A1 N2
[2 marks]
METHOD 1
evidence of using complement (seen anywhere) (M1)
eg \(1 – {\text{P (none), }}1 – 0.95\)
valid approach (M1)
eg \(1 – {\text{P (none)}} > 0.95,{\text{ P (none)}} < 0.05,{\text{ }}1 – {\text{P (none)}} = 0.95\)
correct inequality (accept equation) A1
eg \(1 – {(0.66)^n} > 0.95,{\text{ }}{(0.66)^n} = 0.05\)
\(n > 7.209{\text{ (accept }}n = 7.209{\text{)}}\) (A1)
\(n = 8\) A1 N3
METHOD 2
valid approach using guess and check/trial and error (M1)
eg finding \({\text{P}}(X \geqslant 1)\) for various values of n
seeing the “cross over” values for the probabilities A1A1
\(n = 7,{\text{ P}}(X \geqslant 1) = 0.9454,{\text{ }}n = 8,{\text{ P}}(X \geqslant 1) = 0.939\)
recognising \(0.9639 > 0.95\) (R1)
\(n = 8\) A1 N3
[5 marks]
Question
A forest has a large number of tall trees. The heights of the trees are normally distributed with a mean of \(53\) metres and a standard deviation of \(8\) metres. Trees are classified as giant trees if they are more than \(60\) metres tall.
A tree is selected at random from the forest.
Find the probability that this tree is a giant.
A tree is selected at random from the forest.
Given that this tree is a giant, find the probability that it is taller than \(70\) metres.
Two trees are selected at random. Find the probability that they are both giants.
\(100\) trees are selected at random.
Find the expected number of these trees that are giants.
\(100\) trees are selected at random.
Find the probability that at least \(25\) of these trees are giants.
Answer/Explanation
Markscheme
valid approach (M1)
eg \({\text{P}}(G) = {\text{P}}(H > 60,{\text{ }}z = 0.875,{\text{ P}}(H > 60) = 1 – 0.809,{\text{ N}}\left( {53, {8^2}} \right)\)
\(0.190786\)
\({\text{P}}(G) = 0.191\) A1 N2
[3 marks]
finding \({\text{P}}(H > 70) = 0.01679\) (seen anywhere) (A1)
recognizing conditional probability (R1)
eg \({\text{P}}(A\left| {B),{\text{ P}}(H > 70\left| {H > 60)} \right.} \right.\)
correct working (A1)
eg \(\frac{{0.01679}}{{0.191}}\)
\(0.0880209\)
\({\text{P}}(X > 70\left| {G) = 0.0880} \right.\) A1 N3
[6 marks]
attempt to square their \({\text{P}}(G)\) (M1)
eg \({0.191^2}\)
\(0.0363996\)
\({\text{P}}({\text{both }}G) = 0.0364\) A1 N2
[2 marks]
correct substitution into formula for \({\text{E}}(X)\) (A1)
eg \(100(0.191)\)
\({\text{E}}(G) = 19.1{\text{ }}[19.0,{\text{ }}19.1]\) A1 N2
[3 marks]
recognizing binomial probability (may be seen in part (c)(i)) (R1)
eg \(X \sim {\text{B}}(n,{\text{ }}p)\)
valid approach (seen anywhere) (M1)
eg \({\text{P}}(X \geqslant 25) = 1 – {\text{P}}(X \leqslant 24),{\text{ }}1 – {\text{P}}(X < a)\)
correct working (A1)
eg \({\text{P}}(X \leqslant 24) = 0.913 \ldots ,{\text{ }}1 – 0.913 \ldots \)
\(0.0869002\)
\({\text{P}}(X \geqslant 25) = 0.0869\) A1 N2
[3 marks]
Question
A company makes containers of yogurt. The volume of yogurt in the containers is normally distributed with a mean of \(260\) ml and standard deviation of \(6\) ml.
A container which contains less than \(250\) ml of yogurt is underfilled.
A container is chosen at random. Find the probability that it is underfilled.
The company decides that the probability of a container being underfilled should be reduced to \(0.02\). It decreases the standard deviation to \(\sigma \) and leaves the mean unchanged.
Find \(\sigma \).
The company changes to the new standard deviation, \(\sigma \), and leaves the mean unchanged.
A container is chosen at random for inspection. It passes inspection if its volume of yogurt is between \(250\) and \(271\) ml.
(i) Find the probability that it passes inspection.
(ii) Given that the container is not underfilled, find the probability that it passes inspection.
A sample of \(50\) containers is chosen at random. Find the probability that \(48\) or more of the containers pass inspection.
Answer/Explanation
Markscheme
\(0.0477903\)
probability \( = 0.0478\) A2 N2
[2 marks]
\({\text{P}}({\text{volume}} < 250) = 0.02\) (M1)
\(z = – 2.05374\;\;\;\)(may be seen in equation) A1
attempt to set up equation with \(z\) (M1)
eg\(\;\;\;\frac{{\mu – 260}}{\sigma } = z,{\text{ }}260 – 2.05(\sigma ) = 250\)
\(4.86914\)
\(\sigma = 4.87{\text{ (ml)}}\) A1 N3
[4 marks]
(i) \(0.968062\)
\({\text{P}}(250 < {\text{Vol}} < 271) = 0.968\) A2 N2
(ii) recognizing conditional probability (seen anywhere, including in correct working) R1
eg\(\;\;\;{\text{P}}(A|B),{\text{ }}\frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}},{\text{ P}}(A \cap B) = {\text{P}}(A|B){\text{P}}(B)\)
correct value or expression for \(P\) (not underfilled) (A1)
eg\(\;\;\;0.98,1 – 0.02,{\text{ }}1 – {\text{P}}(X < 250)\)
probability \( = \frac{{0.968}}{{0.98}}\) A1
\(0.987818\)
probability \( = 0.988\) A1 N2
[6 marks]
METHOD 1
evidence of recognizing binomial distribution (seen anywhere) (M1)
eg\(\;\;\;X\;\;\;{\text{B}}(50,{\text{ }}0.968),{\text{ binomial cdf, }}p = 0.968,{\text{ }}r = 47\)
\({\text{P}}(X \le 47\)) = 0.214106\) (A1)
evidence of using complement (M1)
eg\(\;\;\;1 – {\text{P}}(X \le 47\))
\(0.785894\)
probability \( = 0.786\) A1 N3
METHOD 2
evidence of recognizing binomial distribution (seen anywhere) (M1)
eg\(\;\;\;X\;\;\;{\text{B}}(50,{\text{ }}0.968),{\text{ binomial cdf, }}p = 0.968,{\text{ }}r = 47\)
\({\text{P(not pass)}} = 1 – {\text{P(pass)}} = 0.0319378\) (A1)
evidence of attempt to find \(P\) (\(2\) or fewer fail) (M1)
eg\(\;\;\;\)\(0\), \(1\), or \(2\) not pass, \({\text{B}}(50,{\text{ }}2)\)
\(0.785894\)
probability \( = 0.786\) A1 N3
METHOD 3
evidence of recognizing binomial distribution (seen anywhere) (M1)
eg\(\;\;\;X\;\;\;{\text{B}}(50,{\text{ }}0.968),{\text{ binomial cdf, }}p = 0.968,{\text{ }}r = 47\)
evidence of summing probabilities (M1)
eg\(\;\;\;{\text{P}}(X = 48) + {\text{P}}(X = 49) + {\text{P}}(X = 50)\)
correct working
eg\(\;\;\;0.263088 + 0.325488 + 0.197317\) (A1)
\(0.785894\)
probability \( = 0.786\) A1 N3
[4 marks]
Total [16 marks]
Question
A factory has two machines, A and B. The number of breakdowns of each machine is independent from day to day.
Let \(A\) be the number of breakdowns of Machine A on any given day. The probability distribution for \(A\) can be modelled by the following table.

Let \(B\) be the number of breakdowns of Machine B on any given day. The probability distribution for \(B\) can be modelled by the following table.

On Tuesday, the factory uses both Machine A and Machine B. The variables \(A\) and \(B\) are independent.
Find \(k\).
(i) A day is chosen at random. Write down the probability that Machine A has no breakdowns.
(ii) Five days are chosen at random. Find the probability that Machine A has no breakdowns on exactly four of these days.
Find \({\text{E}}(B)\).
(i) Find the probability that there are exactly two breakdowns on Tuesday.
(ii) Given that there are exactly two breakdowns on Tuesday, find the probability that both breakdowns are of Machine A.
Answer/Explanation
Markscheme
evidence of summing to 1 (M1)
eg\(\,\,\,\,\,\)\(0.55 + 0.3 + 0.1 + k = 1\)
\(k = 0.05{\text{ (exact)}}\) A1 N2
[2 marks]
(i) 0.55 A1 N1
(ii) recognizing binomial probability (M1)
eg\(\,\,\,\,\,\)\(X:{\text{ }}B(n,{\text{ }}p),{\text{ }}\left( {\begin{array}{*{20}{c}} 5 \\ 4 \end{array}} \right),{\text{ }}{(0.55)^4}(1 – 0.55),{\text{ }}\left( {\begin{array}{*{20}{c}} n \\ r \end{array}} \right){p^r}{q^{n – r}}\)
\(P(X = 4) = 0.205889\)
\(P(X = 4) = 0.206\) A1 N2
[3 marks]
correct substitution into formula for \({\text{E}}(X)\) (A1)
eg\(\,\,\,\,\,\)\(0.2 + (2 \times 0.08) + (3 \times 0.02)\)
\({\text{E}}(B) = 0.42{\text{ (exact)}}\) A1 N2
[2 marks]
(i) valid attempt to find one possible way of having 2 breakdowns (M1)
eg\(\,\,\,\,\,\)\(2A,{\text{ }}2B,{\text{ }}1A\) and \(1B\), tree diagram
one correct calculation for 1 way (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\(0.1 \times 0.7,{\text{ }}0.55 \times 0.08,{\text{ }}0.3 \times 0.2\)
recognizing there are 3 ways of having 2 breakdowns (M1)
eg\(\,\,\,\,\,\)A twice or B twice or one breakdown each
correct working (A1)
eg\(\,\,\,\,\,\)\((0.1 \times 0.7) + (0.55 \times 0.08) + (0.3 \times 0.2)\)
\({\text{P(2 breakdowns)}} = 0.174{\text{ (exact)}}\) A1 N3
(ii) recognizing conditional probability (M1)
eg\(\,\,\,\,\,\)\({\text{P}}(A|B),{\text{ P}}(2A|{\text{2breakdowns}})\)
correct working (A1)
eg\(\,\,\,\,\,\)\(\frac{{0.1 \times 0.7}}{{0.174}}\)
\({\text{P}}(A = 2|{\text{two breakdowns}}) = 0.402298\)
\({\text{P}}(A = 2|{\text{two breakdowns}}) = 0.402\) A1 N2
[8 marks]
Question
A jar contains 5 red discs, 10 blue discs and \(m\) green discs. A disc is selected at random and replaced. This process is performed four times.
Write down the probability that the first disc selected is red.
Let \(X\) be the number of red discs selected. Find the smallest value of \(m\) for which \({\text{Var}}(X{\text{ }}) < 0.6\).
Markscheme
\({\text{P(red)}} = \frac{5}{{15 + m}}\) A1 N1
[1 mark]
recognizing binomial distribution (M1)
eg\(\,\,\,\,\,\)\(X \sim B(n,{\text{ }}p)\)
correct value for the complement of their \(p\) (seen anywhere) A1
eg\(\,\,\,\,\,\)\(1 – \frac{5}{{15 + m}},{\text{ }}\frac{{10 + m}}{{15 + m}}\)
correct substitution into \({\text{Var}}(X) = np(1 – p)\) (A1)
eg\(\,\,\,\,\,\)\(4\left( {\frac{5}{{15 + m}}} \right)\left( {\frac{{10 + m}}{{15 + m}}} \right),{\text{ }}\frac{{20(10 + m)}}{{{{(15 + m)}^2}}} < 0.6\)
\(m > 12.2075\) (A1)
\(m = 13\) A1 N3
[5 marks]
Question
Adam is a beekeeper who collected data about monthly honey production in his bee hives. The data for six of his hives is shown in the following table.

The relationship between the variables is modelled by the regression line with equation \(P = aN + b\).
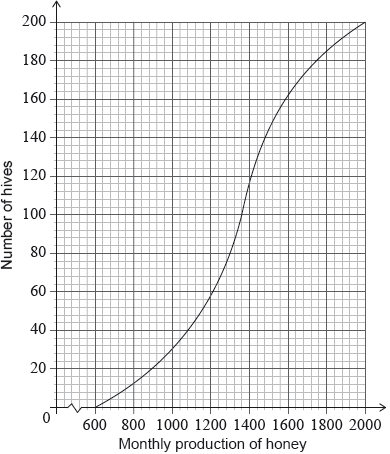
Adam has 200 hives in total. He collects data on the monthly honey production of all the hives. This data is shown in the following cumulative frequency graph.
Adam’s hives are labelled as low, regular or high production, as defined in the following table.

Adam knows that 128 of his hives have a regular production.
Write down the value of \(a\) and of \(b\).
Use this regression line to estimate the monthly honey production from a hive that has 270 bees.
Write down the number of low production hives.
Find the value of \(k\);
Find the number of hives that have a high production.
Adam decides to increase the number of bees in each low production hive. Research suggests that there is a probability of 0.75 that a low production hive becomes a regular production hive. Calculate the probability that 30 low production hives become regular production hives.
Answer/Explanation
Markscheme
evidence of setup (M1)
eg\(\,\,\,\,\,\)correct value for \(a\) or \(b\)
\(a = 6.96103,{\text{ }}b = – 454.805\)
\(a = 6.96,{\text{ }}b = – 455{\text{ (accept }}6.96x – 455)\) A1A1 N3
[3 marks]
substituting \(N = 270\) into their equation (M1)
eg\(\,\,\,\,\,\)\(6.96(270) – 455\)
1424.67
\(P = 1420{\text{ (g)}}\) A1 N2
[2 marks]
40 (hives) A1 N1
[1 mark]
valid approach (M1)
eg\(\,\,\,\,\,\)\(128 + 40\)
168 hives have a production less than \(k\) (A1)
\(k = 1640\) A1 N3
[3 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(200 – 168\)
32 (hives) A1 N2
[2 marks]
recognize binomial distribution (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(X \sim {\text{B}}(n,{\text{ }}p),{\text{ }}\left( {\begin{array}{*{20}{c}} n \\ r \end{array}} \right){p^r}{(1 – p)^{n – r}}\)
correct values (A1)
eg\(\,\,\,\,\,\)\(n = 40\) (check FT) and \(p = 0.75\) and \(r = 30,{\text{ }}\left( {\begin{array}{*{20}{c}} {40} \\ {30} \end{array}} \right){0.75^{30}}{(1 – 0.75)^{10}}\)
0.144364
0.144 A1 N2
[3 marks]
Question
The weights, in grams, of oranges grown in an orchard, are normally distributed with a mean of 297 g. It is known that 79 % of the oranges weigh more than 289 g and 9.5 % of the oranges weigh more than 310 g.
The weights of the oranges have a standard deviation of σ.
The grocer at a local grocery store will buy the oranges whose weights exceed the 35th percentile.
The orchard packs oranges in boxes of 36.
Find the probability that an orange weighs between 289 g and 310 g.
Find the standardized value for 289 g.
Hence, find the value of σ.
To the nearest gram, find the minimum weight of an orange that the grocer will buy.
Find the probability that the grocer buys more than half the oranges in a box selected at random.
The grocer selects two boxes at random.
Find the probability that the grocer buys more than half the oranges in each box.
Answer/Explanation
Markscheme
correct approach indicating subtraction (A1)
eg 0.79 − 0.095, appropriate shading in diagram
P(289 < w < 310) = 0.695 (exact), 69.5 % A1 N2
[2 marks]
METHOD 1
valid approach (M1)
eg 1 − p, 21
−0.806421
z = −0.806 A1 N2
METHOD 2
(i) & (ii)
correct expression for z (seen anywhere) (A1)
eg \(\frac{{289 – u}}{\sigma }\)
valid approach (M1)
eg 1 − p, 21
−0.806421
z = −0.806 (seen anywhere) A1 N2
[2 marks]
METHOD 1
attempt to standardize (M1)
eg \(\sigma = \frac{{289 – 297}}{z},\,\,\frac{{289 – 297}}{\sigma }\)
correct substitution with their z (do not accept a probability) A1
eg \( – 0.806 = \frac{{289 – 297}}{\sigma },\,\,\frac{{289 – 297}}{{ – 0.806}}\)
9.92037
σ = 9.92 A1 N2
METHOD 2
(i) & (ii)
correct expression for z (seen anywhere) (A1)
eg \(\frac{{289 – u}}{\sigma }\)
valid approach (M1)
eg 1 − p, 21
−0.806421
z = −0.806 (seen anywhere) A1 N2
valid attempt to set up an equation with their z (do not accept a probability) (M1)
eg \( – 0.806 = \frac{{289 – 297}}{\sigma },\,\,\frac{{289 – 297}}{{ – 0.806}}\)
9.92037
σ = 9.92 A1 N2
[3 marks]
valid approach (M1)
eg P(W < w) = 0.35, −0.338520 (accept 0.385320), diagram showing values in a standard normal distribution
correct score at the 35th percentile (A1)
eg 293.177
294 (g) A1 N2
Note: If working shown, award (M1)(A1)A0 for 293.
If no working shown, award N1 for 293.177, N1 for 293.
Exception to the FT rule: If the score is incorrect, and working shown, award A1FT for correctly finding their minimum weight (by rounding up)
[3 marks]
evidence of recognizing binomial (seen anywhere) (M1)
eg \(X \sim {\text{B}}\left( {36,\,\,p} \right),\,\,{}_n{C_a} \times {p^a} \times {q^{n – a}}\)
correct probability (seen anywhere) (A1)
eg 0.65
EITHER
finding P(X ≤ 18) from GDC (A1)
eg 0.045720
evidence of using complement (M1)
eg 1−P(X ≤ 18)
0.954279
P(X > 18) = 0.954 A1 N2
OR
recognizing P(X > 18) = P(X ≥ 19) (M1)
summing terms from 19 to 36 (A1)
eg P(X = 19) + P(X = 20) + … + P(X = 36)
0.954279
P(X > 18) = 0.954 A1 N2
[5 marks]
correct calculation (A1)
\({0.954^2},\,\,\left( \begin{gathered}
2 \hfill \\
2 \hfill \\
\end{gathered} \right){0.954^2}{\left( {1 – 0.954} \right)^0}\)
0.910650
0.911 A1 N2
[2 marks]
Question
The mass M of apples in grams is normally distributed with mean μ. The following table shows probabilities for values of M.
The apples are packed in bags of ten.
Any apples with a mass less than 95 g are classified as small.
Write down the value of k.
Show that μ = 106.
Find P(M < 95) .
Find the probability that a bag of apples selected at random contains at most one small apple.
Find the expected number of bags in this crate that contain at most one small apple.
Find the probability that at least 48 bags in this crate contain at most one small apple.
Answer/Explanation
Markscheme
evidence of using \(\sum {{p_i}} = 1\) (M1)
eg k + 0.98 + 0.01 = 1
k = 0.01 A1 N2
[2 marks]
recognizing that 93 and 119 are symmetrical about μ (M1)
eg μ is midpoint of 93 and 119
correct working to find μ A1
\(\frac{{119 + 93}}{2}\)
μ = 106 AG N0
[2 marks]
finding standardized value for 93 or 119 (A1)
eg z = −2.32634, z = 2.32634
correct substitution using their z value (A1)
eg \(\frac{{93 – 106}}{\sigma } = – 2.32634,\,\,\frac{{119 – 106}}{{2.32634}} = \sigma \)
σ = 5.58815 (A1)
0.024508
P(X < 95) = 0.0245 A2 N3
[5 marks]
evidence of recognizing binomial (M1)
eg 10, ananaCpqn−=××and 0.024B(5,,)pnp=
valid approach (M1)
eg P(1),P(0)P(1)XXX≤=+=
0.976285
0.976 A1 N2
[3 marks]
recognizing new binomial probability (M1)
eg B(50, 0.976)
correct substitution (A1)
eg E(X) = 50 (0.976285)
48.81425
48.8 A1 N2
[3 marks]
valid approach (M1)
eg P(X ≥ 48), 1 − P(X ≤ 47)
0.884688
0.885 A1 N2
[2 marks]
Question
The probability of obtaining heads on a biased coin is 0.4. The coin is tossed 600 times.
(i) Write down the mean number of heads.
(ii) Find the standard deviation of the number of heads.
Find the probability that the number of heads obtained is less than one standard deviation away from the mean.
Answer/Explanation
Markscheme
(i) recognizing binomial with \(n = 600\) , \(p = 0.4\) M1
\({\rm{E}}(X) = 240\) A1 N2
(ii) correct substitution into formula for variance or standard deviation A1
e.g. 144, \(\sqrt {600 \times 0.4 \times 0.6} \)
sd = 12 A1 N1
[4 marks]
attempt to find range of values M1
e.g. \(240 \pm 12\) \(228 < X < 252\)
evidence of correct approach A1
e.g. \({\rm{P}}(X \le 251) – {\rm{P}}(X \le 228)\)
\({\rm{P}}(228 < X < 252) = 0.662\) A1 N2
[3 marks]

