Download IITian Academy App for accessing Online Mock Tests and More..
Question
A box contains a large number of biscuits. The weights of biscuits are normally distributed with mean \(7{\text{ g}}\) and standard deviation \(0.5{\text{ g}}\) .
One biscuit is chosen at random from the box. Find the probability that this biscuit
(i) weighs less than \(8{\text{ g}}\) ;
(ii) weighs between \(6{\text{ g}}\) and \(8{\text{ g}}\) .
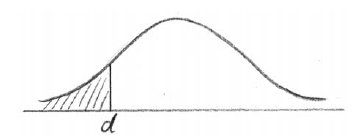
Five percent of the biscuits in the box weigh less than d grams.
(i) Copy and complete the following normal distribution diagram, to represent this information, by indicating d, and shading the appropriate region.
(ii) Find the value of d.
The weights of biscuits in another box are normally distributed with mean \(\mu \) and standard deviation \(0.5{\text{ g}}\). It is known that \(20\% \) of the biscuits in this second box weight less than \(5{\text{ g}}\).
Find the value of \(\mu \) .
Answer/Explanation
Markscheme
\(X \sim {\text{N}}(7{\text{, }}{0.5^2})\)
(i) \(z = 2\) (M1)
\({\rm{P}}(X < 8) = {\rm{P}}(Z < 2) = 0.977\) A1 N2
(ii) evidence of appropriate approach (M1)
e.g. symmetry, \(z = – 2\)
\({\rm{P}}(6 < X < 8) = 0.954\) (tables 0.955) A1 N2
Note: Award M1A1(AP) if candidates refer to 2 standard deviations from the mean, leading to 0.95.
[4 marks]
(i)
A1A1 N2
Note: Award A1 for d to the left of the mean, A1 for area to the left of d shaded.
(ii) \(z = – 1.645\) (A1)
\(\frac{{d – 7}}{{0.5}} = – 1.645\) (M1)
\(d = 6.18\) A1 N3
[5 marks]
\(Y \sim {\text{N}}(\mu {\text{, }}{0.5^2})\)
\({\rm{P}}(Y < 5) = 0.2\) (M1)
\(z = – 0.84162 \ldots \) A1
\(\frac{{5 – \mu }}{{0.5}} = – 0.8416\) (M1)
\(\mu = 5.42\) A1 N3
[4 marks]
Question
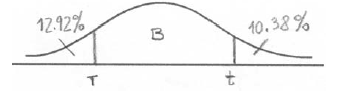
The heights of certain plants are normally distributed. The plants are classified into three categories.
The shortest \(12.92\% \) are in category A.
The tallest \(10.38\% \) are in category C.
All the other plants are in category B with heights between \(r{\text{ cm}}\) and \(t{\text{ cm}}\) .
Complete the following diagram to represent this information.
Given that the mean height is \(6.84{\text{ cm}}\) and the standard deviation \(0.25{\text{ cm}}\) , find the value of r and of t.
Answer/Explanation
Markscheme
A1A1 N2
Notes: Award A1 for three regions (may be shown by lines or shading), A1 for clear labelling of two regions (may be shown by percentages or categories). r and t need not be labelled, but if they are, they may be interchanged.
[2 marks]
METHOD 1
\({\rm{P}}(X < r) = 0.1292\) (A1)
\(r = 6.56\) A1 N2
\(1 – 0.1038\) (= 0.8962) (may be seen later) A1
\({\rm{P}}(X < t) = 0.8962\) (A1)
\(t = 7.16\) A1 N2
METHOD 2
finding z-values \( – 1.130 \ldots{\text{, }}1.260 \ldots \) A1A1
evidence of setting up one standardised equation (M1)
e.g. \(\frac{{r – 6.84}}{{0.25}} = – 1.13 \ldots \) , \(t = 1.260 \times 0.25 + 6.84\)
\(r = 6.56\) , \(t = 7.16\) A1A1 N2N2
[5 marks]
Question
The scores of a test given to students are normally distributed with a mean of 21. \(80\% \) of the students have scores less than 23.7.
Find the standard deviation of the scores.
A student is chosen at random. This student has the same probability of having a score less than 25.4 as having a score greater than b.
(i) Find the probability the student has a score less than 25.4.
(ii) Find the value of b.
Answer/Explanation
Markscheme
evidence of approach (M1)
e.g. finding \(0.84 \ldots \), using \(\frac{{23.7 – 21}}{\sigma }\)
correct working (A1)
e.g. \(0.84 \ldots = \frac{{23.7 – 21}}{\sigma }\) , graph A1
\(\sigma = 3.21\)
[3 marks]
(i) evidence of attempting to find \({\text{P}}(X < 25.4)\) (M1)
e.g. using \(z = 1.37\)
\({\text{P}}(X < 25.4) = 0.915\) A1 N2
(ii) evidence of recognizing symmetry (M1)
e.g. \(b = 21 – 4.4\) , using \(z = – 1.37\) A1 N2
[4 marks]
Question
A random variable X is distributed normally with mean 450 and standard deviation 20.
Find \({\rm{P}}(X \le 475)\) .
Given that \({\rm{P}}(X > a) = 0.27\) , find \(a\).
Answer/Explanation
Markscheme
evidence of attempt to find \({\rm{P}}(X \le 475)\) (M1)
e.g. \({\rm{P}}(Z \le 1.25)\)
\({\rm{P}}(X \le 475) = 0.894\) A1 N2
[2 marks]
evidence of using the complement (M1)
e.g. 0.73, \(1 – p\)
\(z = 0.6128\) (A1)
setting up equation (M1)
e.g. \(\frac{{a – 450}}{{20}} = 0.6128\)
\(a = 462\) A1 N3
[4 marks]
Question
A van can take either Route A or Route B for a particular journey.
If Route A is taken, the journey time may be assumed to be normally distributed with mean 46 minutes and a standard deviation 10 minutes.
If Route B is taken, the journey time may be assumed to be normally distributed with mean \(\mu \) minutes and standard deviation 12 minutes.
For Route A, find the probability that the journey takes more than \(60\) minutes.
For Route B, the probability that the journey takes less than \(60\) minutes is \(0.85\).
Find the value of \(\mu \) .
The van sets out at 06:00 and needs to arrive before 07:00.
(i) Which route should it take?
(ii) Justify your answer.
On five consecutive days the van sets out at 06:00 and takes Route B. Find the probability that
(i) it arrives before 07:00 on all five days;
(ii) it arrives before 07:00 on at least three days.
Answer/Explanation
Markscheme
\(A \sim N(46{\text{, }}{10^2})\) \(B \sim N(\mu {\text{, }}{12^2})\)
\({\rm{P}}(A > 60) = 0.0808\) A2 N2
[2 marks]
correct approach (A1)
e.g. \({\rm{P}}\left( {Z < \frac{{60 – \mu }}{{12}}} \right) = 0.85\) , sketch
\(\frac{{60 – \mu }}{{12}} = 1.036 \ldots \) (A1)
\(\mu = 47.6\) A1 N2
[3 marks]
(i) route A A1 N1
(ii) METHOD 1
\({\rm{P}}(A < 60) = 1 – 0.0808 = 0.9192\) A1
valid reason R1
e.g. probability of A getting there on time is greater than probability of B
\(0.9192 > 0.85\) N2
METHOD 2
\({\rm{P}}(B > 60) = 1 – 0.85 = 0.15\) A1
valid reason R1
e.g. probability of A getting there late is less than probability of B
\(0.0808 < 0.15\) N2
[3 marks]
(i) let X be the number of days when the van arrives before 07:00
\({\rm{P}}(X = 5) = {(0.85)^5}\) (A1)
\( = 0.444\) A1 N2
(ii) METHOD 1
evidence of adding correct probabilities (M1)
e.g. \({\rm{P}}(X \ge 3) = {\rm{P}}(X = 3) + {\rm{P}}(X = 4) + {\rm{P}}(X = 5)\)
correct values \(0.1382 + 0.3915 + 0.4437\) (A1)
\({\rm{P}}(X \ge 3) = 0.973\) A1 N3
METHOD 2
evidence of using the complement (M1)
e.g. \({\rm{P}}(X \ge 3) = 1 – {\rm{P}}(X \le 2)\) , \(1 – p\)
correct values \(1 – 0.02661\) (A1)
\({\rm{P}}(X \ge 3) = 0.973\) A1 N3
[5 marks]
Question
The weights of players in a sports league are normally distributed with a mean of \(76.6{\text{ kg}}\), (correct to three significant figures). It is known that \(80\% \) of the players have weights between \(68{\text{ kg}}\) and \(82{\text{ kg}}\). The probability that a player weighs less than \(68{\text{ kg}}\) is 0.05.
Find the probability that a player weighs more than \(82{\text{ kg}}\).
(i) Write down the standardized value, z, for \(68{\text{ kg}}\).
(ii) Hence, find the standard deviation of weights.
To take part in a tournament, a player’s weight must be within 1.5 standard deviations of the mean.
(i) Find the set of all possible weights of players that take part in the tournament.
(ii) A player is selected at random. Find the probability that the player takes part in the tournament.
Of the players in the league, \(25\% \) are women. Of the women, \(70\% \) take part in the tournament.
Given that a player selected at random takes part in the tournament, find the probability that the selected player is a woman.
Answer/Explanation
Markscheme
evidence of appropriate approach (M1)
e.g. \(1 – 0.85\) , diagram showing values in a normal curve
\({\rm{P}}(w \ge 82) = 0.15\) A1 N2
[2 marks]
(i) \(z = – 1.64\) A1 N1
(ii) evidence of appropriate approach (M1)
e.g. \( – 1.64 = \frac{{x – \mu }}{\sigma }\) , \(\frac{{68 – 76.6}}{\sigma }\)
correct substitution A1
e.g. \( – 1.64 = \frac{{68 – 76.6}}{\sigma }\)
\(\sigma = 5.23\) A1 N1
[4 marks]
(i) \(68.8 \le {\rm{weight}} \le 84.4\) A1A1A1 N3
Note: Award A1 for 68.8, A1 for 84.4, A1 for giving answer as an interval.
(ii) evidence of appropriate approach (M1)
e.g. \({\rm{P}}( – 1.5 \le z \le 1.5)\) , \({\rm{P}}(68.76 < y < 84.44)\)
\({\text{P(qualify)}} = 0.866\) A1 N2
[5 marks]
recognizing conditional probability (M1)
e.g. \({\rm{P}}(A|B) = \frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}}\)
\({\rm{P}}({\text{woman and qualify}}) = 0.25 \times 0.7\) (A1)
\({\rm{P}}({\rm{woman}}|{\rm{qualify}}) = \frac{{0.25 \times 0.7}}{{0.866}}\) A1
\({\rm{P}}({\rm{woman}}|{\rm{qualify}}) = 0.202\) A1
[4 marks]
Question
A random variable X is distributed normally with a mean of 20 and variance 9.
Find \({\rm{P}}(X \le 24.5)\) .
Let \({\rm{P}}(X \le k) = 0.85\) .
(i) Represent this information on the following diagram.
(ii) Find the value of k .
Answer/Explanation
Markscheme
\(\sigma = 3\) (A1)
evidence of attempt to find \({\rm{P}}(X \le 24.5)\) (M1)
e.g. \(z = 1.5\) , \(\frac{{24.5 – 20}}{3}\)
\({\rm{P}}(X \le 24.5) = 0.933\) A1 N3
[3 marks]
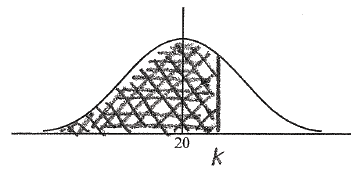A1A1 N2
Note: Award A1 with shading that clearly extends to right of the mean, A1 for any correct label, either k, area or their value of k.
(ii) \(z = 1.03(64338)\) (A1)
attempt to set up an equation (M1)
e.g. \(\frac{{k – 20}}{3} = 1.0364\) , \(\frac{{k – 20}}{3} = 0.85\)
\(k = 23.1\) A1 N3
[5 marks]
Question
Let the random variable X be normally distributed with mean 25, as shown in the following diagram.
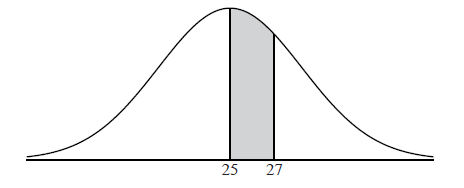
The shaded region between 25 and 27 represents \(30\% \) of the distribution.
Find \({\rm{P}}(X > 27)\) .
Find the standard deviation of X .
Answer/Explanation
Markscheme
symmetry of normal curve (M1)
e.g. \({\rm{P}}(X < 25) = 0.5\)
\({\rm{P}}(X > 27) = 0.2\) A1 N2
[2 marks]
METHOD 1
finding standardized value (A1)
e.g. \(\frac{{27 – 25}}{\sigma }\)
evidence of complement (M1)
e.g. \(1 – p\) , \({\rm{P}}(X < 27)\) , 0.8
finding z-score (A1)
e.g. \(z = 0.84 \ldots \)
attempt to set up equation involving the standardized value M1
e.g. \(0.84 = \frac{{27 – 25}}{\sigma }\) , \(0.84 = \frac{{X – \mu }}{\sigma }\)
\(\sigma = 2.38\) A1 N3
METHOD 2
set up using normal CDF function and probability (M1)
e.g. \({\rm{P}}(25 < X < 27) = 0.3\) , \({\rm{P}}(X < 27) = 0.8\)
correct equation A2
e.g. \({\rm{P}}(25 < X < 27) = 0.3\) , \({\rm{P}}(X > 27) = 0.2\)
attempt to solve the equation using GDC (M1)
e.g. solver, graph, trial and error (more than two trials must be shown)
\(\sigma = 2.38\) A1 N3
[5 marks]
Question
A company produces a large number of water containers. Each container has two parts, a bottle and a cap. The bottles and caps are tested to check that they are not defective.
A cap has a probability of 0.012 of being defective. A random sample of 10 caps is selected for inspection.
Find the probability that exactly one cap in the sample will be defective.
The sample of caps passes inspection if at most one cap is defective. Find the probability that the sample passes inspection.
The heights of the bottles are normally distributed with a mean of \(22{\text{ cm}}\) and a standard deviation of \(0.3{\text{ cm}}\).
(i) Copy and complete the following diagram, shading the region representing where the heights are less than \(22.63{\text{ cm}}\).
(ii) Find the probability that the height of a bottle is less than \(22.63{\text{ cm}}\).
(i) A bottle is accepted if its height lies between \(21.37{\text{ cm}}\) and \(22.63{\text{ cm}}\). Find the probability that a bottle selected at random is accepted.
(ii) A sample of 10 bottles passes inspection if all of the bottles in the sample are accepted. Find the probability that the sample passes inspection.
The bottles and caps are manufactured separately. A sample of 10 bottles and a sample of 10 caps are randomly selected for testing. Find the probability that both samples pass inspection.
Answer/Explanation
Markscheme
Note: There may be slight differences in answers, depending on whether candidates use tables or GDCs, or their 3 sf answers in subsequent parts. Do not penalise answers that are consistent with their working and check carefully for FT.
evidence of recognizing binomial (seen anywhere in the question) (M1)
e.g. \(_n{C_r}{p^r}{q^{n – r}}\) , \({\text{B}}(n{\text{, }}p)\) , \(^{10}{C_1}{(0.012)^1}{(0.988)^9}\)
\(p = 0.108\) A1 N2
[2 marks]
valid approach (M1)
e.g. \({\rm{P}}(X \le 1)\) , \(0.88627 \ldots + 0.10764 \ldots \)
\(p = 0.994\) A1 N2
[2 marks]
(i)
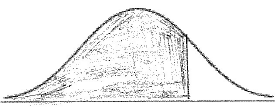A1A1 N2
Note: Award A1 for vertical line to right of mean, A1 for shading to left of their vertical line.
(ii) valid approach (M1)
e.g. \({\rm{P}}(X < 22.63)\)
working to find standardized value (A1)
e.g. \(\frac{{22.63 – 22}}{{0.3}}\) , 2.1
\(p = 0.982\) A1 N3
[5 marks]
valid approach (M1)
e.g. \({\rm{P}}(21.37 < X < 22.63)\) , \({\rm{P}}( – 2.1 < z < 2.1)\)
correct working (A1)
e.g. \(0.982 – (1 – 0.982)\)
\(p = 0.964\) A1 N3
(ii) correct working (A1)
e.g. \(X \sim {\rm{B}}(10,0.964)\) , \({(0.964)^{10}}\)
\(p = 0.695\) (accept 0.694 from tables) A1 N2
[5 marks]
valid approach (M1)
e.g. \({\rm{P}}(A \cap B) = {\rm{P}}(A){\rm{P}}(B)\) , \((0.994) \times {(0.964)^{10}}\)
\(p = 0.691\) (accept \(0.690\) from tables) A1 N2
[2 marks]
Question
In a large city, the time taken to travel to work is normally distributed with mean \(\mu \) and standard deviation \(\sigma \) . It is found that \(4\% \) of the population take less than 5 minutes to get to work, and \(70\% \) take less than 25 minutes.
Find the value of \(\mu \) and of \(\sigma \) .
Answer/Explanation
Markscheme
correct z-values (A1)(A1)
\( – 1.750686 \ldots \) , \(0.524400 \ldots \)
attempt to set up their equations, must involve z-values, not % (M1)
e.g. one correct equation
two correct equations A1A1
e.g. \(\mu – 1.750686\sigma = 5\) , \(0.5244005 = \frac{{25 – \mu }}{\sigma }\)
attempt to solve their equations (M1)
e.g. substitution, matrices, one correct value
\(\mu = 20.39006 \ldots \) , \(\sigma = 8.790874 \ldots \)
\(\mu = 20.4\) \([20.3{\text{, }}20.4]\), \(\sigma = 8.79\) \([8.79{\text{, }}8.80]\) A1A1 N4
[8 marks]
Question
A random variable \(X\) is normally distributed with \(\mu = 150\) and \(\sigma = 10\) .
Find the interquartile range of \(X\) .
Answer/Explanation
Markscheme
recognizing one quartile probability (may be seen in a sketch) (M1)
eg \({\rm{P}}(X < {Q_3}) = 0.75\) , \(0.25\)
finding standardized value for either quartile (A1)
eg \(z = 0.67448 \ldots \) , \(z = – 0.67448 \ldots \)
attempt to set up equation (must be with \(z\)-values) (M1)
eg \(0.67 = \frac{{{Q_3} – 150}}{{10}}\) , \( – 0.67448 = \frac{{x – 150}}{{10}}\)
one correct quartile
eg \({Q_3} = 156.74 \ldots \) , \({Q_1} = 143.25 \ldots \)
correct working (A1)
eg other correct quartile, \({Q_3} – \mu = 6.744 \ldots \)
valid approach for IQR (seen anywhere) (A1)
eg \({Q_3} – {Q_1}\) , \(2({Q_3} – \mu )\)
IQR \( = 13.5\) A1 N4
[7 marks]
Question
The random variable \(X\) is normally distributed with mean \(20\) and standard deviation \(5\).
Find \({\rm{P}}(X \le 22.9)\) .
Given that \({\rm{P}}(X < k) = 0.55\) , find the value of \(k\) .
Answer/Explanation
Markscheme
evidence of appropriate approach (M1)
eg \(z = \frac{{22.9 – 20}}{5}\)
\(z = 0.58\) (A1)
\({\rm{P}}(X \le 22.9) = 0.719\) A1 N3
[3 marks]
\(z\)-score for \(0.55\) is \(0.12566…\) (A1)
valid approach (must be with \(z\)-values) (M1)
eg using inverse normal, \(0.1257 = \frac{{k – 20}}{5}\)
\(k = 20.6\) A1 N3
[3 marks]
Question
The time taken for a student to complete a task is normally distributed with a mean of \(20\) minutes and a standard deviation of \(1.25\) minutes.
A student is selected at random. Find the probability that the student completes the task in less than \(21.8\) minutes.
The probability that a student takes between \(k\) and \(21.8\) minutes is \(0.3\). Find the value of \(k\).
Answer/Explanation
Markscheme
Note: There may be slight differences in answers, depending on whether candidates use tables or GDCs, or their 3 sf answers in subsequent parts. Do not penalise answers that are consistent with their working and check carefully for FT.
attempt to standardize (M1)
eg \(z = \frac{{21.8 – 20}}{{1.25}},{\text{ 1.44}}\)
\({\text{P}}(T < 21.8) = 0.925\) A1 N2
[2 marks]
Note: There may be slight differences in answers, depending on whether candidates use tables or GDCs, or their 3 sf answers in subsequent parts. Do not penalise answers that are consistent with their working and check carefully for FT.
attempt to subtract probabilities (M1)
eg \({\text{P}}(T < 21.8) – {\text{P}}(T < k) = 0.3,{\text{ }}0.925 – 0.3\)
\({\text{P}}(T < k) = 0.625\) A1
EITHER
finding the \(z\)-value for \(0.625\) (A1)
eg \(z = 0.3186\) (from tables), \(z = 0.3188\)
attempt to set up equation using their \(z\)-value (M1)
eg \(0.3186 = \frac{{k – 20}}{{1.25}},{\text{ }} – 0.524 \times 1.25 = k – 20\)
\(k = 20.4\) A1 N3
OR
\(k = 20.4\) A3 N3
[5 marks]
Question
A forest has a large number of tall trees. The heights of the trees are normally distributed with a mean of \(53\) metres and a standard deviation of \(8\) metres. Trees are classified as giant trees if they are more than \(60\) metres tall.
A tree is selected at random from the forest.
Find the probability that this tree is a giant.
A tree is selected at random from the forest.
Given that this tree is a giant, find the probability that it is taller than \(70\) metres.
Two trees are selected at random. Find the probability that they are both giants.
\(100\) trees are selected at random.
Find the expected number of these trees that are giants.
\(100\) trees are selected at random.
Find the probability that at least \(25\) of these trees are giants.
Answer/Explanation
Markscheme
valid approach (M1)
eg \({\text{P}}(G) = {\text{P}}(H > 60,{\text{ }}z = 0.875,{\text{ P}}(H > 60) = 1 – 0.809,{\text{ N}}\left( {53, {8^2}} \right)\)
\(0.190786\)
\({\text{P}}(G) = 0.191\) A1 N2
[3 marks]
finding \({\text{P}}(H > 70) = 0.01679\) (seen anywhere) (A1)
recognizing conditional probability (R1)
eg \({\text{P}}(A\left| {B),{\text{ P}}(H > 70\left| {H > 60)} \right.} \right.\)
correct working (A1)
eg \(\frac{{0.01679}}{{0.191}}\)
\(0.0880209\)
\({\text{P}}(X > 70\left| {G) = 0.0880} \right.\) A1 N3
[6 marks]
attempt to square their \({\text{P}}(G)\) (M1)
eg \({0.191^2}\)
\(0.0363996\)
\({\text{P}}({\text{both }}G) = 0.0364\) A1 N2
[2 marks]
correct substitution into formula for \({\text{E}}(X)\) (A1)
eg \(100(0.191)\)
\({\text{E}}(G) = 19.1{\text{ }}[19.0,{\text{ }}19.1]\) A1 N2
[3 marks]
recognizing binomial probability (may be seen in part (c)(i)) (R1)
eg \(X \sim {\text{B}}(n,{\text{ }}p)\)
valid approach (seen anywhere) (M1)
eg \({\text{P}}(X \geqslant 25) = 1 – {\text{P}}(X \leqslant 24),{\text{ }}1 – {\text{P}}(X < a)\)
correct working (A1)
eg \({\text{P}}(X \leqslant 24) = 0.913 \ldots ,{\text{ }}1 – 0.913 \ldots \)
\(0.0869002\)
\({\text{P}}(X \geqslant 25) = 0.0869\) A1 N2
[3 marks]
Question
The weights of fish in a lake are normally distributed with a mean of \(760\) g and standard deviation \(\sigma \). It is known that \(78.87\% \) of the fish have weights between \(705\) g and \(815\) g.
(i) Write down the probability that a fish weighs more than \(760\) g.
(ii) Find the probability that a fish weighs less than \(815\) g.
(i) Write down the standardized value for \(815\) g.
(ii) Hence or otherwise, find \(\sigma \).
A fishing contest takes place in the lake. Small fish, called tiddlers, are thrown back into the lake. The maximum weight of a tiddler is \(1.5\) standard deviations below the mean.
Find the maximum weight of a tiddler.
A fish is caught at random. Find the probability that it is a tiddler.
\(25\% \) of the fish in the lake are salmon. \(10\% \) of the salmon are tiddlers. Given that a fish caught at random is a tiddler, find the probability that it is a salmon.
Answer/Explanation
Markscheme
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
(i) \({\text{P}}(X > 760) = 0.5{\text{ (exact), }}[0.499,{\text{ }}0.500]{\text{ }}\) A1 N1
(ii) evidence of valid approach (M1)
recognising symmetry, \(\frac{{0.7887}}{2},{\text{ }}1 – {\text{P}}(W < 815),{\text{ }}\frac{{21.13}}{2} + 78.87\% \)
correct working (A1)
eg\(\;\;\;\)\(0.5 + 0.39435,{\text{ }}1 – 0.10565,\)
\(0.89435{\text{ (exact)}},{\text{ }}0.894{\text{ }}[0.894,{\text{ }}0.895]\) A1 N2
[4 marks]
(i) \(1.24999\) A1 N1
\(z = 1.25{\text{ }}[1.24,{\text{ }}1.25]\)
(ii) evidence of appropriate approach (M1)
eg\(\;\;\;\)\(\sigma = \frac{{x – \mu }}{{1.25}},{\text{ }}\frac{{815 – 760}}{\sigma }\)
correct substitution (A1)
eg\(\;\;\;\)\(1.25 = \frac{{815 – 760}}{\sigma },{\text{ }}\frac{{815 – 760}}{{1.24999}}\)
\(44.0003\)
\(\sigma = 44.0{\text{ }}[44.0,{\text{ }}44.1]{\text{ (g)}}\) A1 N2
[4 marks]
correct working (A1)
eg\(\;\;\;\)\(760 – 1.5 \times 44\)
\(693.999\)
\(694{\text{ }}[693,{\text{ }}694]{\text{ (g)}}\) A1 N2
[2 marks]
\(0.0668056\)
\({\text{P}}(X < 694) = 0.0668{\text{ }}[0.0668,{\text{ }}0.0669]\) A2 N2
[2 marks]
recognizing conditional probability (seen anywhere) (M1)
eg\(\;\;\;\)\({\text{P}}({\text{A}}|{\text{B}}),{\text{ }}\frac{{0.025}}{{0.0668}}\)
appropriate approach involving conditional probability (M1)
eg\(\;\;\;\)\({\text{P}}(S|T) = \frac{{{\text{P}}(S{\text{ and }}T)}}{{{\text{P}}(T)}}\),
correct working
eg\(\;\;\;\)P (salmon and tiddler) \( = 0.25 \times 0.1,{\text{ }}\frac{{0.25 \times 0.1}}{{0.0668}}\) (A1)
\(0.374220\)
\(0.374{\text{ }}[0.374,{\text{ }}0.375]\) A1 N2
[4 marks]
Total [16 marks]
Question
A company makes containers of yogurt. The volume of yogurt in the containers is normally distributed with a mean of \(260\) ml and standard deviation of \(6\) ml.
A container which contains less than \(250\) ml of yogurt is underfilled.
A container is chosen at random. Find the probability that it is underfilled.
The company decides that the probability of a container being underfilled should be reduced to \(0.02\). It decreases the standard deviation to \(\sigma \) and leaves the mean unchanged.
Find \(\sigma \).
The company changes to the new standard deviation, \(\sigma \), and leaves the mean unchanged.
A container is chosen at random for inspection. It passes inspection if its volume of yogurt is between \(250\) and \(271\) ml.
(i) Find the probability that it passes inspection.
(ii) Given that the container is not underfilled, find the probability that it passes inspection.
A sample of \(50\) containers is chosen at random. Find the probability that \(48\) or more of the containers pass inspection.
Answer/Explanation
Markscheme
\(0.0477903\)
probability \( = 0.0478\) A2 N2
[2 marks]
\({\text{P}}({\text{volume}} < 250) = 0.02\) (M1)
\(z = – 2.05374\;\;\;\)(may be seen in equation) A1
attempt to set up equation with \(z\) (M1)
eg\(\;\;\;\frac{{\mu – 260}}{\sigma } = z,{\text{ }}260 – 2.05(\sigma ) = 250\)
\(4.86914\)
\(\sigma = 4.87{\text{ (ml)}}\) A1 N3
[4 marks]
(i) \(0.968062\)
\({\text{P}}(250 < {\text{Vol}} < 271) = 0.968\) A2 N2
(ii) recognizing conditional probability (seen anywhere, including in correct working) R1
eg\(\;\;\;{\text{P}}(A|B),{\text{ }}\frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}},{\text{ P}}(A \cap B) = {\text{P}}(A|B){\text{P}}(B)\)
correct value or expression for \(P\) (not underfilled) (A1)
eg\(\;\;\;0.98,1 – 0.02,{\text{ }}1 – {\text{P}}(X < 250)\)
probability \( = \frac{{0.968}}{{0.98}}\) A1
\(0.987818\)
probability \( = 0.988\) A1 N2
[6 marks]
METHOD 1
evidence of recognizing binomial distribution (seen anywhere) (M1)
eg\(\;\;\;X\;\;\;{\text{B}}(50,{\text{ }}0.968),{\text{ binomial cdf, }}p = 0.968,{\text{ }}r = 47\)
\({\text{P}}(X \le 47\)) = 0.214106\) (A1)
evidence of using complement (M1)
eg\(\;\;\;1 – {\text{P}}(X \le 47\))
\(0.785894\)
probability \( = 0.786\) A1 N3
METHOD 2
evidence of recognizing binomial distribution (seen anywhere) (M1)
eg\(\;\;\;X\;\;\;{\text{B}}(50,{\text{ }}0.968),{\text{ binomial cdf, }}p = 0.968,{\text{ }}r = 47\)
\({\text{P(not pass)}} = 1 – {\text{P(pass)}} = 0.0319378\) (A1)
evidence of attempt to find \(P\) (\(2\) or fewer fail) (M1)
eg\(\;\;\;\)\(0\), \(1\), or \(2\) not pass, \({\text{B}}(50,{\text{ }}2)\)
\(0.785894\)
probability \( = 0.786\) A1 N3
METHOD 3
evidence of recognizing binomial distribution (seen anywhere) (M1)
eg\(\;\;\;X\;\;\;{\text{B}}(50,{\text{ }}0.968),{\text{ binomial cdf, }}p = 0.968,{\text{ }}r = 47\)
evidence of summing probabilities (M1)
eg\(\;\;\;{\text{P}}(X = 48) + {\text{P}}(X = 49) + {\text{P}}(X = 50)\)
correct working
eg\(\;\;\;0.263088 + 0.325488 + 0.197317\) (A1)
\(0.785894\)
probability \( = 0.786\) A1 N3
[4 marks]
Total [16 marks]
Question
The masses of watermelons grown on a farm are normally distributed with a mean of \(10\) kg.
The watermelons are classified as small, medium or large.
A watermelon is small if its mass is less than \(4\) kg. Five percent of the watermelons are classified as small.
Find the standard deviation of the masses of the watermelons.
The following table shows the percentages of small, medium and large watermelons grown on the farm.
A watermelon is large if its mass is greater than \(w\) kg.
Find the value of \(w\).
All the medium and large watermelons are delivered to a grocer.
The grocer selects a watermelon at random from this delivery. Find the probability that it is medium.
All the medium and large watermelons are delivered to a grocer.
The grocer sells all the medium watermelons for $1.75 each, and all the large watermelons for $3.00 each. His costs on this delivery are $300, and his total profit is $150. Find the number of watermelons in the delivery.
Answer/Explanation
Markscheme
finding standardized value for 4 kg (seen anywhere) (A1)
eg\(\;\;\;z = – 1.64485\)
attempt to standardize (M1)
eg\(\;\;\;\sigma = \frac{{x – \mu }}{z},{\text{ }}\frac{{4 – 10}}{\sigma }\)
correct substitution (A1)
eg\(\;\;\; – 1.64 = \frac{{4 – 10}}{\sigma },{\text{ }}\frac{{4 – 10}}{{ – 1.64}}\)
\(\sigma = 3.64774\)
\(\sigma = 3.65\) A1 N2
[4 marks]
valid approach (M1)
eg\(\;\;\;1 – p,{\text{ 0.62, }}\frac{{w – 10}}{{3.65}} = 0.305\)
\(w = 11.1143\)
\(w = 11.1\) A1 N2
[2 marks]
attempt to restrict melon population (M1)
eg\(\;\;\;\)\(95\% \) are delivered, \({\text{P}}({\text{medium}}|{\text{delivered}}),{\text{ }}57 + 38\)
correct probability for medium watermelons (A1)
eg\(\;\;\;\frac{{0.57}}{{0.95}}\)
\(\frac{{57}}{{95}},{\text{ }}0.6,{\text{ }}60\% \) A1 N3
[3 marks]
proportion of large watermelons (seen anywhere) (A1)
eg\(\;\;\;{\text{P(large)}} = 0.4,{\text{ }}40\% \)
correct approach to find total sales (seen anywhere) (A1)
eg\(\;\;\;150 = {\text{sales}} – 300,{\text{ total sales}} = \$ 450\)
correct expression (A1)
eg\(\;\;\;1.75(0.6x) + 3(0.4x),{\text{ }}1.75(0.6) + 3(0.4)\)
evidence of correct working (A1)
eg\(\;\;\;1.75(0.6x) + 3(0.4x) = 450,{\text{ }}2.25x = 450\)
200 watermelons in the delivery A1 N2
Notes: If candidate answers 0.57 in part (c), the FT values are \({\text{P(large)}} = 0.43\) and 197 watermelons. Award FT marks if working shown.
Award N0 for 197.
Question
A random variable \(X\) is distributed normally with a mean of 20 and standard deviation of 4.
On the following diagram, shade the region representing \({\text{P}}(X \leqslant 25)\).
Write down \({\text{P}}(X \leqslant 25)\), correct to two decimal places.
Let \({\text{P}}(X \leqslant c) = 0.7\). Write down the value of \(c\).
Answer/Explanation
Markscheme
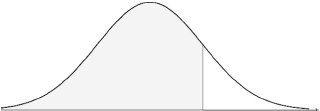A1A1 N2
Note: Award A1 for vertical line clearly to right of mean,
A1 for shading to left of their vertical line.
\({\text{P}}(X \leqslant 25) = 0.894350\) (A1)
\({\text{P}}(X \leqslant 25) = 0.89\) (must be 2 d.p.) A1 N2
[2 marks]
\(c = 22.0976\)
\(c = 22.1\) A2 N2
[2 marks]
Question
A competition consists of two independent events, shooting at 100 targets and running for one hour.
The number of targets a contestant hits is the \(S\) score. The \(S\) scores are normally distributed with mean 65 and standard deviation 10.
The distance in km that a contestant runs in one hour is the \(R\) score. The \(R\) scores are normally distributed with mean 12 and standard deviation 2.5. The \(R\) score is independent of the \(S\) score.
Contestants are disqualified if their \(S\) score is less than 50 and their \(R\) score is less than \(x\) km.
A contestant is chosen at random. Find the probability that their \(S\) score is less than 50.
Given that 1% of the contestants are disqualified, find the value of \(x\).
Answer/Explanation
Markscheme
0.0668072
\({\text{P}}(S < 50) = 0.0668{\text{ }}({\text{accept P}}(S \leqslant 49) = 0.0548)\) A2 N2
[2 marks]
valid approach (M1)
Eg\(\,\,\,\,\,\)\({\text{P}}(S < 50) \times {\text{P}}(R < x)\)
correct equation (accept any variable) A1
eg\(\,\,\,\,\,\)\({\text{P}}(S < 50) \times {\text{P}}(R < x) = 1\% ,{\text{ }}0.0668072 \times p = 0.01,{\text{ P}}(R < x) = \frac{{0.01}}{{0.0668}}\)
finding the value of \({\text{P}}(R < x)\) (A1)
eg\(\,\,\,\,\,\)\(\frac{{0.01}}{{0.0668}},{\text{ }}0.149684\)
9.40553
\(x = 9.41{\text{ }}({\text{accept }}x = 9.74{\text{ from }}0.0548)\) A1 N3
[4 marks]
Question
The heights of adult males in a country are normally distributed with a mean of 180 cm and a standard deviation of \(\sigma {\text{ cm}}\). 17% of these men are shorter than 168 cm. 80% of them have heights between \((192 – h){\text{ cm}}\) and 192 cm.
Find the value of \(h\).
Answer/Explanation
Markscheme
finding the \(z\)-value for 0.17 (A1)
eg\(\,\,\,\,\,\)\(z = – 0.95416\)
setting up equation to find \(\sigma \), (M1)
eg\(\,\,\,\,\,\)\(z = \frac{{168 – 180}}{\sigma },{\text{ }} – 0.954 = \frac{{ – 12}}{\sigma }\)
\(\sigma = 12.5765\) (A1)
EITHER (Properties of the Normal curve)
correct value (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\({\text{P}}(X < 192) = 0.83,{\text{ P}}(X > 192) = 0.17\)
correct working (A1)
eg\(\,\,\,\,\,\)\({\text{P}}(X < 192 – h) = 0.83 – 0.8,{\text{ P}}(X < 192 – h) = 1 – 0.8 – 0.17,\)
\({\text{P}}(X > 192 – h) = 0.8 + 0.17\)
correct equation in \(h\)
eg\(\,\,\,\,\,\)\(\frac{{(192 – h) – 180}}{{12.576}} = – 1.88079,{\text{ }}192 – h = 156.346\) (A1)
35.6536
\(h = 35.7\) A1 N3
OR (Trial and error using different values of h)
two correct probabilities whose 2 sf will round up and down, respectively, to 0.8 A2
eg\(\,\,\,\,\,\)\({\text{P}}(192 – 35.6 < X < 192) = 0.799706,{\text{ P}}(157 < X < 192) = 0.796284,\)
\({\text{P}}(192 – 36 < X < 192) = 0.801824\)
\(h = 35.7\) A2
[7 marks]
Question
The mass M of apples in grams is normally distributed with mean μ. The following table shows probabilities for values of M.
The apples are packed in bags of ten.
Any apples with a mass less than 95 g are classified as small.
Write down the value of k.
Show that μ = 106.
Find P(M < 95) .
Find the probability that a bag of apples selected at random contains at most one small apple.
Find the expected number of bags in this crate that contain at most one small apple.
Find the probability that at least 48 bags in this crate contain at most one small apple.
Answer/Explanation
Markscheme
evidence of using \(\sum {{p_i}} = 1\) (M1)
eg k + 0.98 + 0.01 = 1
k = 0.01 A1 N2
[2 marks]
recognizing that 93 and 119 are symmetrical about μ (M1)
eg μ is midpoint of 93 and 119
correct working to find μ A1
\(\frac{{119 + 93}}{2}\)
μ = 106 AG N0
[2 marks]
finding standardized value for 93 or 119 (A1)
eg z = −2.32634, z = 2.32634
correct substitution using their z value (A1)
eg \(\frac{{93 – 106}}{\sigma } = – 2.32634,\,\,\frac{{119 – 106}}{{2.32634}} = \sigma \)
σ = 5.58815 (A1)
0.024508
P(X < 95) = 0.0245 A2 N3
[5 marks]
evidence of recognizing binomial (M1)
eg 10, ananaCpqn−=××and 0.024B(5,,)pnp=
valid approach (M1)
eg P(1),P(0)P(1)XXX≤=+=
0.976285
0.976 A1 N2
[3 marks]
recognizing new binomial probability (M1)
eg B(50, 0.976)
correct substitution (A1)
eg E(X) = 50 (0.976285)
48.81425
48.8 A1 N2
[3 marks]
valid approach (M1)
eg P(X ≥ 48), 1 − P(X ≤ 47)
0.884688
0.885 A1 N2
[2 marks]
Question
A random variable X is distributed normally with mean 450. It is known that \({\rm{P}}(X > a) = 0.27\) .
Represent all this information on the following diagram.
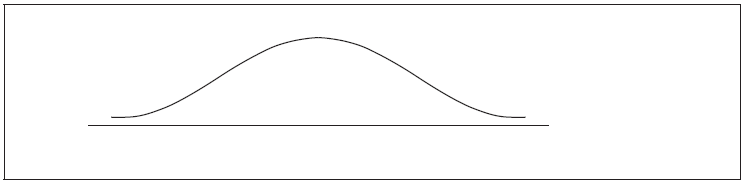
Given that the standard deviation is 20, find a . Give your answer correct to the nearest whole number.
Answer/Explanation
Markscheme
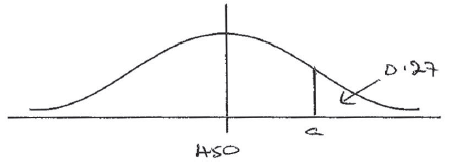A1A1A1 N3
Note: Award A1 for 450 , A1 for a to the right of the mean, A1 for area 0.27 .
[3 marks]
valid approach M1
e.g. \({\rm{P}}(X < a) = 1 – {\rm{P}}(X > a)\) , 0.73
\(a = 462.256 \ldots \) A1
\(a = 462\) A1 N3
[3 marks]