Question
Let \(f(x) = \frac{1}{{x – 1}} + 2\), for \(x > 1\).
Let \(g(x) = a{e^{ – x}} + b\), for \(x \geqslant 1\). The graphs of \(f\) and \(g\) have the same horizontal asymptote.
Write down the equation of the horizontal asymptote of the graph of \(f\).
Find \(f'(x)\).
Write down the value of \(b\).
Given that \(g'(1) = – e\), find the value of \(a\).
There is a value of \(x\), for \(1 < x < 4\), for which the graphs of \(f\) and \(g\) have the same gradient. Find this gradient.
Answer/Explanation
Markscheme
\(y = 2\) (correct equation only) A2 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\({(x – 1)^{ – 1}} + 2,{\text{ }}f'(x) = \frac{{0(x – 1) – 1}}{{{{(x – 1)}^2}}}\)
\( – {(x – 1)^{ – 2}},{\text{ }}f'(x) = \frac{{ – 1}}{{{{(x – 1)}^2}}}\) A1 N2
[2 marks]
correct equation for the asymptote of \(g\)
eg\(\,\,\,\,\,\)\(y = b\) (A1)
\(b = 2\) A1 N2
[2 marks]
correct derivative of g (seen anywhere) (A2)
eg\(\,\,\,\,\,\)\(g'(x) = – a{{\text{e}}^{ – x}}\)
correct equation (A1)
eg\(\,\,\,\,\,\)\( – {\text{e}} = – a{{\text{e}}^{ – 1}}\)
7.38905
\(a = {{\text{e}}^2}{\text{ }}({\text{exact}}),{\text{ }}7.39\) A1 N2
[4 marks]
attempt to equate their derivatives (M1)
eg\(\,\,\,\,\,\)\(f'(x) = g'(x),{\text{ }}\frac{{ – 1}}{{{{(x – 1)}^2}}} = – a{{\text{e}}^{ – x}}\)
valid attempt to solve their equation (M1)
eg\(\,\,\,\,\,\)correct value outside the domain of \(f\) such as 0.522 or 4.51,
correct solution (may be seen in sketch) (A1)
eg\(\,\,\,\,\,\)\(x = 2,{\text{ }}(2,{\text{ }} – 1)\)
gradient is \( – 1\) A1 N3
[4 marks]
Question
The following diagram shows the graph of \(f(x) = a\sin bx + c\), for \(0 \leqslant x \leqslant 12\).
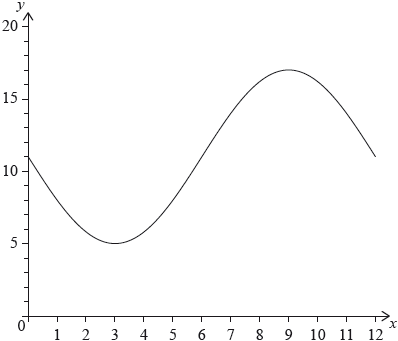
The graph of \(f\) has a minimum point at \((3,{\text{ }}5)\) and a maximum point at \((9,{\text{ }}17)\).
The graph of \(g\) is obtained from the graph of \(f\) by a translation of \(\left( {\begin{array}{*{20}{c}} k \\ 0 \end{array}} \right)\). The maximum point on the graph of \(g\) has coordinates \((11.5,{\text{ }}17)\).
The graph of \(g\) changes from concave-up to concave-down when \(x = w\).
(i) Find the value of \(c\).
(ii) Show that \(b = \frac{\pi }{6}\).
(iii) Find the value of \(a\).
(i) Write down the value of \(k\).
(ii) Find \(g(x)\).
(i) Find \(w\).
(ii) Hence or otherwise, find the maximum positive rate of change of \(g\).
Answer/Explanation
Markscheme
(i) valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{5 + 17}}{2}\)
\(c = 11\) A1 N2
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)period is 12, per \( = \frac{{2\pi }}{b},{\text{ }}9 – 3\)
\(b = \frac{{2\pi }}{{12}}\) A1
\(b = \frac{\pi }{6}\) AG N0
(iii) METHOD 1
valid approach (M1)
eg\(\,\,\,\,\,\)\(5 = a\sin \left( {\frac{\pi }{6} \times 3} \right) + 11\), substitution of points
\(a = – 6\) A1 N2
METHOD 2
valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{17 – 5}}{2}\), amplitude is 6
\(a = – 6\) A1 N2
[6 marks]
(i) \(k = 2.5\) A1 N1
(ii) \(g(x) = – 6\sin \left( {\frac{\pi }{6}(x – 2.5)} \right) + 11\) A2 N2
[3 marks]
(i) METHOD 1 Using \(g\)
recognizing that a point of inflexion is required M1
eg\(\,\,\,\,\,\)sketch, recognizing change in concavity
evidence of valid approach (M1)
eg\(\,\,\,\,\,\)\(g”(x) = 0\), sketch, coordinates of max/min on \({g’}\)
\(w = 8.5\) (exact) A1 N2
METHOD 2 Using \(f\)
recognizing that a point of inflexion is required M1
eg\(\,\,\,\,\,\)sketch, recognizing change in concavity
evidence of valid approach involving translation (M1)
eg\(\,\,\,\,\,\)\(x = w – k\), sketch, \(6 + 2.5\)
\(w = 8.5\) (exact) A1 N2
(ii) valid approach involving the derivative of \(g\) or \(f\) (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(g'(w),{\text{ }} – \pi \cos \left( {\frac{\pi }{6}x} \right)\), max on derivative, sketch of derivative
attempt to find max value on derivative M1
eg\(\,\,\,\,\,\)\( – \pi \cos \left( {\frac{\pi }{6}(8.5 – 2.5)} \right),{\text{ }}f'(6)\), dot on max of sketch
3.14159
max rate of change \( = \pi \) (exact), 3.14 A1 N2
[6 marks]
Question
Let \(f(x) = – 0.5{x^4} + 3{x^2} + 2x\). The following diagram shows part of the graph of \(f\).
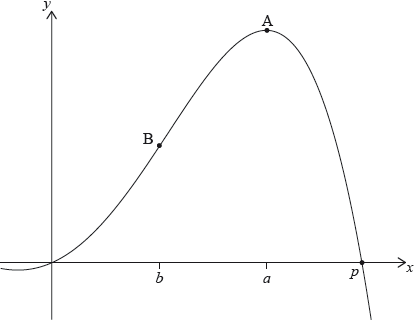
There are \(x\)-intercepts at \(x = 0\) and at \(x = p\). There is a maximum at A where \(x = a\), and a point of inflexion at B where \(x = b\).
Find the value of \(p\).
Write down the coordinates of A.
Write down the rate of change of \(f\) at A.
Find the coordinates of B.
Find the the rate of change of \(f\) at B.
Let \(R\) be the region enclosed by the graph of \(f\) , the \(x\)-axis, the line \(x = b\) and the line \(x = a\). The region \(R\) is rotated 360° about the \(x\)-axis. Find the volume of the solid formed.
Answer/Explanation
Markscheme
evidence of valid approach (M1)
eg\(\,\,\,\,\,\)\(f(x) = 0,{\text{ }}y = 0\)
2.73205
\(p = 2.73\) A1 N2
[2 marks]
1.87938, 8.11721
\((1.88,{\text{ }}8.12)\) A2 N2
[2 marks]
rate of change is 0 (do not accept decimals) A1 N1
[1 marks]
METHOD 1 (using GDC)
valid approach M1
eg\(\,\,\,\,\,\)\(f’’ = 0\), max/min on \(f’,{\text{ }}x = – 1\)
sketch of either \(f’\) or \(f’’\), with max/min or root (respectively) (A1)
\(x = 1\) A1 N1
Substituting their \(x\) value into \(f\) (M1)
eg\(\,\,\,\,\,\)\(f(1)\)
\(y = 4.5\) A1 N1
METHOD 2 (analytical)
\(f’’ = – 6{x^2} + 6\) A1
setting \(f’’ = 0\) (M1)
\(x = 1\) A1 N1
substituting their \(x\) value into \(f\) (M1)
eg\(\,\,\,\,\,\)\(f(1)\)
\(y = 4.5\) A1 N1
[4 marks]
recognizing rate of change is \(f’\) (M1)
eg\(\,\,\,\,\,\)\(y’,{\text{ }}f’(1)\)
rate of change is 6 A1 N2
[3 marks]
attempt to substitute either limits or the function into formula (M1)
involving \({f^2}\) (accept absence of \(\pi \) and/or \({\text{d}}x\))
eg\(\,\,\,\,\,\)\(\pi \int {{{( – 0.5{x^4} + 3{x^2} + 2x)}^2}{\text{d}}x,{\text{ }}\int_1^{1.88} {{f^2}} } \)
128.890
\({\text{volume}} = 129\) A2 N3
[3 marks]

