Question
Consider the graphs \(y = {{\text{e}}^{ – x}}\) and \(y = {{\text{e}}^{ – x}}\sin 4x\) , for \(0 \leqslant x \leqslant \frac{{5\pi }}{4}\) .
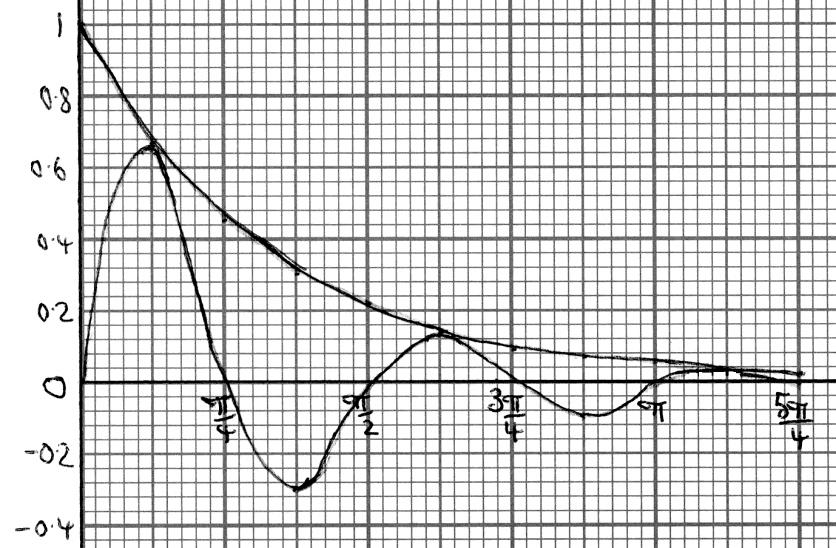
(a) On the same set of axes draw, on graph paper, the graphs, for \(0 \leqslant x \leqslant \frac{{5\pi }}{4}\). Use a scale of \(1\) cm to \(\frac{\pi }{8}\) on your \(x\)-axis and \(5\) cm to \(1\) unit on your \(y\)-axis.
(b) Show that the \(x\)-intercepts of the graph \(y = {{\text{e}}^{ – x}}\) sin 4x are \(\frac{{n\pi }}{4}\) , \(n = 0\), \(1\), \(2\), \(3\), \(4\), \(5\).
(c) Find the \(x\)-coordinates of the points at which the graph of \(y = {{\text{e}}^{ – x}}\sin 4x\) meets the graph of \(y = {{\text{e}}^{ – x}}\) . Give your answers in terms of \( \pi\).
(d) (i) Show that when the graph of \(y = {{\text{e}}^{ – x}}\sin 4x\) meets the graph of \(y = {{\text{e}}^{ – x}}\) , their gradients are equal.
(ii) Hence explain why these three meeting points are not local maxima of the graph \(y = {{\text{e}}^{ – x}}\sin 4x\) .
(e) (i) Determine the \(y\)-coordinates, \({y_1}\) , \({y_2}\) and \({y_3}\), where \({y_1} > {y_2} > {y_3}\) , of the local maxima of \(y = {{\text{e}}^{ – x}}\sin 4x\) for \(0 \leqslant x \leqslant \frac{{5\pi }}{4}\) . You do not need to show that they are maximum values, but the values should be simplified.
(ii) Show that \({y_1}\) , \({y_2}\) and \({y_3}\) form a geometric sequence and determine the common ratio \(r\)
▶️Answer/Explanation
Markscheme
(a)
 A3
A3
Note: Award A1 for each correct shape,
A1 for correct relative position.
[3 marks]
(b) \({{\text{e}}^{ – x}}\sin \left( {4x} \right) = 0\) (M1)
\(\sin \left( {4x} \right) = 0\) A1
\(4x = 0\), \(\pi \), \(2\pi \), \(3\pi \), \(4\pi \), \(5\pi \) A1
\(x = 0\), \(\frac{\pi }{4}\), \(\frac{2\pi }{4}\), \(\frac{3\pi }{4}\), \(\frac{4\pi }{4}\), \(\frac{5\pi }{4}\) AG
[3 marks]
(c) \({{\text{e}}^{ – x}} = {{\text{e}}^{ – x}}\sin \left( {4x} \right) = 0\) or reference to graph
\(\sin 4x = 1\), M1
\(\sin 4x = 1\), \(frac{\pi }{2}\), \(frac{5\pi }{2}\), \(frac{9\pi }{2}\) A1
\(x = \frac{\pi }{8}\), \(\frac{5\pi }{8}\), \(\frac{9\pi }{8}\) A1 N3[3 marks](d) (i) \(y = {{\text{e}}^{ – x}}\sin 4x\)\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – {{\text{e}}^{ – x}}\sin 4x + 4{{\text{e}}^{ – x}}\cos 4x\) M1A1\(y = {{\text{e}}^{ – x}}\)\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – {{\text{e}}^{ – x}}\) A1verifying equality of gradients at one point R1verifying at the other two R1(ii) since \(\frac{{{\text{d}}y}}{{{\text{d}}x}} \ne 0\) at these points they cannot be local maxima R1[6 marks](e) (i) maximum when \(y’ = 4{{\text{e}}^{ – x}}\cos 4x – {{\text{e}}^{ – x}}\sin 4x = 0\) M1\(x = \frac{{\arctan \left( 4 \right)}}{4}\), \(\frac{{\arctan \left( 4 \right) + \pi }}{4}\), \(\frac{{\arctan \left( 4 \right) + 2\pi }}{4}\), …maxima occur at\(x = \frac{{\arctan \left( 4 \right)}}{4}\), \(\frac{{\arctan \left( 4 \right) + 2\pi }}{4}\), \(\frac{{\arctan \left( 4 \right) + 4\pi }}{4}\) A1so \({y_1} = {{\text{e}}^{ – \frac{1}{4}\left( {\arctan \left( 4 \right)} \right)}}\sin \left( {\arctan \left( 4 \right)} \right)\) (\( = 0.696\)) A1\({y_2} = {{\text{e}}^{ – \frac{1}{4}\left( {\arctan \left( 4 \right) + 2\pi } \right)}}\sin \left( {\arctan \left( 4 \right) + 2\pi } \right)\) A1\(\left( { = {{\text{e}}^{ – \frac{1}{4}\left( {\arctan \left( 4 \right) + 2\pi } \right)}}\sin \left( {\arctan \left( 4 \right)} \right) = 0.145} \right)\)\({y_3} = {{\text{e}}^{ – \frac{1}{4}\left( {\arctan \left( 4 \right) + 4\pi } \right)}}\sin \left( {\arctan \left( 4 \right) + 4\pi } \right)\) A1\(\left( { = {{\text{e}}^{ – \frac{1}{4}\left( {\arctan \left( 4 \right) + 4\pi } \right)}}\sin \left( {\arctan \left( 4 \right)} \right) = 0.0301} \right)\) N3(ii) for finding and comparing \(\frac{{{y_3}}}{{{y_2}}}\) and \(\frac{{{y_2}}}{{{y_1}}}\) M1\(r = {{\text{e}}^{ – \frac{\pi }{2}}}\) A1Note: Exact values must be used to gain the M1 and the A1.[7 marks]Total [22 marks]Examiners report
Although the final question on the paper it had parts accessible even to the weakest candidates. The vast majority of candidates earned marks on part (a), although some graphs were rather scruffy. Many candidates also tackled parts (b), (c) and (d). In part (b), however, as the answer was given, it should have been clear that some working was required rather than reference to a graph, which often had no scale indicated. In part d(i), although the functions were usually differentiated correctly, it was often the case that only one point was checked for the equality of the gradients. In part e(i) many candidates who got this far were able to determine the \(y\)-coordinates of the local maxima numerically using a GDC, and that was given credit. Only the exact values, however, could be used in part e(ii).
Question
Consider the function \(f\) , defined by \(f(x) = x – a\sqrt x \) , where \(x \geqslant 0\), \(a \in {\mathbb{R}^ + }\) .
(a) Find in terms of \(a\)
(i) the zeros of \(f\) ;
(ii) the values of \(x\) for which \(f\) is decreasing;
(iii) the values of \(x\) for which \(f\) is increasing;
(iv) the range of \(f\) .
(b) State the concavity of the graph of \(f\) .
▶️Answer/Explanation
Markscheme
(a)
(i) \(x – a\sqrt x \) M1
\(\sqrt x \sqrt x – a = 0\) (A1)
2 \(x = 0\), \(x = {a^2}\) A1 N2
(ii) \(f'(x) = 1 – \frac{a}{{2\sqrt x }}\) A1
\(f\) is decreasing when \(f’ < 0\) (M1)
\(1 – \frac{a}{{2\sqrt x }} < 0 \Rightarrow \frac{{2\sqrt x – a}}{{2\sqrt x }} < 0 \Rightarrow x > \frac{{{a^2}}}{4}\) A1
(iii) \(f\) is increasing when \(f’ > 0\)
\(1 – \frac{a}{{2\sqrt x }} > 0 \Rightarrow \frac{{2\sqrt x – a}}{{2\sqrt x }} > 0 \Rightarrow x > \frac{{{a^2}}}{4}\) A1
Note: Award the M1 mark for either (ii) or (iii).
(iv) minimum occurs at \(x = \frac{{{a^2}}}{4}\)
minimum value is \(y = – \frac{{{a^2}}}{4}\) (M1)A1
hence \(y \geqslant – \frac{{{a^2}}}{4}\) A1
[10 marks]
(b) concave up for all values of \(x\) R1
[1 mark]
Total [11 marks]
Examiners report
This was generally a well answered question.
Question
The function f is defined on the domain [0, 2] by \(f(x) = \ln (x + 1)\sin (\pi x)\) .
a.Obtain an expression for \(f'(x)\) .[3]
b.Sketch the graphs of f and \(f’\) on the same axes, showing clearly all x-intercepts.[4]
c.Find the x-coordinates of the two points of inflexion on the graph of f .[2]
d.Find the equation of the normal to the graph of f where x = 0.75 , giving your answer in the form y = mx + c .[3]
e.Consider the points \({\text{A}}\left( {a{\text{ }},{\text{ }}f(a)} \right)\) , \({\text{B}}\left( {b{\text{ }},{\text{ }}f(b)} \right)\) and \({\text{C}}\left( {c{\text{ }},{\text{ }}f(c)} \right)\) where a , b and c \((a < b < c)\) are the solutions of the equation \(f(x) = f'(x)\) . Find the area of the triangle ABC.[6]
▶️Answer/Explanation
Markscheme
\(f'(x) = \frac{1}{{x + 1}}\sin (\pi x) + \pi \ln (x + 1)\cos (\pi x)\) M1A1A1
[3 marks]
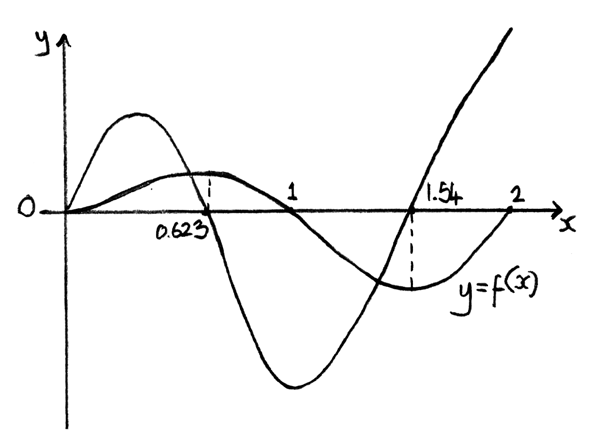 A4
A4
Note: Award A1A1 for graphs, A1A1 for intercepts.
[4 marks]
0.310, 1.12 A1A1
[2 marks]
\(f'(0.75) = – 0.839092\) A1
so equation of normal is \(y – 0.39570812 = \frac{1}{{0.839092}}(x – 0.75)\) M1
\(y = 1.19x – 0.498\) A1
[3 marks]
\({\text{A}}(0,{\text{ }}0)\)
\({\text{B(}}\overbrace {0.548 \ldots }^c,\overbrace {0.432 \ldots }^d)\) A1
\({\text{C(}}\overbrace {1.44 \ldots }^e,\overbrace { – 0.881 \ldots }^f)\) A1
Note: Accept coordinates for B and C rounded to 3 significant figures.
area \(\Delta {\text{ABC}} = \frac{1}{2}|\)(ci + dj) \( \times \) (ei + fj)\(|\) M1A1
\( = \frac{1}{2}(de – cf)\) A1
\( = 0.554\) A1
[6 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
