Question
The diagram below shows part of the graph of the gradient function, \(y = f'(x)\) .
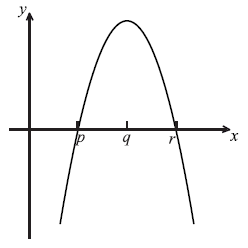
On the grid below, sketch a graph of \(y = f”(x)\) , clearly indicating the x-intercept.

Complete the table, for the graph of \(y = f(x)\) .

Justify your answer to part (b) (ii).
Answer/Explanation
Markscheme
 A1A1 N2
A1A1 N2
Note: Award A1 for negative gradient throughout, A1 for x-intercept of q. It need not be linear.
[2 marks]
A1A1 N1N1
METHOD 1
Second derivative is zero, second derivative changes sign. R1R1 N2
METHOD 2
There is a maximum on the graph of the first derivative. R2 N2
Examiners report
Several candidates had a correct sketch in part (a).
The majority of the errors occurred in parts (b) and (c). In part (b), some seemed to just guess while others left it blank.
In part (c), justification lacked completeness. For example, many stated that the second derivative must equal zero but said nothing of its change in sign.
Question
Let \(f'(x) = – 24{x^3} + 9{x^2} + 3x + 1\) .
There are two points of inflexion on the graph of f . Write down the x-coordinates of these points.
Let \(g(x) = f”(x)\) . Explain why the graph of g has no points of inflexion.
Answer/Explanation
Markscheme
valid approach R1
e.g. \(f”(x) = 0\) , the max and min of \(f’\) gives the points of inflexion on f
\( – 0.114{\text{, }}0.364\) (accept (\( – 0.114{\text{, }}0.811\)) and (\(0.364{\text{, }}2.13)\)) A1A1 N1N1
[3 marks]
METHOD 1
graph of g is a quadratic function R1 N1
a quadratic function does not have any points of inflexion R1 N1
METHOD 2
graph of g is concave down over entire domain R1 N1
therefore no change in concavity R1 N1
METHOD 3
\(g”(x) = – 144\) R1 N1
therefore no points of inflexion as \(g”(x) \ne 0\) R1 N1
[2 marks]
Question
Consider a function \(f\), for \(0 \le x \le 10\). The following diagram shows the graph of \(f’\), the derivative of \(f\).
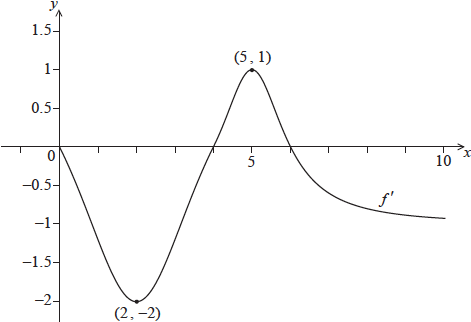
The graph of \(f’\) passes through \((2,{\text{ }} – 2)\) and \((5,{\text{ }}1)\), and has \(x\)-intercepts at \(0\), \(4\) and \(6\).
The graph of \(f\) has a local maximum point when \(x = p\). State the value of \(p\), and justify your answer.
Write down \(f'(2)\).
Let \(g(x) = \ln \left( {f(x)} \right)\) and \(f(2) = 3\).
Find \(g'(2)\).
Verify that \(\ln 3 + \int_2^a {g'(x){\text{d}}x = g(a)} \), where \(0 \le a \le 10\).
The following diagram shows the graph of \(g’\), the derivative of \(g\).
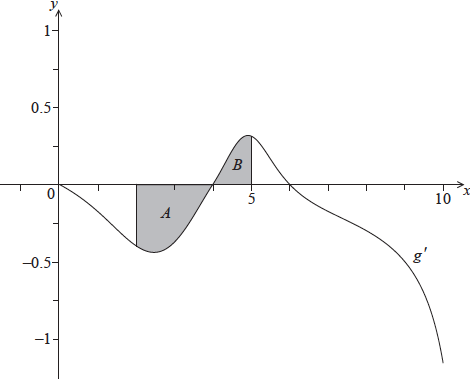
The shaded region \(A\) is enclosed by the curve, the \(x\)-axis and the line \(x = 2\), and has area \({\text{0.66 unit}}{{\text{s}}^{\text{2}}}\).
The shaded region \(B\) is enclosed by the curve, the \(x\)-axis and the line \(x = 5\), and has area \({\text{0.21 unit}}{{\text{s}}^{\text{2}}}\).
Find \(g(5)\).
Answer/Explanation
Markscheme
\(p = 6\) A1 N1
recognizing that turning points occur when \(f'(x) = 0\) R1 N1
eg\(\;\;\;\)correct sign diagram
\(f’\) changes from positive to negative at \(x = 6\) R1 N1
[3 marks]
\(f'(2) = – 2\) A1 N1
[1 mark]
attempt to apply chain rule (M1)
eg\(\;\;\;\ln (x)’ \times f'(x)\)
correct expression for \(g'(x)\) (A1)
eg\(\;\;\;g'(x) = \frac{1}{{f(x)}} \times f'(x)\)
substituting \(x = 2\) into their \(g’\) (M1)
eg\(\;\;\;\frac{{f'(2)}}{{f(2)}}\)
\( – 0.666667\)
\(g'(2) = – \frac{2}{3}{\text{ (exact), }} – 0.667\) A1 N3
[4 marks]
evidence of integrating \(g'(x)\) (M1)
eg\(\;\;\;g(x)|_2^a,{\text{ }}g(x)|_a^2\)
applying the fundamental theorem of calculus (seen anywhere) R1
eg\(\;\;\;\int_2^a {g'(x) = g(a) – g(2)} \)
correct substitution into integral (A1)
eg\(\;\;\;\ln 3 + g(a) – g(2),{\text{ }}\ln 3 + g(a) – \ln \left( {f(2)} \right)\)
\(\ln 3 + g(a) – \ln 3\) A1
\(\ln 3 + \int_2^a {g'(x) = g(a)} \) AG N0
[4 marks]
METHOD 1
substituting \(a = 5\) into the formula for \(g(a)\) (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x,{\text{ }}g(5) = \ln 3 + \int_2^5 {g'(x){\text{d}}x\;\;\;} } \left( {{\text{do not accept only }}g(5)} \right)\)
attempt to substitute areas (M1)
eg\(\;\;\;\ln 3 + 0.66 – 0.21,{\text{ }}\ln 3 + 0.66 + 0.21\)
correct working
eg\(\;\;\;g(5) = \ln 3 + ( – 0.66 + 0.21)\) (A1)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 2
attempt to set up an equation for one shaded region (M1)
eg\(\;\;\;\int_4^5 {g'(x){\text{d}}x = 0.21,{\text{ }}\int_2^4 {g'(x){\text{d}}x = – 0.66,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } } \)
two correct equations (A1)
eg\(\;\;\;g(5) – g(4) = 0.21,{\text{ }}g(2) – g(4) = 0.66\)
combining equations to eliminate \(g(4)\) (M1)
eg\(\;\;\;g(5) – [\ln 3 – 0.66] = 0.21\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 3
attempt to set up a definite integral (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x = – 0.66 + 0.21,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } \)
correct working (A1)
eg\(\;\;\;g(5) – g(2) = – 0.45\)
correct substitution (A1)
eg\(\;\;\;g(5) – \ln 3 = – 0.45\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
[4 marks]
Total [16 marks]
Question
A particle P moves along a straight line. The velocity v m s−1 of P after t seconds is given by v (t) = 7 cos t − 5t cos t, for 0 ≤ t ≤ 7.
The following diagram shows the graph of v.
Find the initial velocity of P.
Find the maximum speed of P.
Write down the number of times that the acceleration of P is 0 m s−2 .
Find the acceleration of P when it changes direction.
Find the total distance travelled by P.
Answer/Explanation
Markscheme
initial velocity when t = 0 (M1)
eg v(0)
v = 17 (m s−1) A1 N2
[2 marks]
recognizing maximum speed when \(\left| v \right|\) is greatest (M1)
eg minimum, maximum, v’ = 0
one correct coordinate for minimum (A1)
eg 6.37896, −24.6571
24.7 (ms−1) A1 N2
[3 marks]
recognizing a = v ′ (M1)
eg \(a = \frac{{{\text{d}}v}}{{{\text{d}}t}}\), correct derivative of first term
identifying when a = 0 (M1)
eg turning points of v, t-intercepts of v ′
3 A1 N3
[3 marks]
recognizing P changes direction when v = 0 (M1)
t = 0.863851 (A1)
−9.24689
a = −9.25 (ms−2) A2 N3
[4 marks]
correct substitution of limits or function into formula (A1)
eg \(\int_0^7 {\left| {\,v\,} \right|,\,\int_0^{0.8638} {v{\text{d}}t – \int_{0.8638}^7 {v{\text{d}}t} } ,\,\,\int {\left| {\,7\,{\text{cos}}\,x – 5{x^{{\text{cos}}\,x}}\,} \right|} \,dx,\,\,3.32 = 60.6} \)
63.8874
63.9 (metres) A2 N3
[3 marks]

