Download IITian Academy App for accessing Online Mock Tests and More..
Question
Consider a function \(f\), for \(0 \le x \le 10\). The following diagram shows the graph of \(f’\), the derivative of \(f\).
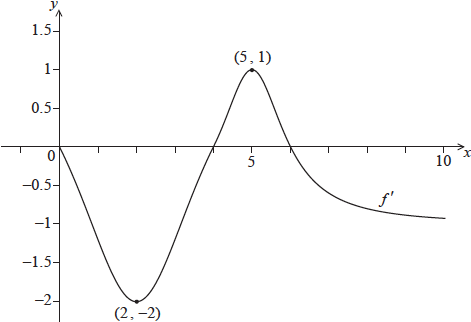
The graph of \(f’\) passes through \((2,{\text{ }} – 2)\) and \((5,{\text{ }}1)\), and has \(x\)-intercepts at \(0\), \(4\) and \(6\).
The graph of \(f\) has a local maximum point when \(x = p\). State the value of \(p\), and justify your answer.
Write down \(f'(2)\).
Let \(g(x) = \ln \left( {f(x)} \right)\) and \(f(2) = 3\).
Find \(g'(2)\).
Verify that \(\ln 3 + \int_2^a {g'(x){\text{d}}x = g(a)} \), where \(0 \le a \le 10\).
The following diagram shows the graph of \(g’\), the derivative of \(g\).
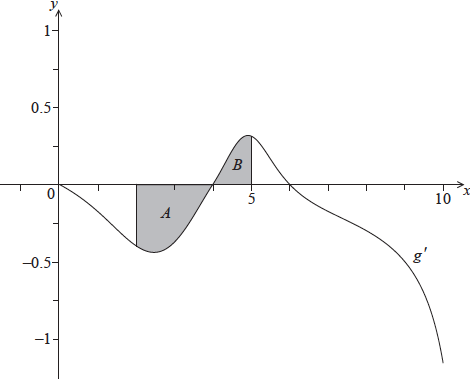
The shaded region \(A\) is enclosed by the curve, the \(x\)-axis and the line \(x = 2\), and has area \({\text{0.66 unit}}{{\text{s}}^{\text{2}}}\).
The shaded region \(B\) is enclosed by the curve, the \(x\)-axis and the line \(x = 5\), and has area \({\text{0.21 unit}}{{\text{s}}^{\text{2}}}\).
Find \(g(5)\).
Answer/Explanation
Markscheme
\(p = 6\) A1 N1
recognizing that turning points occur when \(f'(x) = 0\) R1 N1
eg\(\;\;\;\)correct sign diagram
\(f’\) changes from positive to negative at \(x = 6\) R1 N1
[3 marks]
\(f'(2) = – 2\) A1 N1
[1 mark]
attempt to apply chain rule (M1)
eg\(\;\;\;\ln (x)’ \times f'(x)\)
correct expression for \(g'(x)\) (A1)
eg\(\;\;\;g'(x) = \frac{1}{{f(x)}} \times f'(x)\)
substituting \(x = 2\) into their \(g’\) (M1)
eg\(\;\;\;\frac{{f'(2)}}{{f(2)}}\)
\( – 0.666667\)
\(g'(2) = – \frac{2}{3}{\text{ (exact), }} – 0.667\) A1 N3
[4 marks]
evidence of integrating \(g'(x)\) (M1)
eg\(\;\;\;g(x)|_2^a,{\text{ }}g(x)|_a^2\)
applying the fundamental theorem of calculus (seen anywhere) R1
eg\(\;\;\;\int_2^a {g'(x) = g(a) – g(2)} \)
correct substitution into integral (A1)
eg\(\;\;\;\ln 3 + g(a) – g(2),{\text{ }}\ln 3 + g(a) – \ln \left( {f(2)} \right)\)
\(\ln 3 + g(a) – \ln 3\) A1
\(\ln 3 + \int_2^a {g'(x) = g(a)} \) AG N0
[4 marks]
METHOD 1
substituting \(a = 5\) into the formula for \(g(a)\) (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x,{\text{ }}g(5) = \ln 3 + \int_2^5 {g'(x){\text{d}}x\;\;\;} } \left( {{\text{do not accept only }}g(5)} \right)\)
attempt to substitute areas (M1)
eg\(\;\;\;\ln 3 + 0.66 – 0.21,{\text{ }}\ln 3 + 0.66 + 0.21\)
correct working
eg\(\;\;\;g(5) = \ln 3 + ( – 0.66 + 0.21)\) (A1)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 2
attempt to set up an equation for one shaded region (M1)
eg\(\;\;\;\int_4^5 {g'(x){\text{d}}x = 0.21,{\text{ }}\int_2^4 {g'(x){\text{d}}x = – 0.66,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } } \)
two correct equations (A1)
eg\(\;\;\;g(5) – g(4) = 0.21,{\text{ }}g(2) – g(4) = 0.66\)
combining equations to eliminate \(g(4)\) (M1)
eg\(\;\;\;g(5) – [\ln 3 – 0.66] = 0.21\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 3
attempt to set up a definite integral (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x = – 0.66 + 0.21,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } \)
correct working (A1)
eg\(\;\;\;g(5) – g(2) = – 0.45\)
correct substitution (A1)
eg\(\;\;\;g(5) – \ln 3 = – 0.45\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
[4 marks]
Total [16 marks]
Question
A particle P moves along a straight line. Its velocity \({v_{\text{P}}}{\text{ m}}\,{{\text{s}}^{ – 1}}\) after \(t\) seconds is given by \({v_{\text{P}}} = \sqrt t \sin \left( {\frac{\pi }{2}t} \right)\), for \(0 \leqslant t \leqslant 8\). The following diagram shows the graph of \({v_{\text{P}}}\).
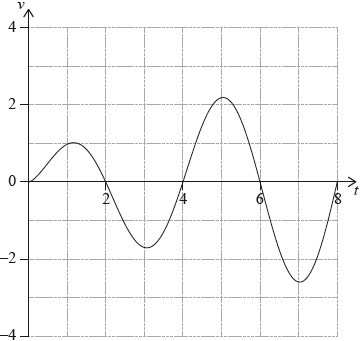
Write down the first value of \(t\) at which P changes direction.
Find the total distance travelled by P, for \(0 \leqslant t \leqslant 8\).
A second particle Q also moves along a straight line. Its velocity, \({v_{\text{Q}}}{\text{ m}}\,{{\text{s}}^{ – 1}}\) after \(t\) seconds is given by \({v_{\text{Q}}} = \sqrt t \) for \(0 \leqslant t \leqslant 8\). After \(k\) seconds Q has travelled the same total distance as P.
Find \(k\).
Answer/Explanation
Markscheme
\(t = 2\) A1 N1
[1 mark]
substitution of limits or function into formula or correct sum (A1)
eg\(\,\,\,\,\,\)\(\int_0^8 {\left| v \right|{\text{d}}t,{\text{ }}\int {\left| {{v_Q}} \right|{\text{d}}t,{\text{ }}\int_0^2 {v{\text{d}}t – \int_2^4 {v{\text{d}}t + \int_4^6 {v{\text{d}}t – \int_6^8 {v{\text{d}}t} } } } } } \)
9.64782
distance \( = 9.65{\text{ (metres)}}\) A1 N2
[2 marks]
correct approach (A1)
eg\(\,\,\,\,\,\)\(s = \int {\sqrt t ,{\text{ }}\int_0^k {\sqrt t } } {\text{d}}t,{\text{ }}\int_0^k {\left| {{v_{\text{Q}}}} \right|{\text{d}}t} \)
correct integration (A1)
eg\(\,\,\,\,\,\)\(\int {\sqrt t = \frac{2}{3}{t^{\frac{3}{2}}} + c,{\text{ }}\left[ {\frac{2}{3}{x^{\frac{3}{2}}}} \right]_0^k,{\text{ }}\frac{2}{3}{k^{\frac{3}{2}}}} \)
equating their expression to the distance travelled by their P (M1)
eg\(\,\,\,\,\,\)\(\frac{2}{3}{k^{\frac{3}{2}}} = 9.65,{\text{ }}\int_0^k {\sqrt t {\text{d}}t = 9.65} \)
5.93855
5.94 (seconds) A1 N3
[4 marks]