Question
a.Show that \(\cot \alpha = \tan \left( {\frac{\pi }{2} – \alpha } \right)\) for \(0 < \alpha < \frac{\pi }{2}\).[1]
b.Hence find \(\int_{\tan \alpha }^{\cot \alpha } {\frac{1}{{1 + {x^2}}}{\text{d}}x,{\text{ }}0 < \alpha < \frac{\pi }{2}} \).[4]
▶️Answer/Explanation
Markscheme
EITHER
use of a diagram and trig ratios
eg,
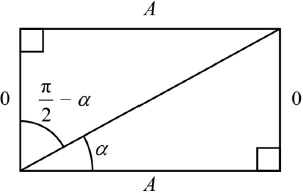
\(\tan \alpha = \frac{O}{A} \Rightarrow \cot \alpha = \frac{A}{O}\)
from diagram, \(\tan \left( {\frac{\pi }{2} – \alpha } \right) = \frac{A}{O}\) R1
OR
use of \(\tan \left( {\frac{\pi }{2} – \alpha } \right) = \frac{{\sin \left( {\frac{\pi }{2} – \alpha } \right)}}{{\cos \left( {\frac{\pi }{2} – \alpha } \right)}} = \frac{{\cos \alpha }}{{\sin \alpha }}\) R1
THEN
\(\cot \alpha = \tan \left( {\frac{\pi }{2} – \alpha } \right)\) AG
[1 mark]
\(\int_{\tan \alpha }^{\cot \alpha } {\frac{1}{{1 + {x^2}}}{\text{d}}x} = [\arctan x]_{\tan \alpha }^{\cot \alpha }\) (A1)
Note: Limits (or absence of such) may be ignored at this stage.
\( = \arctan (\cot \alpha ) – \arctan (\tan \alpha )\) (M1)
\( = \frac{\pi }{2} – \alpha – \alpha \) (A1)
\( = \frac{\pi }{2} – 2\alpha \) A1
[4 marks]
Examiners report
This was generally well done.
This was generally well done. Some weaker candidates tried to solve part (b) through use of a substitution, though the standard result \(\arctan x\) was well known. A small number used \(\arctan x + c\) and went on to obtain an incorrect final answer.
Question
Consider the function \(f(x) = \frac{1}{{{x^2} + 3x + 2}},{\text{ }}x \in \mathbb{R},{\text{ }}x \ne – 2,{\text{ }}x \ne – 1\).
a.i.Express \({x^2} + 3x + 2\) in the form \({(x + h)^2} + k\).[1]
a.ii.Factorize \({x^2} + 3x + 2\).[1]
b.Sketch the graph of \(f(x)\), indicating on it the equations of the asymptotes, the coordinates of the \(y\)-intercept and the local maximum.[5]
c.Show that \(\frac{1}{{x + 1}} – \frac{1}{{x + 2}} = \frac{1}{{{x^2} + 3x + 2}}\).[1]
d.Hence find the value of \(p\) if \(\int_0^1 {f(x){\text{d}}x = \ln (p)} \).[4
e.Sketch the graph of \(y = f\left( {\left| x \right|} \right)\).[2]
f.Determine the area of the region enclosed between the graph of \(y = f\left( {\left| x \right|} \right)\), the \(x\)-axis and the lines with equations \(x = – 1\) and \(x = 1\).[3]
▶️Answer/Explanation
Markscheme
\({x^2} + 3x + 2 = {\left( {x + \frac{3}{2}} \right)^2} – \frac{1}{4}\) A1
[1 mark]
\({x^2} + 3x + 2 = (x + 2)(x + 1)\) A1
[1 mark]
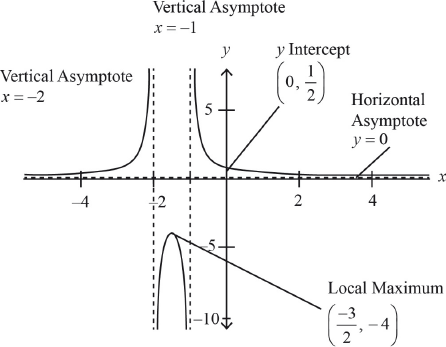
A1 for the shape
A1 for the equation \(y = 0\)
A1 for asymptotes \(x = – 2\) and \(x = – 1\)
A1 for coordinates \(\left( { – \frac{3}{2},{\text{ }} – 4} \right)\)
A1 \(y\)-intercept \(\left( {0,{\text{ }}\frac{1}{2}} \right)\)
[5 marks]
\(\frac{1}{{x + 1}} – \frac{1}{{x + 2}} = \frac{{(x + 2) – (x + 1)}}{{(x + 1)(x + 2)}}\) M1
\( = \frac{1}{{{x^2} + 3x + 2}}\) AG
[1 mark]
\(\int\limits_0^1 {\frac{1}{{x + 1}} – \frac{1}{{x + 2}}{\text{d}}x} \)
\( = \left[ {\ln (x + 1) – \ln (x + 2)} \right]_0^1\) A1
\( = \ln 2 – \ln 3 – \ln 1 + \ln 2\) M1
\( = \ln \left( {\frac{4}{3}} \right)\) M1A1
\(\therefore p = \frac{4}{3}\)
[4 marks]
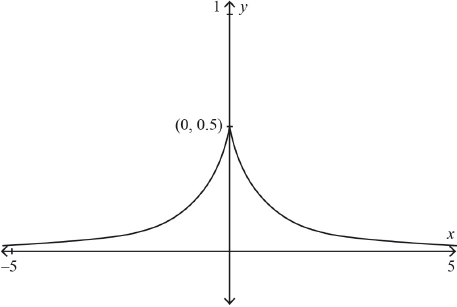
symmetry about the \(y\)-axis M1
correct shape A1
Note: Allow FT from part (b).
[2 marks]
\(2\int_0^1 {f(x){\text{d}}x} \) (M1)(A1)
\( = 2\ln \left( {\frac{4}{3}} \right)\) A1
Note: Do not award FT from part (e).
[3 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
Consider the functions \(f,\,\,g,\) defined for \(x \in \mathbb{R}\), given by \(f\left( x \right) = {{\text{e}}^{ – x}}\,{\text{sin}}\,x\) and \(g\left( x \right) = {{\text{e}}^{ – x}}\,{\text{cos}}\,x\).
a.i.Find \(f’\left( x \right)\).[2]
a.ii.Find \(g’\left( x \right)\).[1]
b.Hence, or otherwise, find \(\int\limits_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x} \).[4]
▶️Answer/Explanation
Markscheme
attempt at product rule M1
\(f’\left( x \right) = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x + {{\text{e}}^{ – x}}\,{\text{cos}}\,x\) A1
[2 marks]
\(g’\left( x \right) = – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – {{\text{e}}^{ – x}}\,{\text{sin}}\,x\) A1
[1 mark]
METHOD 1
Attempt to add \(f’\left( x \right)\) and \(g’\left( x \right)\) (M1)
\(f’\left( x \right) + g’\left( x \right) = – 2{{\text{e}}^{ – x}}\,{\text{sin}}\,x\) A1
\(\int\limits_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x} = \left[ { – \frac{{{{\text{e}}^{ – x}}}}{2}\left( {{\text{sin}}\,x + {\text{cos}}\,x} \right)} \right]_0^\pi \) (or equivalent) A1
Note: Condone absence of limits.
\( = \frac{1}{2}\left( {1 + {{\text{e}}^{ – \pi }}} \right)\) A1
METHOD 2
\(I = \int {{{\text{e}}^{ – x}}} \,{\text{sin}}\,x\,{\text{d}}x\)
\( = – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – \int {{{\text{e}}^{ – x}}} \,{\text{cos}}\,x\,{\text{d}}x\) OR \( = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x + \int {{{\text{e}}^{ – x}}} \,{\text{cos}}\,x\,{\text{d}}x\) M1A1
\( = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – \int {{{\text{e}}^{ – x}}} \,{\text{sin}}\,x\,{\text{d}}x\)
\(I = \frac{1}{2}{{\text{e}}^{ – x}}\left( {{\text{sin}}\,x + {\text{cos}}\,x} \right)\) A1
\(\int_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x = \frac{1}{2}\left( {1 + {{\text{e}}^{ – \pi }}} \right)} \) A1
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
