Download IITian Academy App for accessing Online Mock Tests and More..
Question
Let \(f(x) = {{\rm{e}}^x}(1 – {x^2})\) .
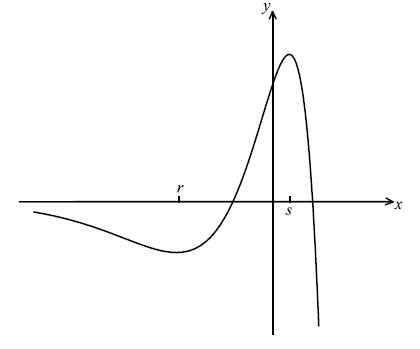
Part of the graph of \(y = f(x)\), for \( – 6 \le x \le 2\) , is shown below. The x-coordinates of the local minimum and maximum points are r and s respectively.
Show that \(f'(x) = {{\rm{e}}^x}(1 – 2x – {x^2})\) .
Write down the equation of the horizontal asymptote.
Write down the value of r and of s.
Let L be the normal to the curve of f at \({\text{P}}(0{\text{, }}1)\) . Show that L has equation \(x + y = 1\) .
Let R be the region enclosed by the curve \(y = f(x)\) and the line L.
(i) Find an expression for the area of R.
(ii) Calculate the area of R.
Answer/Explanation
Markscheme
evidence of using the product rule M1
\(f'(x) = {{\rm{e}}^x}(1 – {x^2}) + {{\rm{e}}^x}( – 2x)\) A1A1
Note: Award A1 for \({{\rm{e}}^x}(1 – {x^2})\) , A1 for \({{\rm{e}}^x}( – 2x)\) .
\(f'(x) = {{\rm{e}}^x}(1 – 2x – {x^2})\) AG N0
[3 marks]
\(y = 0\) A1 N1
[1 mark]
at the local maximum or minimum point
\(f'(x) = 0\) \(({{\rm{e}}^x}(1 – 2x – {x^2}) = 0)\) (M1)
\( \Rightarrow 1 – 2x – {x^2} = 0\) (M1)
\(r = – 2.41\) \(s = 0.414\) A1A1 N2N2
[4 marks]
\(f'(0) = 1\) A1
gradient of the normal \(= – 1\) A1
evidence of substituting into an equation for a straight line (M1)
correct substitution A1
e.g. \(y – 1 = – 1(x – 0)\) , \(y – 1 = – x\) , \(y = – x + 1\)
\(x + y = 1\) AG N0
[4 marks]
(i) intersection points at \(x = 0\) and \(x = 1\) (may be seen as the limits) (A1)
approach involving subtraction and integrals (M1)
fully correct expression A2 N4
e.g. \(\int_0^1 {\left( {{{\rm{e}}^x}(1 – {x^2}) – (1 – x)} \right)} {\rm{d}}x\) , \(\int_0^1 {f(x){\rm{d}}x – \int_0^1 {(1 – x){\rm{d}}x} } \)
(ii) area \(R = 0.5\) A1 N1
[5 marks]
Question
Let \(f(x) = {{\rm{e}}^{2x}}\cos x\) , \( – 1 \le x \le 2\) .
Show that \(f'(x) = {{\rm{e}}^{2x}}(2\cos x – \sin x)\) .
Let the line L be the normal to the curve of f at \(x = 0\) .
Find the equation of L .
The graph of f and the line L intersect at the point (0, 1) and at a second point P.
(i) Find the x-coordinate of P.
(ii) Find the area of the region enclosed by the graph of f and the line L .
Answer/Explanation
Markscheme
correctly finding the derivative of \({{\rm{e}}^{2x}}\) , i.e. \(2{{\rm{e}}^{2x}}\) A1
correctly finding the derivative of \(\cos x\) , i.e. \( – \sin x\) A1
evidence of using the product rule, seen anywhere M1
e.g. \(f'(x) = 2{{\rm{e}}^{2x}}\cos x – {{\rm{e}}^{2x}}\sin x\)
\(f'(x) = 2{{\rm{e}}^{2x}}(2\cos x – \sin x)\) AG N0
[3 marks]
evidence of finding \(f(0) = 1\) , seen anywhere A1
attempt to find the gradient of f (M1)
e.g. substituting \(x = 0\) into \(f'(x)\)
value of the gradient of f A1
e.g. \(f'(0) = 2\) , equation of tangent is \(y = 2x + 1\)
gradient of normal \( = – \frac{1}{2}\) (A1)
\(y – 1 = – \frac{1}{2}x\left( {y = – \frac{1}{2}x + 1} \right)\) A1 N3
[5 marks]
(i) evidence of equating correct functions M1
e.g. \({{\rm{e}}^{2x}}\cos x = – \frac{1}{2}x + 1\) , sketch showing intersection of graphs
\(x = 1.56\) A1 N1
(ii) evidence of approach involving subtraction of integrals/areas (M1)
e.g. \(\int {\left[ {f(x) – g(x)} \right]} {\rm{d}}x\) , \(\int {f(x)} {\rm{d}}x – {\text{area under trapezium}}\)
fully correct integral expression A2
e.g. \(\int_0^{1.56} {\left[ {{{\rm{e}}^{2x}}\cos x – \left( { – \frac{1}{2}x + 1} \right)} \right]} {\rm{d}}x\) , \(\int_0^{1.56} {{{\rm{e}}^{2x}}\cos x} {\rm{d}}x – 0.951 \ldots \)
\({\rm{area}} = 3.28\) A1 N2
[6 marks]
Question
Let \(f(x) = 5\cos \frac{\pi }{4}x\) and \(g(x) = – 0.5{x^2} + 5x – 8\) for \(0 \le x \le 9\) .
On the same diagram, sketch the graphs of f and g .
Consider the graph of \(f\) . Write down
(i) the x-intercept that lies between \(x = 0\) and \(x = 3\) ;
(ii) the period;
(iii) the amplitude.
Consider the graph of g . Write down
(i) the two x-intercepts;
(ii) the equation of the axis of symmetry.
Let R be the region enclosed by the graphs of f and g . Find the area of R.
Answer/Explanation
Markscheme
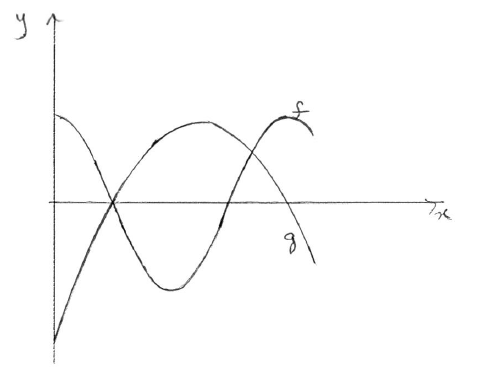A1A1A1 N3
Note: Award A1 for f being of sinusoidal shape, with 2 maxima and one minimum, A1 for g being a parabola opening down, A1 for two intersection points in approximately correct position.
[3 marks]
(i) \((2{\text{, }}0)\) (accept \(x = 2\) ) A1 N1
(ii) \({\text{period}} = 8\) A2 N2
(iii) \({\text{amplitude}} = 5\) A1 N1
[4 marks]
(i) \((2{\text{, }}0)\) , \((8{\text{, }}0)\) (accept \(x = 2\) , \(x = 8\) ) A1A1 N1N1
(ii) \(x = 5\) (must be an equation) A1 N1
[3 marks]
METHOD 1
intersect when \(x = 2\) and \(x = 6.79\) (may be seen as limits of integration) A1A1
evidence of approach (M1)
e.g. \(\int {g – f} \) , \(\int {f(x){\rm{d}}x – \int {g(x){\rm{d}}x}}\) , \(\int_2^{6.79} {\left( {( – 0.5{x^2} + 5x – 8) – \left( {5\cos \frac{\pi }{4}x} \right)} \right)}\)
\({\text{area}} = 27.6\) A2 N3
METHOD 2
intersect when \(x = 2\) and \(x = 6.79\) (seen anywhere) A1A1
evidence of approach using a sketch of g and f , or \(g – f\) . (M1)
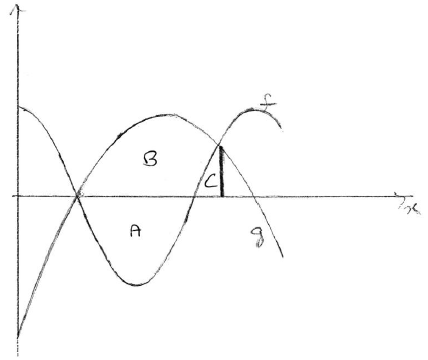
e.g. area = \(A + B – C\) , \(12.7324 + 16.0938 – 1.18129 \ldots \)
\({\text{area}} = 27.6\) A2 N3
[5 marks]
Question
Let \(f(x) = \cos ({x^2})\) and \(g(x) = {{\rm{e}}^x}\) , for \( – 1.5 \le x \le 0.5\) .
Find the area of the region enclosed by the graphs of f and g .
Answer/Explanation
Markscheme
evidence of finding intersection points (M1)
e.g. \(f(x) = g(x)\) , \(\cos {x^2} = {{\rm{e}}^x}\) , sketch showing intersection
\(x = – 1.11\) , \(x = 0\) (may be seen as limits in the integral) A1A1
evidence of approach involving integration and subtraction (in any order) (M1)
e.g. \(\int_{ – 1.11}^0 {\cos {x^2} – {{\rm{e}}^x}} \) , \(\int {(\cos {x^2} – {{\rm{e}}^x}){\rm{d}}x} \) , \(\int {g – f} \)
\({\text{area}} = 0.282\) A2 N3
[6 marks]
Question
Consider the function \(f(x) = {x^2} – 4x + 1\) .
Sketch the graph of f , for \( – 1 \le x \le 5\) .
This function can also be written as \(f(x) = {(x – p)^2} – 3\) .
Write down the value of p .
The graph of g is obtained by reflecting the graph of f in the x-axis, followed by a translation of \(\left( {\begin{array}{*{20}{c}}
0\\
6
\end{array}} \right)\) .
Show that \(g(x) = – {x^2} + 4x + 5\) .
The graph of g is obtained by reflecting the graph of f in the x-axis, followed by a translation of \(\left( {\begin{array}{*{20}{c}}
0\\
6
\end{array}} \right)\) .
The graphs of f and g intersect at two points.
Write down the x-coordinates of these two points.
The graph of \(g\) is obtained by reflecting the graph of \(f\) in the x-axis, followed by a translation of \(\left( {\begin{array}{*{20}{c}}
0 \\
6
\end{array}} \right)\) .
Let R be the region enclosed by the graphs of f and g .
Find the area of R .
Answer/Explanation
Markscheme
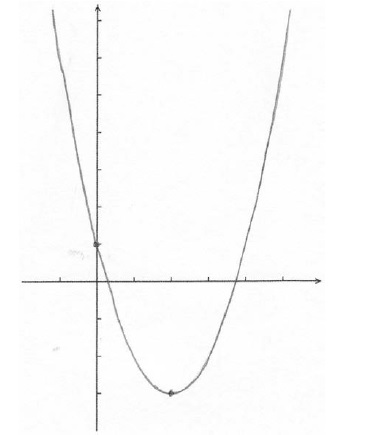A1A1A1A1 N4
Note: The shape must be an approximately correct upwards parabola.
Only if the shape is approximately correct, award the following:
A1 for vertex \(x \approx 2\) , A1 for x-intercepts between 0 and 1, and 3 and 4, A1 for correct y-intercept \((0{\text{, }}1)\), A1 for correct domain \([ – 1{\text{, }}5]\).
Scale not required on the axes, but approximate positions need to be clear.
[4 marks]
\(p = 2\) A1 N1
[1 mark]
correct vertical reflection, correct vertical translation (A1)(A1)
e.g. \( – f(x)\) , \( – ({(x – 2)^2} – 3)\) , \( – y\) , \( – f(x) + 6\) , \(y + 6\)
transformations in correct order (A1)
e.g. \( – ({x^2} – 4x + 1) + 6\) , \( – ({(x – 2)^2} – 3) + 6\)
simplification which clearly leads to given answer A1
e.g. \( – {x^2} + 4x – 1 + 6\) , \( – ({x^2} – 4x + 4 – 3) + 6\)
\(g(x) = – {x^2} + 4x + 5\) AG N0
Note: If working shown, award A1A1A0A0 if transformations correct, but done in reverse order, e.g. \( – ({x^2} – 4x + 1 + 6)\).
[4 marks]
valid approach (M1)
e.g. sketch, \(f = g\)
\( – 0.449489 \ldots \) , \(4.449489 \ldots \)
\((2 \pm \sqrt 6 )\) (exact), \( – 0.449{\text{ }}[ – 0.450{\text{, }} – 0.449]\) ; \(4.45{\text{ }}[4.44{\text{, }}4.45]\) A1A1 N3
[3 marks]
attempt to substitute limits or functions into area formula (accept absence of \({\rm{d}}x\) ) (M1)
e.g. \(\int_a^b {(( – {x^2}} + 4x + 5) – ({x^2} – 4x + 1)){\rm{d}}x\) , \(\int_{4.45}^{ – 0.449} {(f – g)} \) , \(\int {( – 2{x^2}} + 8x + 4){\rm{d}}x\)
approach involving subtraction of integrals/areas (accept absence of \({\rm{d}}x\) ) (M1)
e.g. \(\int_a^b {( – {x^2}} + 4x + 5) – \int_a^b {({x^2}} – 4x + 1)\) , \(\int {(f – g){\rm{d}}x} \)
\({\rm{area}} = 39.19183 \ldots \)
\({\rm{area}} = 39.2\) \([39.1{\text{, }}39.2]\) A1 N3
[3 marks]
Question
Let \(f(x) = {x^2}\) and \(g(x) = 3\ln (x + 1)\), for \(x > – 1\).
Solve \(f(x) = g(x)\).
Find the area of the region enclosed by the graphs of \(f\) and \(g\).
Answer/Explanation
Markscheme
valid approach (M1)
eg sketch
0, 1.73843
\(x = 0,{\text{ }}x = 1.74{\text{ }}\left( {{\text{accept }}(0,{\text{ }}0){\text{ and }}(1.74,{\text{ }}3.02)} \right)\) A1A1 N3
[3 marks]
integrating and subtracting functions (in any order) (M1)
eg\(\,\,\,\,\,\)\(\int {g – f} \)
correct substitution of their limits or function (accept missing \({\text{d}}x\))
(A1)
eg\(\,\,\,\,\,\)\(\int_0^{1.74} {g – f,{\text{ }}\int {3\ln (x + 1) – {x^2}} } \)
Note: Do not award A1 if there is an error in the substitution.
1.30940
1.31 A1 N3
[3 marks]
Question
Let \(f(x) = x{{\text{e}}^{ – x}}\) and \(g(x) = – 3f(x) + 1\).
The graphs of \(f\) and \(g\) intersect at \(x = p\) and \(x = q\), where \(p < q\).
Find the value of \(p\) and of \(q\).
Hence, find the area of the region enclosed by the graphs of \(f\) and \(g\).
Answer/Explanation
Markscheme
valid attempt to find the intersection (M1)
eg\(\,\,\,\,\,\)\(f = g\), sketch, one correct answer
\(p = 0.357402,{\text{ }}q = 2.15329\)
\(p = 0.357,{\text{ }}q = 2.15\) A1A1 N3
[3 marks]
attempt to set up an integral involving subtraction (in any order) (M1)
eg\(\,\,\,\,\,\)\(\int_p^q {\left[ {f(x) – g(x)} \right]{\text{d}}x,{\text{ }}} \int_p^q {f(x){\text{d}}x – } \int_p^q {g(x){\text{d}}x} \)
0.537667
\({\text{area}} = 0.538\) A2 N3
[3 marks]
Question
Let \(f(x) = \ln x\) and \(g(x) = 3 + \ln \left( {\frac{x}{2}} \right)\), for \(x > 0\).
The graph of \(g\) can be obtained from the graph of \(f\) by two transformations:
\[\begin{array}{*{20}{l}} {{\text{a horizontal stretch of scale factor }}q{\text{ followed by}}} \\ {{\text{a translation of }}\left( {\begin{array}{*{20}{c}} h \\ k \end{array}} \right).} \end{array}\]
Let \(h(x) = g(x) \times \cos (0.1x)\), for \(0 < x < 4\). The following diagram shows the graph of \(h\) and the line \(y = x\).
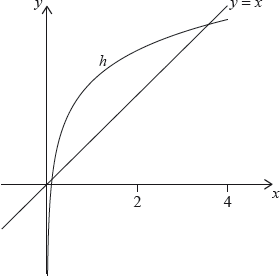
The graph of \(h\) intersects the graph of \({h^{ – 1}}\) at two points. These points have \(x\) coordinates 0.111 and 3.31 correct to three significant figures.
Write down the value of \(q\);
Write down the value of \(h\);
Write down the value of \(k\).
Find \(\int_{0.111}^{3.31} {\left( {h(x) – x} \right){\text{d}}x} \).
Hence, find the area of the region enclosed by the graphs of \(h\) and \({h^{ – 1}}\).
Let \(d\) be the vertical distance from a point on the graph of \(h\) to the line \(y = x\). There is a point \({\text{P}}(a,{\text{ }}b)\) on the graph of \(h\) where \(d\) is a maximum.
Find the coordinates of P, where \(0.111 < a < 3.31\).
Answer/Explanation
Markscheme
\(q = 2\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
\(h = 0\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
\(k = 3\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
2.72409
2.72 A2 N2
[2 marks]
recognizing area between \(y = x\) and \(h\) equals 2.72 (M1)
eg\(\,\,\,\,\,\)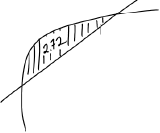
recognizing graphs of \(h\) and \({h^{ – 1}}\) are reflections of each other in \(y = x\) (M1)
eg\(\,\,\,\,\,\)area between \(y = x\) and \(h\) equals between \(y = x\) and \({h^{ – 1}}\)
\(2 \times 2.72\int_{0.111}^{3.31} {\left( {x – {h^{ – 1}}(x)} \right){\text{d}}x = 2.72} \)
5.44819
5.45 A1 N3
[??? marks]
valid attempt to find \(d\) (M1)
eg\(\,\,\,\,\,\)difference in \(y\)-coordinates, \(d = h(x) – x\)
correct expression for \(d\) (A1)
eg\(\,\,\,\,\,\)\(\left( {\ln \frac{1}{2}x + 3} \right)(\cos 0.1x) – x\)
valid approach to find when \(d\) is a maximum (M1)
eg\(\,\,\,\,\,\)max on sketch of \(d\), attempt to solve \(d’ = 0\)
0.973679
\(x = 0.974\) A2 N4
substituting their \(x\) value into \(h(x)\) (M1)
2.26938
\(y = 2.27\) A1 N2
[7 marks]
Question
Let g(x) = −(x − 1)2 + 5.
Let f(x) = x2. The following diagram shows part of the graph of f.
The graph of g intersects the graph of f at x = −1 and x = 2.
Write down the coordinates of the vertex of the graph of g.
On the grid above, sketch the graph of g for −2 ≤ x ≤ 4.
Find the area of the region enclosed by the graphs of f and g.
Answer/Explanation
Markscheme
(1,5) (exact) A1 N1
[1 mark]
A1A1A1 N3
Note: The shape must be a concave-down parabola.
Only if the shape is correct, award the following for points in circles:
A1 for vertex,
A1 for correct intersection points,
A1 for correct endpoints.
[3 marks]
integrating and subtracting functions (in any order) (M1)
eg \(\int {f – g} \)
correct substitution of limits or functions (accept missing dx, but do not accept any errors, including extra bits) (A1)
eg \(\int_{ – 1}^2 {g – f,\,\,\int { – {{\left( {x – 1} \right)}^2}} } + 5 – {x^2}\)
area = 9 (exact) A1 N2
[3 marks]