Download IITian Academy App for accessing Online Mock Tests and More..
Question
Let \(f(x) = {{\rm{e}}^x}\sin 2x + 10\) , for \(0 \le x \le 4\) . Part of the graph of f is given below.
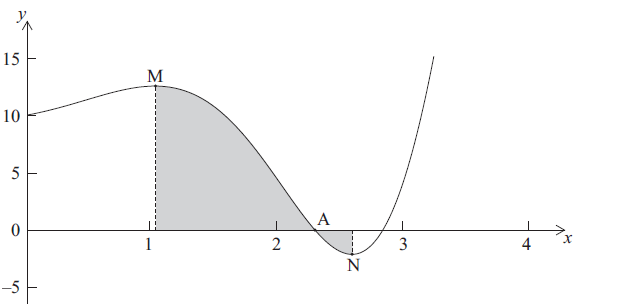
There is an x-intercept at the point A, a local maximum point at M, where \(x = p\) and a local minimum point at N, where \(x = q\) .
Write down the x-coordinate of A.
Find the value of
(i) p ;
(ii) q .
Find \(\int_p^q {f(x){\rm{d}}x} \) . Explain why this is not the area of the shaded region.
Answer/Explanation
Markscheme
\(2.31\) A1 N1
[1 mark]
(i) 1.02 A1 N1
(ii) 2.59 A1 N1
[2 marks]
\(\int_p^q {f(x){\rm{d}}x} = 9.96\) A1 N1
split into two regions, make the area below the x-axis positive R1R1 N2
[3 marks]
Question
Let \(f(x) = x\ln (4 – {x^2})\) , for \( – 2 < x < 2\) . The graph of f is shown below.
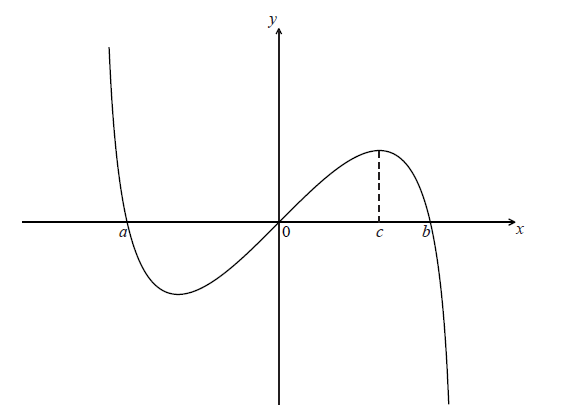
The graph of f crosses the x-axis at \(x = a\) , \(x = 0\) and \(x = b\) .
Find the value of a and of b .
The graph of f has a maximum value when \(x = c\) .
Find the value of c .
The region under the graph of f from \(x = 0\) to \(x = c\) is rotated \({360^ \circ }\) about the x-axis. Find the volume of the solid formed.
Let R be the region enclosed by the curve, the x-axis and the line \(x = c\) , between \(x = a\) and \(x = c\) .
Find the area of R .
Answer/Explanation
Markscheme
evidence of valid approach (M1)
e.g. \(f(x) = 0\) , graph
\(a = – 1.73\) , \(b = 1.73\) \((a = – \sqrt 3 {\text{, }}b = \sqrt 3 )\) A1A1 N3
[3 marks]
attempt to find max (M1)
e.g. setting \(f'(x) = 0\) , graph
\(c = 1.15\) (accept (1.15, 1.13)) A1 N2
[2 marks]
attempt to substitute either limits or the function into formula M1
e.g. \(V = \pi {\int_0^c {\left[ {f(x)} \right]} ^2}{\rm{d}}x\) , \(\pi {\int {\left[ {x\ln (4 – {x^2})} \right]} ^2}\) , \(\pi \int_0^{1.149 \ldots } {{y^2}{\rm{d}}x} \)
\(V = 2.16\) A2 N2
[3 marks]
valid approach recognizing 2 regions (M1)
e.g. finding 2 areas
correct working (A1)
e.g. \(\int_0^{ – 1.73 \ldots } {f(x){\rm{d}}x + } \int_0^{1.149 \ldots } {f(x){\rm{d}}x} \) , \( – \int_{ – 1.73 \ldots }^0 {f(x){\rm{d}}x + } \int_0^{1.149 \ldots } {f(x){\rm{d}}x} \)
area \( = 2.07\) (accept 2.06) A2 N3
[4 marks]
Question
Consider a function \(f\), for \(0 \le x \le 10\). The following diagram shows the graph of \(f’\), the derivative of \(f\).
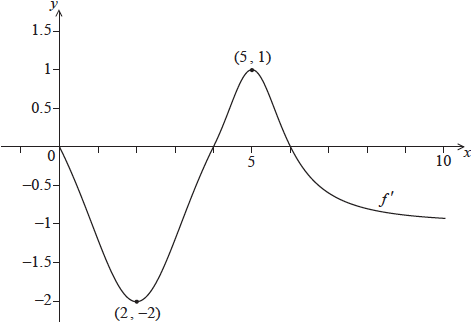
The graph of \(f’\) passes through \((2,{\text{ }} – 2)\) and \((5,{\text{ }}1)\), and has \(x\)-intercepts at \(0\), \(4\) and \(6\).
The graph of \(f\) has a local maximum point when \(x = p\). State the value of \(p\), and justify your answer.
Write down \(f'(2)\).
Let \(g(x) = \ln \left( {f(x)} \right)\) and \(f(2) = 3\).
Find \(g'(2)\).
Verify that \(\ln 3 + \int_2^a {g'(x){\text{d}}x = g(a)} \), where \(0 \le a \le 10\).
The following diagram shows the graph of \(g’\), the derivative of \(g\).
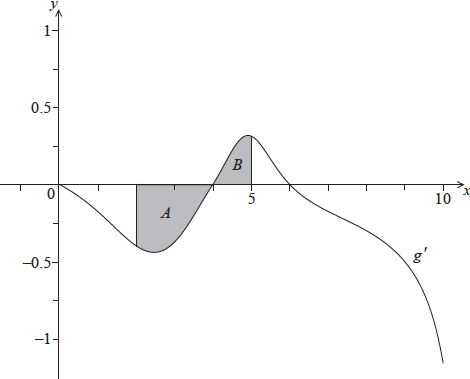
The shaded region \(A\) is enclosed by the curve, the \(x\)-axis and the line \(x = 2\), and has area \({\text{0.66 unit}}{{\text{s}}^{\text{2}}}\).
The shaded region \(B\) is enclosed by the curve, the \(x\)-axis and the line \(x = 5\), and has area \({\text{0.21 unit}}{{\text{s}}^{\text{2}}}\).
Find \(g(5)\).
Answer/Explanation
Markscheme
\(p = 6\) A1 N1
recognizing that turning points occur when \(f'(x) = 0\) R1 N1
eg\(\;\;\;\)correct sign diagram
\(f’\) changes from positive to negative at \(x = 6\) R1 N1
[3 marks]
\(f'(2) = – 2\) A1 N1
[1 mark]
attempt to apply chain rule (M1)
eg\(\;\;\;\ln (x)’ \times f'(x)\)
correct expression for \(g'(x)\) (A1)
eg\(\;\;\;g'(x) = \frac{1}{{f(x)}} \times f'(x)\)
substituting \(x = 2\) into their \(g’\) (M1)
eg\(\;\;\;\frac{{f'(2)}}{{f(2)}}\)
\( – 0.666667\)
\(g'(2) = – \frac{2}{3}{\text{ (exact), }} – 0.667\) A1 N3
[4 marks]
evidence of integrating \(g'(x)\) (M1)
eg\(\;\;\;g(x)|_2^a,{\text{ }}g(x)|_a^2\)
applying the fundamental theorem of calculus (seen anywhere) R1
eg\(\;\;\;\int_2^a {g'(x) = g(a) – g(2)} \)
correct substitution into integral (A1)
eg\(\;\;\;\ln 3 + g(a) – g(2),{\text{ }}\ln 3 + g(a) – \ln \left( {f(2)} \right)\)
\(\ln 3 + g(a) – \ln 3\) A1
\(\ln 3 + \int_2^a {g'(x) = g(a)} \) AG N0
[4 marks]
METHOD 1
substituting \(a = 5\) into the formula for \(g(a)\) (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x,{\text{ }}g(5) = \ln 3 + \int_2^5 {g'(x){\text{d}}x\;\;\;} } \left( {{\text{do not accept only }}g(5)} \right)\)
attempt to substitute areas (M1)
eg\(\;\;\;\ln 3 + 0.66 – 0.21,{\text{ }}\ln 3 + 0.66 + 0.21\)
correct working
eg\(\;\;\;g(5) = \ln 3 + ( – 0.66 + 0.21)\) (A1)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 2
attempt to set up an equation for one shaded region (M1)
eg\(\;\;\;\int_4^5 {g'(x){\text{d}}x = 0.21,{\text{ }}\int_2^4 {g'(x){\text{d}}x = – 0.66,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } } \)
two correct equations (A1)
eg\(\;\;\;g(5) – g(4) = 0.21,{\text{ }}g(2) – g(4) = 0.66\)
combining equations to eliminate \(g(4)\) (M1)
eg\(\;\;\;g(5) – [\ln 3 – 0.66] = 0.21\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 3
attempt to set up a definite integral (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x = – 0.66 + 0.21,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } \)
correct working (A1)
eg\(\;\;\;g(5) – g(2) = – 0.45\)
correct substitution (A1)
eg\(\;\;\;g(5) – \ln 3 = – 0.45\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
[4 marks]
Total [16 marks]
Question
A particle P starts from a point A and moves along a horizontal straight line. Its velocity \(v{\text{ cm}}\,{{\text{s}}^{ – 1}}\) after \(t\) seconds is given by
\[v(t) = \left\{ {\begin{array}{*{20}{l}} { – 2t + 2,}&{{\text{for }}0 \leqslant t \leqslant 1} \\ {3\sqrt t + \frac{4}{{{t^2}}} – 7,}&{{\text{for }}1 \leqslant t \leqslant 12} \end{array}} \right.\]
The following diagram shows the graph of \(v\).
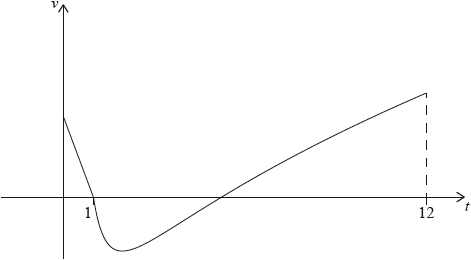
P is at rest when \(t = 1\) and \(t = p\).
When \(t = q\), the acceleration of P is zero.
Find the initial velocity of \(P\).
Find the value of \(p\).
(i) Find the value of \(q\).
(ii) Hence, find the speed of P when \(t = q\).
(i) Find the total distance travelled by P between \(t = 1\) and \(t = p\).
(ii) Hence or otherwise, find the displacement of P from A when \(t = p\).
Answer/Explanation
Markscheme
valid attempt to substitute \(t = 0\) into the correct function (M1)
eg\(\,\,\,\,\,\)\( – 2(0) + 2\)
2 A1 N2
[2 marks]
recognizing \(v = 0\) when P is at rest (M1)
5.21834
\(p = 5.22{\text{ }}({\text{seconds}})\) A1 N2
[2 marks]
(i) recognizing that \(a = v’\) (M1)
eg\(\,\,\,\,\,\)\(v’ = 0\), minimum on graph
1.95343
\(q = 1.95\) A1 N2
(ii) valid approach to find their minimum (M1)
eg\(\,\,\,\,\,\)\(v(q),{\text{ }} – 1.75879\), reference to min on graph
1.75879
speed \( = 1.76{\text{ }}(c\,{\text{m}}\,{{\text{s}}^{ – 1}})\) A1 N2
[4 marks]
(i) substitution of correct \(v(t)\) into distance formula, (A1)
eg\(\,\,\,\,\,\)\(\int_1^p {\left| {3\sqrt t + \frac{4}{{{t^2}}} – 7} \right|{\text{d}}t,{\text{ }}\left| {\int {3\sqrt t + \frac{4}{{{t^2}}} – 7{\text{d}}t} } \right|} \)
4.45368
distance \( = 4.45{\text{ }}({\text{cm}})\) A1 N2
(ii) displacement from \(t = 1\) to \(t = p\) (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\( – 4.45368,{\text{ }}\int_1^p {\left( {3\sqrt t + \frac{4}{{{t^2}}} – 7} \right){\text{d}}t} \)
displacement from \(t = 0\) to \(t = 1\) (A1)
eg\(\,\,\,\,\,\)\(\int_0^1 {( – 2t + 2){\text{d}}t,{\text{ }}0.5 \times 1 \times 2,{\text{ 1}}} \)
valid approach to find displacement for \(0 \leqslant t \leqslant p\) M1
eg\(\,\,\,\,\,\)\(\int_0^1 {( – 2t + 2){\text{d}}t + \int_1^p {\left( {3\sqrt t + \frac{4}{{{t^2}}} – 7} \right){\text{d}}t,{\text{ }}\int_0^1 {( – 2t + 2){\text{d}}t – 4.45} } } \)
\( – 3.45368\)
displacement \( = – 3.45{\text{ }}({\text{cm}})\) A1 N2
[6 marks]
Question
Let \(f(x) = 6 – \ln ({x^2} + 2)\), for \(x \in \mathbb{R}\). The graph of \(f\) passes through the point \((p,{\text{ }}4)\), where \(p > 0\).
Find the value of \(p\).
The following diagram shows part of the graph of \(f\).
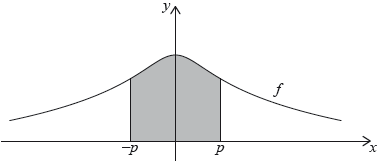
The region enclosed by the graph of \(f\), the \(x\)-axis and the lines \(x = – p\) and \(x = p\) is rotated 360° about the \(x\)-axis. Find the volume of the solid formed.
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(f(p) = 4\), intersection with \(y = 4,{\text{ }} \pm 2.32\)
2.32143
\(p = \sqrt {{{\text{e}}^2} – 2} \) (exact), 2.32 A1 N2
[2 marks]
attempt to substitute either their limits or the function into volume formula (must involve \({f^2}\), accept reversed limits and absence of \(\pi \) and/or \({\text{d}}x\), but do not accept any other errors) (M1)
eg\(\,\,\,\,\,\)\(\int_{ – 2.32}^{2.32} {{f^2},{\text{ }}\pi \int {{{\left( {6 – \ln ({x^2} + 2)} \right)}^2}{\text{d}}x,{\text{ 105.675}}} } \)
331.989
\({\text{volume}} = 332\) A2 N3
[3 marks]
Question
A particle P moves along a straight line. The velocity v m s−1 of P after t seconds is given by v (t) = 7 cos t − 5t cos t, for 0 ≤ t ≤ 7.
The following diagram shows the graph of v.
Find the initial velocity of P.
Find the maximum speed of P.
Write down the number of times that the acceleration of P is 0 m s−2 .
Find the acceleration of P when it changes direction.
Find the total distance travelled by P.
Answer/Explanation
Markscheme
initial velocity when t = 0 (M1)
eg v(0)
v = 17 (m s−1) A1 N2
[2 marks]
recognizing maximum speed when \(\left| v \right|\) is greatest (M1)
eg minimum, maximum, v’ = 0
one correct coordinate for minimum (A1)
eg 6.37896, −24.6571
24.7 (ms−1) A1 N2
[3 marks]
recognizing a = v ′ (M1)
eg \(a = \frac{{{\text{d}}v}}{{{\text{d}}t}}\), correct derivative of first term
identifying when a = 0 (M1)
eg turning points of v, t-intercepts of v ′
3 A1 N3
[3 marks]
recognizing P changes direction when v = 0 (M1)
t = 0.863851 (A1)
−9.24689
a = −9.25 (ms−2) A2 N3
[4 marks]
correct substitution of limits or function into formula (A1)
eg \(\int_0^7 {\left| {\,v\,} \right|,\,\int_0^{0.8638} {v{\text{d}}t – \int_{0.8638}^7 {v{\text{d}}t} } ,\,\,\int {\left| {\,7\,{\text{cos}}\,x – 5{x^{{\text{cos}}\,x}}\,} \right|} \,dx,\,\,3.32 = 60.6} \)
63.8874
63.9 (metres) A2 N3
[3 marks]
Question
Let \(h(x) = \frac{{2x – 1}}{{x + 1}}\) , \(x \ne – 1\) .
Find \({h^{ – 1}}(x)\) .
(i) Sketch the graph of h for \( – 4 \le x \le 4\) and \( – 5 \le y \le 8\) , including any asymptotes.
(ii) Write down the equations of the asymptotes.
(iii) Write down the x-intercept of the graph of h .
Let R be the region in the first quadrant enclosed by the graph of h , the x-axis and the line \(x = 3\).
(i) Find the area of R.
(ii) Write down an expression for the volume obtained when R is revolved through \({360^ \circ }\) about the x-axis.
Answer/Explanation
Markscheme
\(y = \frac{{2x – 1}}{{x + 1}}\)
interchanging x and y (seen anywhere) M1
e.g. \(x = \frac{{2y – 1}}{{y + 1}}\)
correct working A1
e.g. \(xy + x = 2y – 1\)
collecting terms A1
e.g. \(x + 1 = 2y – xy\) , \(x + 1 = y(2 – x)\)
\({h^{ – 1}}(x) = \frac{{x + 1}}{{2 – x}}\) A1 N2
[4 marks]
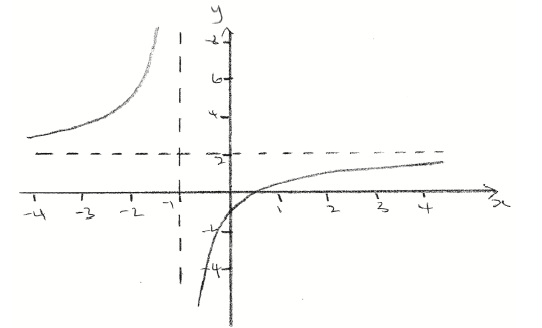A1A1A1A1 N4
Note: Award A1 for approximately correct intercepts, A1 for correct shape, A1 for asymptotes, A1 for approximately correct domain and range.
(ii) \(x = – 1\) , \(y = 2\) A1A1 N2
(iii) \(\frac{1}{2}\) A1 N1
[7 marks]
(i) \({\text{area}} = 2.06\) A2 N2
(ii) attempt to substitute into volume formula (do not accept \(\pi \int_a^b {{y^2}{\rm{d}}x} \) ) M1
volume \( = \pi {\int_{\frac{1}{2}}^3 {\left( {\frac{{2x – 1}}{{x + 1}}} \right)} ^2}{\rm{d}}x\) A2 N3
[5 marks]