Question
The acceleration, \(a{\text{ m}}{{\text{s}}^{ – 2}}\), of a particle at time t seconds is given by \(a = 2t + \cos t\) .
Find the acceleration of the particle at \(t = 0\) .
Find the velocity, v, at time t, given that the initial velocity of the particle is \({\text{m}}{{\text{s}}^{ – 1}}\) .
Find \(\int_0^3 {v{\rm{d}}t} \) , giving your answer in the form \(p – q\cos 3\) .
What information does the answer to part (c) give about the motion of the particle?
Answer/Explanation
Markscheme
substituting \(t = 0\) (M1)
e.g. \(a(0) = 0 + \cos 0\)
\(a(0) = 1\) A1 N2
[2 marks]
evidence of integrating the acceleration function (M1)
e.g. \(\int {(2t + \cos t){\text{d}}t} \)
correct expression \({t^2} + \sin t + c\) A1A1
Note: If “\( + c\)” is omitted, award no further marks.
evidence of substituting (2,0) into indefinite integral (M1)
e.g. \(2 = 0 + \sin 0 + c\) , \(c = 2\)
\(v(t) = {t^2} + \sin t + 2\) A1 N3
[5 marks]
\(\int {({t^2} + \sin t + 2)} {\rm{d}}t = \frac{{{t^3}}}{3} – \cos t + 2t\) A1A1A1
Note: Award A1 for each correct term.
evidence of using \(v(3) – v(0)\) (M1)
correct substitution A1
e.g. \((9 – \cos 3 + 6) – (0 – \cos 0 + 0)\) , \((15 – \cos 3) – ( – 1)\)
\(16 – \cos 3\) (accept \(p = 16\) , \(q = – 1\) ) A1A1 N3
[7 marks]
reference to motion, reference to first 3 seconds R1R1 N2
e.g. displacement in 3 seconds, distance travelled in 3 seconds
[2 marks]
Question
The velocity v ms−1 of a particle at time t seconds, is given by \(v = 2t + \cos 2t\) , for \(0 \le t \le 2\) .
Write down the velocity of the particle when \(t = 0\) .
When \(t = k\) , the acceleration is zero.
(i) Show that \(k = \frac{\pi }{4}\) .
(ii) Find the exact velocity when \(t = \frac{\pi }{4}\) .
When \(t < \frac{\pi }{4}\) , \(\frac{{{\rm{d}}v}}{{{\rm{d}}t}} > 0\) and when \(t > \frac{\pi }{4}\) , \(\frac{{{\rm{d}}v}}{{{\rm{d}}t}} > 0\) .
Sketch a graph of v against t .
Let d be the distance travelled by the particle for \(0 \le t \le 1\) .
(i) Write down an expression for d .
(ii) Represent d on your sketch.
Answer/Explanation
Markscheme
\(v = 1\) A1 N1
[1 mark]
(i) \(\frac{{\rm{d}}}{{{\rm{d}}t}}(2t) = 2\) A1
\(\frac{{\rm{d}}}{{{\rm{d}}t}}(\cos 2t) = – 2\sin 2t\) A1A1
Note: Award A1 for coefficient 2 and A1 for \( – \sin 2t\) .
evidence of considering acceleration = 0 (M1)
e.g. \(\frac{{{\rm{d}}v}}{{{\rm{d}}t}} = 0\) , \(2 – 2\sin 2t = 0\)
correct manipulation A1
e.g. \(\sin 2k = 1\) , \(\sin 2t = 1\)
\(2k = \frac{\pi }{2}\) (accept \(2t = \frac{\pi }{2}\) ) A1
\(k = \frac{\pi }{4}\) AG N0
(ii) attempt to substitute \(t = \frac{\pi }{4}\) into v (M1)
e.g. \(2\left( {\frac{\pi }{4}} \right) + \cos \left( {\frac{{2\pi }}{4}} \right)\)
\(v = \frac{\pi }{2}\) A1 N2
[8 marks]
 A1A1A2 N4
A1A1A2 N4
Notes: Award A1 for y-intercept at \((0{\text{, }}1)\) , A1 for curve having zero gradient at \(t = \frac{\pi }{4}\) , A2 for shape that is concave down to the left of \(\frac{\pi }{4}\) and concave up to the right of \(\frac{\pi }{4}\) . If a correct curve is drawn without indicating \(t = \frac{\pi }{4}\) , do not award the second A1 for the zero gradient, but award the final A2 if appropriate. Sketch need not be drawn to scale. Only essential features need to be clear.
[4 marks]
(i) correct expression A2
e.g. \(\int_0^1 {(2t + \cos 2t){\rm{d}}t} \) , \(\left[ {{t^2} + \frac{{\sin 2t}}{2}} \right]_0^1\) , \(1 + \frac{{\sin 2}}{2}\) , \(\int_0^1 {v{\rm{d}}t} \)
(ii)
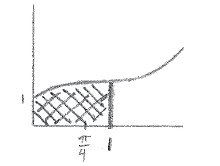 A1
A1
Note: The line at \(t = 1\) needs to be clearly after \(t = \frac{\pi }{4}\) .
[3 marks]
Question
In this question, you are given that \(\cos \frac{\pi }{3} = \frac{1}{2}\) , and \(\sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\) .
The displacement of an object from a fixed point, O is given by \(s(t) = t – \sin 2t\) for \(0 \le t \le \pi \) .
Find \(s'(t)\) .
In this interval, there are only two values of t for which the object is not moving. One value is \(t = \frac{\pi }{6}\) .
Find the other value.
Show that \(s'(t) > 0\) between these two values of t .
Find the distance travelled between these two values of t .
Answer/Explanation
Markscheme
\(s'(t) = 1 – 2\cos 2t\) A1A2 N3
Note: Award A1 for 1, A2 for \(- 2\cos 2t\) .
[3 marks]
evidence of valid approach (M1)
e.g. setting \(s'(t) = 0\)
correct working A1
e.g. \(2\cos 2t = 1\) , \(\cos 2t = \frac{1}{2}\)
\(2t = \frac{\pi }{3}\) , \(\frac{{5\pi }}{3}\) , \(\ldots \) (A1)
\(t = \frac{{5\pi }}{6}\) A1 N3
[4 marks]
evidence of valid approach (M1)
e.g. choosing a value in the interval \(\frac{\pi }{6} < t < \frac{{5\pi }}{6}\)
correct substitution A1
e.g. \(s’\left( {\frac{\pi }{2}} \right) = 1 – 2\cos \pi \)
\(s’\left( {\frac{\pi }{2}} \right) = 3\) A1
\(s'(t) > 0\) AG N0
[3 marks]
evidence of approach using s or integral of \(s’\) (M1)
e.g. \(\int {s'(t){\rm{d}}t} \) ; \(s\left( {\frac{{5\pi }}{6}} \right)\) , \(s\left( {\frac{\pi }{6}} \right)\) ; \(\left[ {t – \sin 2t} \right]_{\frac{\pi }{6}}^{\frac{{5\pi }}{6}}\)
substituting values and subtracting (M1)
e.g. \(s\left( {\frac{{5\pi }}{6}} \right) – s\left( {\frac{\pi }{6}} \right)\) , \(\left( {\frac{\pi }{6} – \frac{{\sqrt 3 }}{2}} \right) – \left( {\frac{{5\pi }}{6} – \left( { – \frac{{\sqrt 3 }}{2}} \right)} \right)\)
correct substitution A1
e.g. \(\frac{{5\pi }}{6} – \sin \frac{{5\pi }}{3} – \left[ {\frac{\pi }{6} – \sin \frac{\pi }{3}} \right]\) , \(\left( {\frac{{5\pi }}{6} – \left( { – \frac{{\sqrt 3 }}{2}} \right)} \right) – \left( {\frac{\pi }{6} – \frac{{\sqrt 3 }}{2}} \right)\)
distance is \(\frac{{2\pi }}{3} + \sqrt 3 \) A1A1 N3
Note: Award A1 for \(\frac{{2\pi }}{3}\) , A1 for \(\sqrt 3 \) .
[5 marks]
