Question
In a game there are n players, where \(n > 2\) . Each player has a disc, one side of which is red and one side blue. When thrown, the disc is equally likely to show red or blue. All players throw their discs simultaneously. A player wins if his disc shows a different colour from all the other discs. Players throw repeatedly until one player wins.
Let X be the number of throws each player makes, up to and including the one on which the game is won.
(a) State the distribution of X .
(b) Find \({\text{P}}(X = x)\) in terms of n and x .
(c) Find \({\text{E}}(X)\) in terms of n .
(d) Given that n = 7 , find the least number, k , such that \({\text{P}}(X \leqslant k) > 0.5\) .
▶️Answer/Explanation
Markscheme
(a) geometric distribution A1
[1 mark]
(b) let R be the event throwing the disc and it landing on red and
let B be the event throwing the disc and it landing on blue
\({\text{P}}(X = 1) = p = {\text{P}}\left( {1B{\text{ and }}(n – 1)R{\text{ or }}1R{\text{ and }}(n – 1)B} \right)\) (M1)
\( = n \times \frac{1}{2} \times {\left( {\frac{1}{2}} \right)^{n – 1}} + n \times \frac{1}{2} \times {\left( {\frac{1}{2}} \right)^{n – 1}}\) (A1)
\( = \frac{n}{{{2^{n – 1}}}}\) A1
hence \({\text{P}}(X = x) = \frac{n}{{{2^{n – 1}}}}{\left( {1 – \frac{n}{{{2^{n – 1}}}}} \right)^{x – 1}},{\text{ }}(x \geqslant 1)\) A1
Notes: \(x \geqslant 1\) not required for final A1.
Allow FT for final A1.
[4 marks]
(c) \({\text{E}}(X) = \frac{1}{p}\)
\( = \frac{{{2^{n – 1}}}}{n}\) A1
[1 mark]
(d) when \(n = 7\) , \({\text{P}}(X = x) = {\left( {1 – \frac{7}{{64}}} \right)^{x – 1}} \times \frac{7}{{64}}\) (M1)
\( = \frac{7}{{64}} \times {\left( {\frac{{57}}{{64}}} \right)^{x – 1}}\)
\({\text{P}}(X \leqslant k) = \sum\limits_{x = 1}^k {\frac{7}{{64}} \times {{\left( {\frac{{57}}{{64}}} \right)}^{x – 1}}} \) (M1)(A1)
\( \Rightarrow \frac{7}{{64}} \times \frac{{1 – {{\left( {\frac{{57}}{{64}}} \right)}^k}}}{{1 – \frac{{57}}{{64}}}} > 0.5\) (M1)(A1)
\( \Rightarrow 1 – {\left( {\frac{{57}}{{64}}} \right)^k} > 0.5\)
\( \Rightarrow {\left( {\frac{{57}}{{64}}} \right)^k} < 0.5\)
\( \Rightarrow k > \frac{{\log 0.5}}{{\log \frac{{57}}{{64}}}}\) (M1)
\( \Rightarrow k > 5.98\) (A1)
\( \Rightarrow k = 6\) A1
Note: Tabular and other GDC methods are acceptable.
[8 marks]
Total [14 marks]
Examiners report
This question was found difficult by the majority of candidates and few fully correct answers were seen. Few candidates were able to find \({\text{P}}(X = x)\) in terms of n and x and many did not realise that the last part of the question required them to find the sum of a series. However, better candidates received over 75% of the marks because the answers could be followed through.
Question
The random variable X has a geometric distribution with parameter p .
a.Show that \({\text{P}}(X \leqslant n) = 1 – {(1 – p)^n},{\text{ }}n \in {\mathbb{Z}^ + }\) .[3]
b.Deduce an expression for \({\text{P}}(m < X \leqslant n)\,,{\text{ }}m\,,{\text{ }}n \in {\mathbb{Z}^ + }\) and m < n .[1]
c.Given that p = 0.2, find the least value of n for which \({\text{P}}(1 < X \leqslant n) > 0.5\,,{\text{ }}n \in {\mathbb{Z}^ + }\) .[2]
▶️Answer/Explanation
Markscheme
\({\text{P}}(X \leqslant n) = \sum\limits_{{\text{i}} = 1}^n {{\text{P}}(X = {\text{i}}) = \sum\limits_{{\text{i}} = 1}^n {p{q^{{\text{i}} – 1}}} } \) M1A1
\( = p\frac{{1 – {q^n}}}{{1 – q}}\) A1
\( = 1 – {(1 – p)^n}\) AG
[3 marks]
\({(1 – p)^m} – {(1 – p)^n}\) A1
[1 mark]
attempt to solve \(0.8 – {(0.8)^n} > 0.5\) M1
obtain n = 6 A1
[2 marks]
Question
Jenny and her Dad frequently play a board game. Before she can start Jenny has to throw a “six” on an ordinary six-sided dice. Let the random variable X denote the number of times Jenny has to throw the dice in total until she obtains her first “six”.
a.If the dice is fair, write down the distribution of X , including the value of any parameter(s).[1]
b.Write down E(X ) for the distribution in part (a).[1]
d.Before Jenny’s Dad can start, he has to throw two “sixes” using a fair, ordinary six-sided dice. Let the random variable Y denote the total number of times Jenny’s Dad has to throw the dice until he obtains his second “six”.
Write down the distribution of Y , including the value of any parameter(s).[1]
e.Before Jenny’s Dad can start, he has to throw two “sixes” using a fair, ordinary six-sided dice. Let the random variable Y denote the total number of times Jenny’s Dad has to throw the dice until he obtains his second “six”.
Find the value of y such that \({\text{P}}(Y = y) = \frac{1}{{36}}\).[1]
f.Before Jenny’s Dad can start, he has to throw two “sixes” using a fair, ordinary six-sided dice. Let the random variable Y denote the total number of times Jenny’s Dad has to throw the dice until he obtains his second “six”.
Find \({\text{P}}(Y \leqslant 6)\) .[2]
▶️Answer/Explanation
Markscheme
\(X \sim {\text{Geo}}\left( {\frac{1}{6}} \right){\text{ or NB}}\left( {1,\frac{1}{6}} \right)\) A1
[1 mark]
\({\text{E}}(X) = 6\) A1
[1 mark]
Y is \({\text{NB}}\left( {2,\frac{1}{6}} \right)\) A1
[1 mark]
\({\text{P}}(Y = y) = \frac{1}{{36}}{\text{ gives }}y = 2\) A1
(as all other probabilities would have a factor of 5 in the numerator)
[1 mark]
\({\text{P}}(Y \leqslant 6) = {\left( {\frac{1}{6}} \right)^2} + 2\left( {\frac{5}{6}} \right){\left( {\frac{1}{6}} \right)^2} + 3{\left( {\frac{5}{6}} \right)^2}{\left( {\frac{1}{6}} \right)^2} + 4{\left( {\frac{5}{6}} \right)^3}{\left( {\frac{1}{6}} \right)^2} + 5{\left( {\frac{5}{6}} \right)^4}{\left( {\frac{1}{6}} \right)^2}\) (M1)
\( = 0.263\) A1
[2 marks]
Question
Consider the random variable \(X \sim {\text{Geo}}(p)\).
(a) State \({\text{P}}(X < 4)\).
(b) Show that the probability generating function for X is given by \({G_X}(t) = \frac{{pt}}{{1 – qt}}\), where \(q = 1 – p\).
Let the random variable \(Y = 2X\).
(c) (i) Show that the probability generating function for Y is given by \({G_Y}(t) = {G_X}({t^2})\).
(ii) By considering \({G’_Y}(1)\), show that \({\text{E}}(Y) = 2{\text{E}}(X)\).
Let the random variable \(W = 2X + 1\).
(d) (i) Find the probability generating function for W in terms of the probability generating function of Y.
(ii) Hence, show that \({\text{E}}(W) = 2{\text{E}}(X) + 1\).
▶️Answer/Explanation
Markscheme
(a) use of \({\text{P}}(X = n) = p{q^{n – 1}}{\text{ }}(q = 1 – p)\) (M1)
\({\text{P}}(X < 4) = p + pq + p{q^2}{\text{ }}\left( { = 1 – {q^3}} \right){\text{ }}\left( { = 1 – {{(1 – p)}^3}} \right){\text{ }}( = 3p – 3{p^2} + {p^3})\) A1
[2 marks]
(b) \({G_X}(t) = {\text{P}}(X = 1)t + {\text{P}}(X = 2){t^2} + \ldots \) (M1)
\( = pt + pq{t^2} + p{q^2}{t^3} + \ldots \) A1
summing an infinite geometric series M1
\( = \frac{{pt}}{{1 – qt}}\) AG
[3 marks]
(c) (i) EITHER
\({G_Y}(t) = {\text{P}}(Y = 1)t + {\text{P}}(Y = 2){t^2} + \ldots \) A1
\( = 0 \times t + {\text{P}}(X = 1){t^2} + 0 \times {t^3} + {\text{P}}(X = 2){t^4} + \ldots \) M1A1
\( = {G_X}({t^2})\) AG
OR
\({G_Y}(t) = E({t^Y}) = E({t^{2X}})\) M1A1
\( = E\left( {{{({t^2})}^X}} \right)\) A1
\( = {G_X}({t^2})\) AG
(ii) \({\text{E}}(Y) = {G’_Y}(1)\) A1
EITHER
\( = 2t{G’_X}({t^2})\) evaluated at \(t = 1\) M1A1
\( = 2{\text{E}}(X)\) AG
OR
\( = \frac{{\text{d}}}{{{\text{d}}x}}\left( {\frac{{p{t^2}}}{{(1 – q{t^2})}}} \right) = \frac{{2pt(1 – q{t^2}) + 2pq{t^3}}}{{{{(1 – q{t^2})}^2}}}\) evaluated at \(t = 1\) A1
\( = 2 \times \frac{{p(1 – qt) + pqt}}{{{{(1 – qt)}^2}}}\) evaluated at \(t = 1{\text{ (or }}\frac{2}{p})\) A1
\( = 2{\text{E}}(X)\) AG
[6 marks]
(d) (i) \({G_W}(t) = t{G_Y}(t)\) (or equivalent) A2
(ii) attempt to evaluate \({G’_W}(t)\) M1
EITHER
obtain \(1 \times {G_Y}(t) + t \times {G’_Y}(t)\) A1
substitute \(t = 1\) to obtain \(1 \times 1 + 1 \times {G’_Y}(1)\) A1
OR
\( = \frac{{\text{d}}}{{{\text{d}}x}}\left( {\frac{{p{t^3}}}{{(1 – q{t^2})}}} \right) = \frac{{3p{t^2}(1 – q{t^2}) + 2pq{t^4}}}{{{{(1 – q{t^2})}^2}}}\) A1
substitute \(t = 1\) to obtain \(1 + \frac{2}{p}\) A1
\( = 1 + 2{\text{E}}(X)\) AG
[5 marks]
Total [16 marks]
Examiners report
Question
A continuous random variable \(T\) has a probability density function defined by
\(f(t) = \left\{ {\begin{array}{*{20}{c}} {\frac{{t(4 – {t^2})}}{4}}&{0 \leqslant t \leqslant 2} \\ {0,}&{{\text{otherwise}}} \end{array}} \right.\).
a.Find the cumulative distribution function \(F(t)\), for \(0 \leqslant t \leqslant 2\).[3]
b.i.Sketch the graph of \(F(t)\) for \(0 \leqslant t \leqslant 2\), clearly indicating the coordinates of the endpoints.[2]
b.ii.Given that \(P(T < a) = 0.75\), find the value of \(a\).[2]
▶️Answer/Explanation
Markscheme
\(F(t) = \int_0^t {\left( {x – \frac{{{x^3}}}{4}} \right){\text{d}}x{\text{ }}\left( { = \int_0^t {\frac{{x(4 – {x^2})}}{4}{\text{d}}x} } \right)} \) M1
\( = \left[ {\frac{{{x^2}}}{2} – \frac{{{x^4}}}{{16}}} \right]_0^t{\text{ }}\left( { = \left[ {\frac{{{x^2}(8 – {x^2})}}{{16}}} \right]_0^t} \right){\text{ }}\left( { = \left[ {\frac{{ – 4 – {x^2}{)^2}}}{{16}}} \right]_0^t} \right)\) A1
\( = \frac{{{t^2}}}{2} – \frac{{{t^4}}}{{16}}{\text{ }}\left( { = \frac{{{t^2}(8 – {t^2})}}{{16}}} \right){\text{ }}\left( { = 1 – \frac{{{{(4 – {t^2})}^2}}}{{16}}} \right)\) A1
Note: Condone integration involving \(t\) only.
Note: Award M1A0A0 for integration without limits eg, \(\int {\frac{{t(4 – {t^2})}}{4}{\text{d}}t = \frac{{{t^2}}}{2} – \frac{{{t^4}}}{{16}}} \) or equivalent.
Note: But allow integration \( + \) \(C\) then showing \(C = 0\) or even integration without \(C\) if \(F(0) = 0\) or \(F(2) = 1\) is confirmed.
[3 marks]
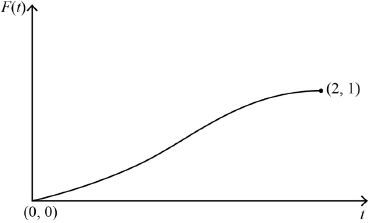
correct shape including correct concavity A1
clearly indicating starts at origin and ends at \((2,{\text{ }}1)\) A1
Note: Condone the absence of \((0,{\text{ }}0)\).
Note: Accept 2 on the \(x\)-axis and 1 on the \(y\)-axis correctly placed.
[2 marks]
attempt to solve \(\frac{{{a^2}}}{2} – \frac{{{a^4}}}{{16}} = 0.75\) (or equivalent) for \(a\) (M1)
\(a = 1.41{\text{ }}( = \sqrt 2 )\) A1
Note: Accept any answer that rounds to 1.4.
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
Consider an unbiased tetrahedral (four-sided) die with faces labelled 1, 2, 3 and 4 respectively.
The random variable X represents the number of throws required to obtain a 1.
a.State the distribution of X.[1]
b.Show that the probability generating function, \(G\left( t \right)\), for X is given by \(G\left( t \right) = \frac{t}{{4 – 3t}}\).[4]
c.Find \(G’\left( t \right)\).[2]
d.Determine the mean number of throws required to obtain a 1.[1]
▶️Answer/Explanation
Markscheme
X is geometric (or negative binomial) A1
[1 mark]
\(G\left( t \right) = \frac{1}{4}t + \frac{1}{4}\left( {\frac{3}{4}} \right){t^2} + \frac{1}{4}{\left( {\frac{3}{4}} \right)^2}{t^3} + \ldots \) M1A1
recognition of GP \(\left( {{u_1} = \frac{1}{4}t,\,\,r = \frac{3}{4}t} \right)\) (M1)
\( = \frac{{\frac{1}{4}t}}{{1 – \frac{3}{4}t}}\) A1
leading to \(G\left( t \right) = \frac{t}{{4 – 3t}}\) AG
[4 marks]
attempt to use product or quotient rule M1
\(G’\left( t \right) = \frac{4}{{{{\left( {4 – 3t} \right)}^2}}}\) A1
[2 marks]
4 A1
Note: Award A1FT to a candidate that correctly calculates the value of \(G’\left( 1 \right)\) from their \(G’\left( t \right)\).
[1 mark]
